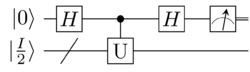
One Clean Qubit
The One Clean Qubit model of computation is performed an
Error Bounds and Composability
The most standard definition of DQC1 requires that measuring the output qubit correctly accepts or rejects the input, with error at most
DQC1 does not admit an obvious notion of parallel composability or amplification: there is no clear construction to transform a circuit with, say, a (2/5,3/5) acceptance gap into a more accurate (1/5,4/5) acceptance gap.
It is known that DQC1 offers composability in the sense that the "one" clean qubit can be upgraded to "two" clean qubits, or even
Relation to other classes
Because as many as
It is known that simulating the sampling problem even for 3 output qubits is classically hard, in the sense that it would imply a PH collapse.[5]
The term DQC1 has been used to instead refer to decision problems solved by a polynomial time classical circuit that adaptively makes queries to polynomially many DQC1 circuits.[6] In this sense of use, the class naturally contains all of BPP, and the power of the class is focused on the "inherently quantum" power.
Trace Estimation
Trace estimation is complete for DQC1.[7] Let
DQC1-complete Problems
In addition to unitary trace estimation, estimating a coefficient in the Pauli decomposition of a unitary and approximating the Jones polynomial at a fifth root of unity are also DQC1-complete. In fact, trace estimation is a special case of Pauli decomposition coefficient estimation.[8]
References
- ↑ Knill, Emanuel; Laflamme, Raymond Laflamme (1998). "Power of One Bit of Quantum Information". Physical Review Letters 81 (25): 5672–5675. doi:10.1103/PhysRevLett.81.5672. Bibcode: 1998PhRvL..81.5672K.
- ↑ Jump up to: 2.0 2.1 Peter W. Shor (2008). "Estimating Jones polynomials is a complete problem for one clean qubit". Quantum Information & Computation 8 (8&9): 681–714. doi:10.26421/QIC8.8-9-1.
- ↑ Jump up to: 3.0 3.1 Shepherd, Dan (2006). "Computation with Unitaries and One Pure Qubit". arXiv:quant-ph/0608132.
- ↑ Shepherd's paper adopts the nonstandard notation of DQC1 referring only to the circuits and sampling problems, and use BQ1P to refer to decision problems.
- ↑ Morimae, Tomoyuki; Fujii, Keisuke; Fitzsimons, Joseph F. (2014). "Hardness of Classically Simulating the One-Clean-Qubit Model". Physical Review Letters 112 (13): 130502. doi:10.1103/PhysRevLett.112.130502. PMID 24745398. Bibcode: 2014PhRvL.112m0502M. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.112.130502.
- ↑ Chowdhury, Anirban N.; Somma, Rolando D.; Subaşı, Yiğit (2021). "Computing partition functions in the one-clean-qubit model". Physical Review A 103 (3): 032422. doi:10.1103/PhysRevA.103.032422. Bibcode: 2021PhRvA.103c2422C. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.103.032422.
- ↑ Shepherd, Dan (2006). "Computation with Unitaries and One Pure Qubit". arXiv:quant-ph/0608132.
- ↑ Cade, Chris; Montanaro, Ashley (2017). "The Quantum Complexity of Computing Schatten p-norms". arXiv:1706.09279 [quant-ph].
 |