Physics:Sznajd model

Sketch of the 2 updating rules, social validation (top panel) and discord destroys (bottom panel), assuming that the two men in the middle have been chosen to be updated. Without loss of generality, red men (looking to the left) say no, blue men (looking to the right) say yes. The purple men can have either opinion.

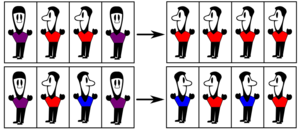
The Sznajd model or United we stand, divided we fall (USDF) model is a sociophysics model introduced in 2000 to gain fundamental understanding about opinion dynamics. The Sznajd model implements a phenomenon called social validation and thus extends the Ising spin model. In simple words, the model states:

• Social validation: If two people share the same opinion, their neighbors will start to agree with them.
• Discord destroys: If a block of adjacent persons disagree, their neighbors start to argue with them.

Mathematical formulation

For simplicity, one assumes that each individual [math]\displaystyle{ i }[/math] has an opinion S_i which might be Boolean ([math]\displaystyle{ S_i=-1 }[/math] for no, [math]\displaystyle{ S_i=1 }[/math] for yes) in its simplest formulation, which means that each individual either agrees or disagrees to a given question.

In the original 1D-formulation, each individual has exactly two neighbors just like beads on a bracelet. At each time step a pair of individual [math]\displaystyle{ S_i }[/math] and [math]\displaystyle{ S_{i+1} }[/math] is chosen at random to change their nearest neighbors' opinion (or: Ising spins) [math]\displaystyle{ S_{i-1} }[/math] and [math]\displaystyle{ S_{i+2} }[/math] according to two dynamical rules:

1. If [math]\displaystyle{ S_i=S_{i+1} }[/math] then [math]\displaystyle{ S_{i-1}=S_i }[/math] and [math]\displaystyle{ S_{i+2}=S_i }[/math]. This models social validation, if two people share the same opinion, their neighbors will change their opinion.
2. If [math]\displaystyle{ S_i=-S_{i+1} }[/math] then [math]\displaystyle{ S_{i-1}=S_{i+1} }[/math] and [math]\displaystyle{ S_{i+2}=S_i }[/math]. Intuitively: If the given pair of people disagrees, both adopt the opinion of their other neighbor.

Findings for the original formulations

In a closed (1 dimensional) community, two steady states are always reached, namely complete consensus (which is called ferromagnetic state in physics) or stalemate (the antiferromagnetic state). Furthermore, Monte Carlo simulations showed that these simple rules lead to complicated dynamics, in particular to a power law in the decision time distribution with an exponent of -1.5.

Modifications

The final (antiferromagnetic) state of alternating all-on and all-off is unrealistic to represent the behavior of a community. It would mean that the complete population uniformly changes their opinion from one time step to the next. For this reason an alternative dynamical rule was proposed. One possibility is that two spins [math]\displaystyle{ S_i }[/math] and [math]\displaystyle{ S_{i+1} }[/math] change their nearest neighbors according to the two following rules:

1. Social validation remains unchanged: If [math]\displaystyle{ S_i=S_{i+1} }[/math] then [math]\displaystyle{ S_{i-1}=S_{i} }[/math] and [math]\displaystyle{ S_{i+2}=S_{i} }[/math].
2. If [math]\displaystyle{ S_i=-S_{i+1} }[/math] then [math]\displaystyle{ S_{i-1}=S_{i} }[/math] and [math]\displaystyle{ S_{i+2}=S_{i+1} }[/math]

Relevance

In recent years, statistical physics has been accepted as modeling framework for phenomena outside the traditional physics. Fields as econophysics or sociophysics formed, and many quantitative analysts in finance are physicists. The Ising model in statistical physics has been a very important step in the history of studying collective (critical) phenomena. The Sznajd model is a simple but yet important variation of prototypical Ising system.

In 2007, Katarzyna Sznajd-Weron has been recognized by the Young Scientist Award for Socio- and Econophysics of the Deutsche Physikalische Gesellschaft (German Physical Society) for an outstanding original contribution using physical methods to develop a better understanding of socio-economic problems.

Applications

The Sznajd model belongs to the class of binary-state dynamics on a networks also referred to as Boolean networks. This class of systems includes the Ising model, the voter model and the q-voter model, the Bass diffusion model, threshold models and others. The Sznajd model can be applied to various fields:

• The finance interpretation considers the spin-state [math]\displaystyle{ S_i=1 }[/math] as a bullish trader placing orders, whereas a [math]\displaystyle{ S_i=0 }[/math] would correspond to a trader who is bearish and places sell orders.

External links

• Katarzyna Sznajd-Weron currently works at the Wrocław University of Technology performing research on interdisciplinary applications of statistical physics, complex systems, critical phenomena, sociophysics and agent-based modeling.