Physics:Debye model
This article reads like a textbook and may require cleanup. Please help to improve this article to make it neutral in tone and meet Wikipedia's quality standards. (January 2024) |
Template:Needs more references
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat (heat capacity) in a solid.[1] It treats the vibrations of the atomic lattice (heat) as phonons in a box in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to [math]\displaystyle{ T^3 }[/math][clarification needed] – the Debye T 3 law. Similarly to the Einstein photoelectron model, it recovers the Dulong–Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures[clarification needed].
Derivation
The Debye model is a solid-state equivalent of Planck's law of black body radiation, which treats electromagnetic radiation as a photon gas confined in a vacuum space. Correspondingly, the Debye model treats atomic vibrations as phonons confined in the solid’s volume. Most of the calculation steps are identical, as both are examples of a massless Bose gas with a linear dispersion relation.
For a cube of side-length [math]\displaystyle{ L }[/math], the resonating modes of the sonic disturbances (considering for now only those aligned with one axis), treated as particles in a box, have wavelengths given as
- [math]\displaystyle{ \lambda_n = {2L\over n}\,, }[/math]
where [math]\displaystyle{ n }[/math] is an integer. The energy of a phonon is given as
- [math]\displaystyle{ E_n\ =h\nu_n\,, }[/math]
where [math]\displaystyle{ h }[/math] is the Planck constant and [math]\displaystyle{ \nu_{n} }[/math] is the frequency of the phonon. Making the approximation that the frequency is inversely proportional to the wavelength,
- [math]\displaystyle{ E_n=h\nu_n={hc_{\rm s}\over\lambda_n}={hc_sn\over 2L}\,, }[/math]
in which [math]\displaystyle{ c_s }[/math] is the speed of sound inside the solid. In three dimensions, energy can be generalized to
- [math]\displaystyle{ E_n^2={p_n^2 c_{\rm s}^2}=\left({hc_{\rm s}\over2L}\right)^2\left(n_x^2+n_y^2+n_z^2\right)\,, }[/math]
in which [math]\displaystyle{ p_n }[/math] is the magnitude of the three-dimensional momentum of the phonon, and [math]\displaystyle{ n_x }[/math], [math]\displaystyle{ n_y }[/math], and [math]\displaystyle{ n_z }[/math] are the components of the resonating mode along each of the three axes.
The approximation that the frequency is inversely proportional to the wavelength (giving a constant speed of sound) is good for low-energy phonons but not for high-energy phonons, which is a limitation of the Debye model. This approximation leads to incorrect results at intermediate temperatures, whereas the results are exact at the low and high temperature limits.
The total energy in the box is
- [math]\displaystyle{ E = \sum_n E_n\,\bar{N}(E_n)\,, }[/math]
where [math]\displaystyle{ \bar{N}(E_n) }[/math] is the number of phonons in the box with energy [math]\displaystyle{ E_n }[/math]; the total energy is equal to the sum of energies over all energy level, and the energy at a given level is found by multiplying by the energy level by the number of phonons with that energy. In three dimensions, each combination of modes in each of the three axes corresponds to an energy level, giving the total energy as:
- [math]\displaystyle{ U = \sum_{n_x}\sum_{n_y}\sum_{n_z}E_n\,\bar{N}(E_n)\,. }[/math]
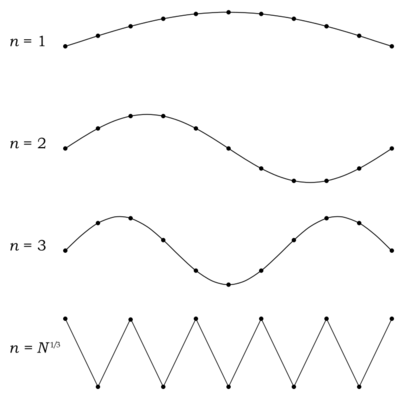
The Debye model and Planck's law of black body radiation differ here with respect to this sum. Unlike electromagnetic photon radiation in a box, there are a finite number of phonon energy states because a phonon cannot have an arbitrarily high frequency. Its frequency is bounded by its propagation medium—the atomic lattice of the solid. The following illustration describes transverse phonons in a cubic solid at varying frequencies:
It is reasonable to assume that the minimum wavelength of a phonon is twice the atomic separation, as shown in the lowest example. With [math]\displaystyle{ N }[/math] atoms in a cubic solid, each axis of the cube measures as being [math]\displaystyle{ \sqrt[3]{N} }[/math] atoms long. Atomic separation is then given by [math]\displaystyle{ L/\sqrt[3]{N} }[/math], and the minimum wavelength is
- [math]\displaystyle{ \lambda_{\rm min} = {2L \over \sqrt[3]{N}}\,, }[/math]
making the maximum mode number [math]\displaystyle{ n_{max} }[/math]:
- [math]\displaystyle{ n_{\rm max} = \sqrt[3]{N}\,. }[/math]
This contrasts with photons, for which the maximum mode number is infinite. This number bounds the upper limit of the triple energy sum
- [math]\displaystyle{ U = \sum_{n_x}^{\sqrt[3]{N}}\sum_{n_y}^{\sqrt[3]{N}}\sum_{n_z}^{\sqrt[3]{N}}E_n\,\bar{N}(E_n)\,. }[/math]
If [math]\displaystyle{ E_n }[/math] is a function that is slowly varying with respect to [math]\displaystyle{ n }[/math], the sums can be approximated with integrals: [math]\displaystyle{ U \approx\int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}} E(n)\,\bar{N}\left(E(n)\right)\,dn_x\, dn_y\, dn_z\,. }[/math]
To evaluate this integral, the function [math]\displaystyle{ \bar{N}(E) }[/math], the number of phonons with energy [math]\displaystyle{ E\,, }[/math] must also be known. Phonons obey Bose–Einstein statistics, and their distribution is given by the Bose–Einstein statistics formula:
- [math]\displaystyle{ \langle N\rangle_{BE} = {1\over e^{E/kT}-1}\,. }[/math]
Because a phonon has three possible polarization states (one longitudinal, and two transverse, which approximately do not affect its energy) the formula above must be multiplied by 3,
- [math]\displaystyle{ \bar{N}(E) = {3\over e^{E/kT}-1}\,. }[/math]
Considering all three polarization states together also means that an effective sonic velocity [math]\displaystyle{ c_{{\rm eff}} }[/math] must be determined and used as the value of the standard sonic velocity [math]\displaystyle{ c_s. }[/math] The Debye temperature [math]\displaystyle{ T_{\rm D} }[/math] defined below is proportional to [math]\displaystyle{ c_{{\rm eff}} }[/math]; more precisely, [math]\displaystyle{ T_{\rm D}^{-3}\propto c_{{\rm eff}}^{-3}:=\frac{1}{3}c_{{\rm long}}^{-3}+\frac{2}{3}c_{{\rm trans}}^{-3} }[/math], where longitudinal and transversal sound-wave velocities are averaged, weighted by the number of polarization states. The Debye temperature or the effective sonic velocity is a measure of the hardness of the crystal.
Substituting [math]\displaystyle{ \bar{N}(E) }[/math] into the energy integral yields
- [math]\displaystyle{ U = \int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}}\int_0^{\sqrt[3]{N}} E(n)\,{3\over e^{E(n)/kT}-1}\,dn_x\, dn_y\, dn_z\,. }[/math]
These integrals are evaluated for photons easily because their frequency, at least semi-classically, is unbound. The same is not true for phonons, so in order to approximate this triple integral, Peter Debye used spherical coordinates,
- [math]\displaystyle{ \ (n_x,n_y,n_z)=(n\sin \theta \cos \phi,n\sin \theta \sin \phi,n\cos \theta )\,, }[/math]
and approximated the cube with an eighth of a sphere,
- [math]\displaystyle{ U \approx\int_0^{\pi/2}\int_0^{\pi/2}\int_0^R E(n)\,{3\over e^{E(n)/kT}-1}n^2 \sin\theta\, dn\, d\theta\, d\phi\,, }[/math]
where [math]\displaystyle{ R }[/math] is the radius of this sphere. As the energy function does not depend on either of the angles, the equation can be simplified to
- [math]\displaystyle{ \,3 \int_0^{\pi/2}\int_0^{\pi/2}\sin\theta\, d\theta\, d\phi\,\int_0^R E(n)\,\frac{1}{e^{E(n)/kT}-1}n^2 dn\, = \frac{3\pi}{2} \int_0^R E(n)\,\frac{1}{e^{E(n)/kT}-1}n^2 dn\, }[/math]
The number of particles in the original cube and in the eighth of a sphere should be equivalent. The volume of the cube is [math]\displaystyle{ N }[/math] unit cell volumes,
- [math]\displaystyle{ N = {1\over8}{4\over3}\pi R^3\,, }[/math]
such that the radius must be
- [math]\displaystyle{ R = \sqrt[3]{6N\over\pi}\,. }[/math]
The substitution of integration over a sphere for the correct integral over a cube introduces another source of inaccuracy into the resulting model.
After making the spherical substitution and substituting in the function [math]\displaystyle{ E(n)\, }[/math], the energy integral becomes
- [math]\displaystyle{ U = {3\pi\over2}\int_0^R \,{hc_sn\over 2L}{n^2\over e^{hc_{\rm s}n/2LkT}-1} \,dn }[/math].
Changing the integration variable to [math]\displaystyle{ x = {hc_{\rm s}n\over 2LkT} }[/math],
- [math]\displaystyle{ U = {3\pi\over2} kT \left({2LkT\over hc_{\rm s}}\right)^3\int_0^{hc_{\rm s}R/2LkT} {x^3\over e^x-1}\, dx. }[/math]
To simplify the appearance of this expression, define the Debye temperature [math]\displaystyle{ T_{\rm D} }[/math]
- [math]\displaystyle{ T_{\rm D}\ \stackrel{\mathrm{def}}{=}\ {hc_{\rm s}R\over2Lk} = {hc_{\rm s}\over2Lk}\sqrt[3]{6N\over\pi} = {hc_{\rm s} \over 2k} \sqrt[3]{{6\over\pi}{N\over V}} }[/math]
where [math]\displaystyle{ V }[/math] is the volume of the cubic box of side-length [math]\displaystyle{ L }[/math].
Some authors[2][3] describe the Debye temperature as shorthand for some constants and material-dependent variables. However, [math]\displaystyle{ kT_{\rm D} }[/math] is roughly equal to the phonon energy of the minimum wavelength mode, and so we can interpret the Debye temperature as the temperature at which the highest-frequency mode is excited. Additionally, since all other modes are of a lower energy than the highest-frequency mode, all modes are excited at this temperature.[original research?]
From the total energy, the specific internal energy can be calculated:
- [math]\displaystyle{ \frac{U}{Nk} = 9T \left({T\over T_{\rm D}}\right)^3\int_0^{T_{\rm D}/T} {x^3\over e^x-1}\, dx = 3T D_3 \left({T_{\rm D}\over T}\right)\,, }[/math]
where [math]\displaystyle{ D_3(x) }[/math] is the third Debye function. Differentiating this function with respect to [math]\displaystyle{ T }[/math] produces the dimensionless heat capacity:
- [math]\displaystyle{ \frac{C_V}{Nk} = 9 \left({T\over T_{\rm D}}\right)^3\int_0^{T_{\rm D}/T} {x^4 e^x\over\left(e^x-1\right)^2}\, dx\,. }[/math]
These formulae treat the Debye model at all temperatures. The more elementary formulae given further down give the asymptotic behavior in the limit of low and high temperatures. The essential reason for the exactness at low and high energies is, respectively, that the Debye model gives the exact dispersion relation [math]\displaystyle{ E(\nu ) }[/math] at low frequencies, and corresponds to the exact density of states [math]\displaystyle{ (\int g(\nu ) \, d\nu\equiv 3N) }[/math] at high temperatures, concerning the number of vibrations per frequency interval.[original research?]
Debye's derivation
Debye derived his equation differently and more simply. Using continuum mechanics, he found that the number of vibrational states with a frequency less than a particular value was asymptotic to
- [math]\displaystyle{ n \sim {1 \over 3} \nu^3 V F\,, }[/math]
in which [math]\displaystyle{ V }[/math] is the volume and [math]\displaystyle{ F }[/math] is a factor that he calculated from elasticity coefficients and density. Combining this formula with the expected energy of a harmonic oscillator at temperature [math]\displaystyle{ T }[/math] (already used by Einstein in his model) would give an energy of
- [math]\displaystyle{ U = \int_0^\infty \,{h\nu^3 V F\over e^{h\nu/kT}-1}\, d\nu\,, }[/math]
if the vibrational frequencies continued to infinity. This form gives the [math]\displaystyle{ T^3 }[/math] behaviour which is correct at low temperatures. But Debye realized that there could not be more than [math]\displaystyle{ 3N }[/math] vibrational states for N atoms. He made the assumption that in an atomic solid, the spectrum of frequencies of the vibrational states would continue to follow the above rule, up to a maximum frequency [math]\displaystyle{ \nu_m }[/math]chosen so that the total number of states is
- [math]\displaystyle{ 3N = {1 \over 3} \nu_m^3 V F \,. }[/math]
Debye knew that this assumption was not really correct (the higher frequencies are more closely spaced than assumed), but it guarantees the proper behaviour at high temperature (the Dulong–Petit law). The energy is then given by
- [math]\displaystyle{ \begin{align} U &= \int_0^{\nu_m} \,{h\nu^3 V F\over e^{h\nu/kT}-1}\, d\nu\,,\\ &= V F kT (kT/h)^3 \int_0^{T_{\rm D}/T} \,{x^3 \over e^x-1}\, dx\,. \end{align} }[/math]
Substituting [math]\displaystyle{ T_{\rm D} }[/math] for [math]\displaystyle{ h\nu_m/k }[/math],
- [math]\displaystyle{ \begin{align} U &= 9 N k T (T/T_{\rm D})^3 \int_0^{T_{\rm D}/T} \,{x^3 \over e^x-1}\, dx\,, \\ &= 3 N k T D_3(T_{\rm D}/T)\,, \end{align} }[/math]
where [math]\displaystyle{ D_3 }[/math] is the function later given the name of third-order Debye function.
Another derivation
First the vibrational frequency distribution is derived from Appendix VI of Terrell L. Hill's An Introduction to Statistical Mechanics.[4] Consider a three-dimensional isotropic elastic solid with N atoms in the shape of a rectangular parallelepiped with side-lengths [math]\displaystyle{ L_x, L_y, L_z }[/math]. The elastic wave will obey the wave equation and will be plane waves; consider the wave vector [math]\displaystyle{ \mathbf{k} = (k_x, k_y, k_z) }[/math] and define [math]\displaystyle{ l_x=\frac{k_x}{|\mathbf{k}|}, l_y=\frac{k_y}{|\mathbf{k}|}, l_z=\frac{k_z}{|\mathbf{k}|} }[/math], such that
-
[math]\displaystyle{ l_x^2 + l_y^2 + l_z^2 = 1. }[/math]
()
Solutions to the wave equation are
- [math]\displaystyle{ u(x,y,z,t) = \sin(2\pi\nu t)\sin\left(\frac{2\pi l_x x}{\lambda}\right)\sin\left(\frac{2\pi l_y y}{\lambda}\right)\sin\left(\frac{2\pi l_z z}{\lambda}\right) }[/math]
and with the boundary conditions [math]\displaystyle{ u=0 }[/math] at [math]\displaystyle{ x,y,z=0, x=L_x, y=L_y, z=L_z }[/math],
-
[math]\displaystyle{ \frac{2l_xL_x}{\lambda}=n_x; \frac{2l_yL_y}{\lambda}=n_y; \frac{2l_zL_z}{\lambda}=n_z }[/math]
()
where [math]\displaystyle{ n_x,n_y,n_z }[/math] are positive integers. Substituting (2) into (1) and also using the dispersion relation [math]\displaystyle{ c_s=\lambda\nu }[/math],
- [math]\displaystyle{ \frac{n_x^2}{(2\nu L_x/c_s)^2} + \frac{n_y^2}{(2\nu L_y/c_s)^2} + \frac{n_z^2}{(2\nu L_z/c_s)^2} = 1. }[/math]
The above equation, for fixed frequency [math]\displaystyle{ \nu }[/math], describes an eighth of an ellipse in "mode space" (an eighth because [math]\displaystyle{ n_x,n_y,n_z }[/math] are positive). The number of modes with frequency less than [math]\displaystyle{ \nu }[/math] is thus the number of integral points inside the ellipse, which, in the limit of [math]\displaystyle{ L_x,L_y,L_z \to\infty }[/math] (i.e. for a very large parallelepiped) can be approximated to the volume of the ellipse. Hence, the number of modes [math]\displaystyle{ N(\nu) }[/math] with frequency in the range [math]\displaystyle{ [0,\nu] }[/math] is
-
[math]\displaystyle{ N(\nu) = \frac{1}{8}\frac{4\pi}{3}\left(\frac{2\nu}{c_{\mathrm{s}}}\right)^3L_xL_yL_z = \frac{4\pi\nu^3V}{3c_{\mathrm{s}}^3}, }[/math]
()
where [math]\displaystyle{ V=L_xL_yL_z }[/math] is the volume of the parallelepiped. The wave speed in the longitudinal direction is different from the transverse direction and that the waves can be polarised one way in the longitudinal direction and two ways in the transverse direction and ca be defined as [math]\displaystyle{ \frac{3}{c_s^3} = \frac{1}{c_\text{long}^3} + \frac{2}{c_\text{trans}^3} }[/math].
Following the derivation from A First Course in Thermodynamics,[5] an upper limit to the frequency of vibration is defined [math]\displaystyle{ \nu_D }[/math]; since there are [math]\displaystyle{ N }[/math] atoms in the solid, there are [math]\displaystyle{ 3N }[/math] quantum harmonic oscillators (3 for each x-, y-, z- direction) oscillating over the range of frequencies [math]\displaystyle{ [0,\nu_D] }[/math]. [math]\displaystyle{ \nu_D }[/math] can be determined using
-
[math]\displaystyle{ 3N = N(\nu_{\rm D}) = \frac{4\pi\nu_{\rm D}^3V}{3c_{\rm s}^3} }[/math].
()
By defining [math]\displaystyle{ \nu_{\rm D} = \frac{kT_{\rm D}}{h} }[/math], where k is the Boltzmann constant and h is the Planck constant, and substituting (4) into (3),
-
[math]\displaystyle{ N(\nu) = \frac{3Nh^3\nu^3}{k^3T_{\rm D}^3}, }[/math]
()
this definition is more standard; the energy contribution for all oscillators oscillating at frequency [math]\displaystyle{ \nu }[/math] can be found. Quantum harmonic oscillators can have energies [math]\displaystyle{ E_i = (i+1/2)h\nu }[/math] where [math]\displaystyle{ i = 0,1,2,\dotsc }[/math] and using Maxwell-Boltzmann statistics, the number of particles with energy [math]\displaystyle{ E_i }[/math] is
- [math]\displaystyle{ n_i=\frac{1}{A}e^{-E_i/(kT)}=\frac{1}{A}e^{-(i+1/2)h\nu/(kT)}. }[/math]
The energy contribution for oscillators with frequency [math]\displaystyle{ \nu }[/math] is then
-
[math]\displaystyle{ dU(\nu) = \sum_{i=0}^\infty E_i\frac{1}{A}e^{-E_i/(kT)} }[/math].
()
By noting that [math]\displaystyle{ \sum_{i=0}^\infty n_i = dN(\nu) }[/math] (because there are [math]\displaystyle{ dN(\nu) }[/math] modes oscillating with frequency [math]\displaystyle{ \nu }[/math]),
- [math]\displaystyle{ \frac{1}{A}e^{-1/2h\nu/(kT)}\sum_{i=0}^\infty e^{-ih\nu/(kT)} = \frac{1}{A}e^{-1/2h\nu/(kT)}\frac{1}{1-e^{-h\nu/(kT)}} = dN(\nu) . }[/math]
From above, we can get an expression for 1/A; substituting it into (6),
- [math]\displaystyle{ \begin{align} dU &= dN(\nu)e^{1/2h\nu/(kT)}(1-e^{-h\nu/(kT)})\sum_{i=0}^\infty h\nu(i+1/2)e^{-h\nu(i+1/2)/(kT)} \\ \\ &=dN(\nu)(1-e^{-h\nu/(kT)})\sum_{i=0}^\infty h\nu(i+1/2)e^{-h\nu i/(kT)} \\ &=dN(\nu)h\nu\left(\frac{1}{2}+(1-e^{-h\nu/(kT)})\sum_{i=0}^\infty ie^{-h\nu i/(kT)}\right) \\ &=dN(\nu)h\nu\left(\frac{1}{2}+\frac{1}{e^{h\nu/(kT)}-1}\right). \end{align} }[/math]
Integrating with respect to ν yields
- [math]\displaystyle{ U = \frac{9Nh^4}{k^3T_{\rm D}^3}\int_0^{\nu_D}\left(\frac{1}{2}+\frac{1}{e^{h\nu/(kT)}-1}\right)\nu^3 d\nu. }[/math]
Temperature limits
The temperature of a Debye solid is said to be low if [math]\displaystyle{ T \ll T_{\rm D} }[/math], leading to
- [math]\displaystyle{ \frac{C_V}{Nk} \sim 9 \left({T\over T_{\rm D}}\right)^3\int_0^{\infty} {x^4 e^x\over \left(e^x-1\right)^2}\, dx. }[/math]
This definite integral can be evaluated exactly:
- [math]\displaystyle{ \frac{C_V}{Nk} \sim {12\pi^4\over5} \left({T\over T_{\rm D}}\right)^3. }[/math]
In the low-temperature limit, the limitations of the Debye model mentioned above do not apply, and it gives a correct relationship between (phononic) heat capacity, temperature, the elastic coefficients, and the volume per atom (the latter quantities being contained in the Debye temperature).
The temperature of a Debye solid is said to be high if [math]\displaystyle{ T \gg T_{\rm D} }[/math]. Using [math]\displaystyle{ e^x - 1\approx x }[/math] if [math]\displaystyle{ |x| \ll 1 }[/math] leads to
- [math]\displaystyle{ \frac{C_V}{Nk} \sim 9 \left({T\over T_{\rm D}}\right)^3\int_0^{T_{\rm D}/T} {x^4 \over x^2}\, dx }[/math]
which upon integration gives
- [math]\displaystyle{ \frac{C_V}{Nk} \sim 3\,. }[/math]
This is the Dulong–Petit law, and is fairly accurate although it does not take into account anharmonicity, which causes the heat capacity to rise further. The total heat capacity of the solid, if it is a conductor or semiconductor, may also contain a non-negligible contribution from the electrons.
Debye versus Einstein
The Debye and Einstein models correspond closely to experimental data, but the Debye model is correct at low temperatures whereas the Einstein model is not. To visualize the difference between the models, one would naturally plot the two on the same set of axes, but this is not immediately possible as both the Einstein model and the Debye model provide a functional form for the heat capacity. As models, they require scales to relate them to their real-world counterparts. One can see that the scale of the Einstein model is given by [math]\displaystyle{ \epsilon/k }[/math]:
- [math]\displaystyle{ C_V = 3Nk\left({\epsilon\over k T}\right)^2{e^{\epsilon/kT}\over \left(e^{\epsilon/kT}-1\right)^2}. }[/math]
The scale of the Debye model is [math]\displaystyle{ T_{\rm D} }[/math], the Debye temperature. Both are usually found by fitting the models to the experimental data. (The Debye temperature can theoretically be calculated from the speed of sound and crystal dimensions.) Because the two methods approach the problem from different directions and different geometries, Einstein and Debye scales are not the same, that is to say
- [math]\displaystyle{ {\epsilon\over k} \ne T_{\rm D}\,, }[/math]
which means that plotting them on the same set of axes makes no sense. They are two models of the same thing, but of different scales. If one defines the Einstein condensation temperature as
- [math]\displaystyle{ T_{\rm E} \ \stackrel{\mathrm{def}}{=}\ {\epsilon\over k}\,, }[/math]
then one can say
- [math]\displaystyle{ T_{\rm E} \ne T_{\rm D}\,, }[/math]
and, to relate the two, the ratio[math]\displaystyle{ \frac{T_{\rm E}}{ T_{\rm D}} \, }[/math] is used.
The Einstein solid is composed of single-frequency quantum harmonic oscillators, [math]\displaystyle{ \epsilon = \hbar\omega = h\nu }[/math]. That frequency, if it indeed existed, would be related to the speed of sound in the solid. If one imagines the propagation of sound as a sequence of atoms hitting one another, then the frequency of oscillation must correspond to the minimum wavelength sustainable by the atomic lattice, [math]\displaystyle{ \lambda_{min} }[/math], where
- [math]\displaystyle{ \nu = {c_{\rm s}\over\lambda} = {c_{\rm s}\sqrt[3]{N}\over 2L} = {c_{\rm s}\over 2}\sqrt[3]{N\over V} }[/math],
which makes the Einstein temperature [math]\displaystyle{ T_{\rm E} = {\epsilon\over k} = {h\nu\over k} = {h c_{\rm s}\over 2k}\sqrt[3]{N\over V}\,, }[/math] and the sought ratio is therefore
- [math]\displaystyle{ {T_{\rm E}\over T_{\rm D}} = \sqrt[3]{\pi\over6}\ = 0.805995977... }[/math]
Using the ratio, both models can be plotted on the same graph. It is the cube root of the ratio of the volume of one octant of a three-dimensional sphere to the volume of the cube that contains it, which is just the correction factor used by Debye when approximating the energy integral above. Alternatively, the ratio of the two temperatures can be seen to be the ratio of Einstein's single frequency at which all oscillators oscillate and Debye's maximum frequency. Einstein's single frequency can then be seen to be a mean of the frequencies available to the Debye model.
Debye temperature table
Even though the Debye model is not completely correct, it gives a good approximation for the low temperature heat capacity of insulating, crystalline solids where other contributions (such as highly mobile conduction electrons) are negligible. For metals, the electron contribution to the heat is proportional to [math]\displaystyle{ T }[/math], which at low temperatures dominates the Debye [math]\displaystyle{ T^3 }[/math] result for lattice vibrations. In this case, the Debye model can only be said to approximate the lattice contribution to the specific heat. The following table lists Debye temperatures for several pure elements[2] and sapphire:
|
|
|
|
The Debye model's fit to experimental data is often phenomenologically improved by allowing the Debye temperature to become temperature dependent;[6] for example, the value for ice increases from about 222 K[7] to 300 K[8] as the temperature goes from absolute zero to about 100 K.
Extension to other quasi-particles
For other bosonic quasi-particles, e.g., magnons (quantized spin waves) in ferromagnets instead of the phonons (quantized sound waves), one can derive analogous results. In this case at low frequencies one has different dispersion relations of momentum and energy, e.g., [math]\displaystyle{ E(\nu )\propto k^2 }[/math] in the case of magnons, instead of [math]\displaystyle{ E(\nu )\propto k }[/math] for phonons (with [math]\displaystyle{ k=2\pi /\lambda }[/math]). One also has different density of states (e.g., [math]\displaystyle{ \int g(\nu ){\rm d}\nu \equiv N\, }[/math]). As a consequence, in ferromagnets one gets a magnon contribution to the heat capacity, [math]\displaystyle{ \Delta C_{\,{\rm V|\,magnon}}\,\propto T^{3/2} }[/math], which dominates at sufficiently low temperatures the phonon contribution, [math]\displaystyle{ \,\Delta C_{\,{\rm V|\,phonon}}\propto T^3 }[/math]. In metals, in contrast, the main low-temperature contribution to the heat capacity, [math]\displaystyle{ \propto T }[/math], comes from the electrons. It is fermionic, and is calculated by different methods going back to Sommerfeld's free electron model.[citation needed]
Extension to liquids
It was long thought that phonon theory is not able to explain the heat capacity of liquids, since liquids only sustain longitudinal, but not transverse phonons, which in solids are responsible for 2/3 of the heat capacity. However, Brillouin scattering experiments with neutrons and with X-rays, confirming an intuition of Yakov Frenkel,[9] have shown that transverse phonons do exist in liquids, albeit restricted to frequencies above a threshold called the Frenkel frequency. Since most energy is contained in these high-frequency modes, a simple modification of the Debye model is sufficient to yield a good approximation to experimental heat capacities of simple liquids.[10] More recently, it has been shown that instantaneous normal modes associated with relaxations from saddle points in the liquid energy landscape, which dominate the frequency spectrum of liquids at low frequencies, may determine the specific heat of liquids as a function of temperature over a broad range.[11]
Debye frequency
The Debye frequency (Symbol: [math]\displaystyle{ \omega_{\rm Debye} }[/math] or [math]\displaystyle{ \omega_{\rm D} }[/math]) is a parameter in the Debye model that refers to a cut-off angular frequency for waves of a harmonic chain of masses, used to describe the movement of ions in a crystal lattice and more specifically, to correctly predict that the heat capacity in such crystals is constant at high temperatures (Dulong–Petit law). The concept was first introduced by Peter Debye in 1912.[12]
Throughout this section, periodic boundary conditions are assumed.
Definition
Assuming the dispersion relation is
- [math]\displaystyle{ \omega = v_{\rm s} |\mathbf k| , }[/math]
with [math]\displaystyle{ v_{\rm s} }[/math] the speed of sound in the crystal and k the wave vector, the value of the Debye frequency is as follows:
For a one-dimensional monatomic chain, the Debye frequency is equal to[13]
- [math]\displaystyle{ \omega_{\rm D} = v_{\rm s} \pi / a = v_{\rm s} \pi N / L = v_{\rm s} \pi \lambda , }[/math]
with [math]\displaystyle{ a }[/math] as the distance between two neighbouring atoms in the chain when the system is in its ground state of energy, here being that none of the atoms are moving with respect to one another; [math]\displaystyle{ N }[/math] the total number of atoms in the chain; [math]\displaystyle{ L }[/math] the size of the system, which is the length of the chain; and [math]\displaystyle{ \lambda }[/math] the linear number density. For [math]\displaystyle{ L }[/math], [math]\displaystyle{ N }[/math], and [math]\displaystyle{ a }[/math], the relation [math]\displaystyle{ L = N a }[/math] holds.
For a two-dimensional monatomic square lattice, the Debye frequency is equal to
- [math]\displaystyle{ \omega_{\rm D}^2 = \frac {4 \pi}{a^2} v_{\rm s}^2 = \frac {4 \pi N}{A} v_{\rm s}^2 \equiv 4 \pi \sigma v_{\rm s}^2 , }[/math]
with [math]\displaystyle{ A \equiv L^{2} = N a^{2} }[/math] is the size (area) of the surface, and [math]\displaystyle{ \sigma }[/math] the surface number density.
For a three-dimensional monatomic primitive cubic crystal, the Debye frequency is equal to[14]
- [math]\displaystyle{ \omega_{\rm D}^3 = \frac {6 \pi^2}{a^3} v_{\rm s}^3 = \frac {6 \pi^2 N}{V} v_{\rm s}^3 \equiv 6 \pi^2 \rho v_{\rm s}^3 , }[/math]
with [math]\displaystyle{ V \equiv L^3 = N a^3 }[/math] the size of the system, and [math]\displaystyle{ \rho }[/math] the volume number density.
The general formula for the Debye frequency as a function of [math]\displaystyle{ n }[/math], the number of dimensions for a (hyper)cubic lattice is
- [math]\displaystyle{ \omega_{\rm D}^n = 2^n \pi^{n/2} \Gamma\left(1+\tfrac{n}{2}\right) \frac {N}{L^n} v_{\rm s}^n , }[/math]
with [math]\displaystyle{ \Gamma }[/math] being the gamma function.
The speed of sound in the crystal depends on the mass of the atoms, the strength of their interaction, the pressure on the system, and the polarisation of the spin wave (longitudinal or transverse), among others. For the following, the speed of sound is assumed to be the same for any polarisation, although this limits the applicability of the result.[15]
The assumed dispersion relation is easily proven inaccurate for a one-dimensional chain of masses, but in Debye's model, this does not prove to be problematic.[citation needed]
Relation to Debye's temperature
The Debye temperature [math]\displaystyle{ \theta_{\rm D} }[/math], another parameter in Debye model, is related to the Debye frequency by the relation [math]\displaystyle{ \theta_{\rm D}=\frac{\hbar}{k_{\rm B}}\omega_{\rm D}, }[/math] where [math]\displaystyle{ \hbar }[/math] is the reduced Planck constant and [math]\displaystyle{ k_{\rm B} }[/math]is the Boltzmann constant.
Debye's derivation
Three-dimensional crystal
In Debye's derivation of the heat capacity, he sums over all possible modes of the system, accounting for different directions and polarisations. He assumed the total number of modes per polarization to be [math]\displaystyle{ N }[/math], the amount of masses in the system, and the total to be[15]
- [math]\displaystyle{ \sum_{\rm modes}3=3 N, }[/math]
with three polarizations per mode. The sum runs over all modes without differentiating between different polarizations, and then counts the total number of polarization-mode combinations. Debye made this assumption based on an assumption from classical mechanics that the number of modes per polarization in a chain of masses should always be equal to the number of masses in the chain.
The left hand side can be made explicit to show how it depends on the Debye frequency, introduced first as a cut-off frequency beyond which no frequencies exist. By relating the cut-off frequency to the maximum number of modes, an expression for the cut-off frequency can be derived.
First of all, by assuming [math]\displaystyle{ L }[/math] to be very large ([math]\displaystyle{ L }[/math] ≫ 1, with [math]\displaystyle{ L }[/math] the size of the system in any of the three directions) the smallest wave vector in any direction could be approximated by: [math]\displaystyle{ d k_i = 2 \pi / L }[/math], with [math]\displaystyle{ i = x, y, z }[/math]. Smaller wave vectors cannot exist because of the periodic boundary conditions. Thus the summation would become[16]
- [math]\displaystyle{ \sum_{\rm modes}3=\frac {3 V}{(2 \pi)^3} \iiint d \mathbf k, }[/math]
where [math]\displaystyle{ \mathbf k \equiv (k_x, k_y, k_z) }[/math]; [math]\displaystyle{ V \equiv L^3 }[/math] is the size of the system; and the integral is (as the summation) over all possible modes, which is assumed to be a finite region (bounded by the cut-off frequency).
The triple integral could be rewritten as a single integral over all possible values of the absolute value of [math]\displaystyle{ \mathbf k }[/math] (see Jacobian for spherical coordinates). The result is
- [math]\displaystyle{ \frac {3 V}{(2 \pi)^3} \iiint d \mathbf k = \frac {3 V}{2 \pi^2} \int_0^{k_{\rm D}} |\mathbf k|^2 d \mathbf k , }[/math]
with [math]\displaystyle{ k_{\rm D} }[/math] the absolute value of the wave vector corresponding with the Debye frequency, so [math]\displaystyle{ k_{\rm D} = \omega_{\rm D}/v_{\rm s} }[/math].
Since the dispersion relation is [math]\displaystyle{ \omega =v_{\rm s}|\mathbf k| }[/math], it can be written as an integral over all possible [math]\displaystyle{ \omega }[/math]:
- [math]\displaystyle{ \frac {3 V}{2 \pi^2} \int_0^{k_{\rm D}} |\mathbf k|^2 d \mathbf k = \frac {3 V}{2 \pi^2 v_{\rm s}^3} \int_0^{\omega_{\rm D}} \omega^2 d \omega , }[/math]
After solving the integral it is again equated to [math]\displaystyle{ 3 N }[/math] to find
- [math]\displaystyle{ \frac {V}{2 \pi^2 v_{\rm s}^3} \omega_{\rm D}^3 = 3 N . }[/math]
It can be rearranged into
- [math]\displaystyle{ \omega_{\rm D}^3 =\frac {6 \pi^2 N}{V} v_{\rm s}^3 . }[/math]
One-dimensional chain in 3D space
The same derivation could be done for a one-dimensional chain of atoms. The number of modes remains unchanged, because there are still three polarizations, so
- [math]\displaystyle{ \sum_{\rm modes}3=3 N. }[/math]
The rest of the derivation is analogous to the previous, so the left hand side is rewritten with respect to the Debye frequency:
- [math]\displaystyle{ \sum_{\rm modes}3=\frac {3 L}{2 \pi} \int_{-k_{\rm D}}^{k_{\rm D}}d k = \frac {3 L}{\pi v_{\rm s}} \int_{0}^{\omega_{\rm D}}d \omega. }[/math]
The last step is multiplied by two is because the integrand in the first integral is even and the bounds of integration are symmetric about the origin, so the integral can be rewritten as from 0 to [math]\displaystyle{ k_D }[/math] after scaling by a factor of 2. This is also equivalent to the statement that the volume of a one-dimensional ball is twice its radius. Applying a change a substitution of [math]\displaystyle{ k=\frac{\omega}{v_s} }[/math] , our bounds are now 0 to [math]\displaystyle{ \omega_D = k_Dv_s }[/math], which gives us our rightmost integral. We continue;
- [math]\displaystyle{ \frac {3 L}{\pi v_{\rm s}} \int_{0}^{\omega_{\rm D}}d \omega = \frac {3 L}{\pi v_{\rm s}} \omega_{\rm D} = 3 N . }[/math]
Conclusion:
- [math]\displaystyle{ \omega_{\rm D} = \frac {\pi v_{\rm s} N}{L} . }[/math]
Two-dimensional crystal
The same derivation could be done for a two-dimensional crystal. The number of modes remains unchanged, because there are still three polarizations. The derivation is analogous to the previous two. We start with the same equation,
- [math]\displaystyle{ \sum_{\rm modes}3=3 N. }[/math]
And then the left hand side is rewritten and equated to [math]\displaystyle{ 3N }[/math]
- [math]\displaystyle{ \sum_{\rm modes}3=\frac {3 A}{(2 \pi)^2} \iint d \mathbf k = \frac {3 A}{2 \pi v_{\rm s}^2} \int_{0}^{\omega_{\rm D}} \omega d \omega = \frac {3 A \omega_{\rm D}^2}{4 \pi v_{\rm s}^2} = 3 N , }[/math]
where [math]\displaystyle{ A \equiv L^2 }[/math] is the size of the system.
It can be rewritten as
- [math]\displaystyle{ \omega_{\rm D}^2 = \frac {4 \pi N}{A} v_{\rm s}^2 . }[/math]
Polarization dependence
In reality, longitudinal waves often have a different wave velocity from that of transverse waves. Making the assumption that the velocities are equal simplified the final result, but reintroducing the distinction improves the accuracy of the final result.
The dispersion relation becomes [math]\displaystyle{ \omega_i = v_{s,i}|\mathbf k| }[/math], with [math]\displaystyle{ i = 1, 2, 3 }[/math], each corresponding to one of the three polarizations. The cut-off frequency [math]\displaystyle{ \omega_{\rm D} }[/math], however, does not depend on [math]\displaystyle{ i }[/math]. We can write the total number of modes as [math]\displaystyle{ \sum_{i}\sum_{\rm modes} 1 }[/math], which is again equal to [math]\displaystyle{ 3 N }[/math]. Here the summation over the modes is now dependent on [math]\displaystyle{ i }[/math].
One-dimensional chain in 3D space
The summation over the modes is rewritten
- [math]\displaystyle{ \sum_{i}\sum_{\rm modes} 1 = \sum_i \frac {L}{\pi v_{s,i}} \int_0^{\omega_{\rm D}} d \omega_i = 3 N . }[/math]
The result is
- [math]\displaystyle{ \frac {L \omega_{\rm D}}{\pi} (\frac {1}{v_{s,1}} + \frac {1}{v_{s,2}} + \frac {1}{v_{s,3}}) = 3 N . }[/math]
Thus the Debye frequency is found
- [math]\displaystyle{ \omega_{\rm D} = \frac{ \pi N}{L} \frac{3}{\frac {1}{v_{s,1}} + \frac {1}{v_{s,2}} + \frac {1}{v_{s,3}}} = \frac {3 \pi N}{L} \frac {v_{s,1} v_{s,2} v_{s,3}}{v_{s,2} v_{s,3} + v_{s,1} v_{s,3} + v_{s,1} v_{s,2}} = \frac{\pi N}{L} v_{\mathrm{eff}}\,. }[/math]
The calculated effective velocity [math]\displaystyle{ v_{\mathrm{eff}} }[/math] is the harmonic mean of the velocities for each polarization. By assuming the two transverse polarizations to have the same phase speed and frequency,
- [math]\displaystyle{ \omega_{\rm D} = \frac {3 \pi N}{L} \frac {v_{s,t}v_{s,l}}{2v_{s,l} + v_{s,t}} . }[/math]
Setting [math]\displaystyle{ v_{s,t} = v_{s,l} }[/math] recovers the expression previously derived under the assumption that velocity is the same for all polarization modes.
Two-dimensional crystal
The same derivation can be done for a two-dimensional crystal to find
- [math]\displaystyle{ \omega_{\rm D}^2 = \frac {4 \pi N}{A} \frac{3}{\frac {1}{v_{s,1}^2} + \frac {1}{v_{s,2}^2} + \frac {1}{v_{s,3}^2}} = \frac {12 \pi N}{A} \frac {(v_{s,1} v_{s,2} v_{s,3})^2}{(v_{s,2} v_{s,3})^2 + (v_{s,1} v_{s,3})^2 + (v_{s,1} v_{s,2})^2} = \frac{4 \pi N}{A} v_{\mathrm{eff}}^2\,. }[/math]
The calculated effective velocity [math]\displaystyle{ v_{\mathrm{eff}} }[/math] is the square root of the harmonic mean of the squares of velocities. By assuming the two transverse polarizations to be the same,
- [math]\displaystyle{ \omega_{\rm D}^2 = \frac {12 \pi N}{A} \frac {(v_{s,t} v_{s,l})^2}{2 v_{s,l}^2 + v_{s,t}^2} . }[/math]
Setting [math]\displaystyle{ v_{s,t} = v_{s,l} }[/math] recovers the expression previously derived under the assumption that velocity is the same for all polarization modes.
Three-dimensional crystal
The same derivation can be done for a three-dimensional crystal to find (the derivation is analogous to previous derivations)
- [math]\displaystyle{ \omega_{\rm D}^2 = \frac{6 \pi^2 N}{V} \frac{3}{\frac {1}{v_{s,1}^3} + \frac {1}{v_{s,2}^3} + \frac {1}{v_{s,3}^3}} = \frac {18 \pi^2 N}{V} \frac {(v_{s,1} v_{s,2} v_{s,3})^3}{(v_{s,2} v_{s,3})^3 + (v_{s,1} v_{s,3})^3 + (v_{s,1} v_{s,2})^3 } = \frac{6 \pi^2 N}{V} v_{\mathrm{eff}}^3\,. }[/math]
The calculated effective velocity [math]\displaystyle{ v_{\mathrm{eff}} }[/math] is the cube root of the harmonic mean of the cubes of velocities. By assuming the two transverse polarizations to be the same,
- [math]\displaystyle{ \omega_{\rm D}^3 = \frac {18 \pi^2 N}{V} \frac {(v_{s,t} v_{s,l})^3}{2 v_{s,l}^3 + v_{s,t}^3} . }[/math]
Setting [math]\displaystyle{ v_{s,t} = v_{s,l} }[/math] recovers the expression previously derived under the assumption that velocity is the same for all polarization modes.
Derivation with the actual dispersion relation

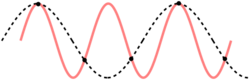
This problem could be made more applicable by relaxing the assumption of linearity of the dispersion relation. Instead of using the dispersion relation [math]\displaystyle{ \omega = v_{\rm s} k }[/math], a more accurate dispersion relation can be used. In classical mechanics, it is known that for an equidistant chain of masses which interact harmonically with each other, the dispersion relation is[15]
[math]\displaystyle{ \omega (k) = 2 \sqrt {\frac {\kappa}{m}}\left|\sin\left(\frac {k a}{2}\right)\right| , }[/math]
with [math]\displaystyle{ m }[/math] being the mass of each atom, [math]\displaystyle{ \kappa }[/math] the spring constant for the harmonic oscillator, and [math]\displaystyle{ a }[/math] still being the spacing between atoms in the ground state. After plotting this relation, Debye's estimation of the cut-off wavelength based on the linear assumption remains accurate, because for every wavenumber bigger than [math]\displaystyle{ \pi / a }[/math] (that is, for [math]\displaystyle{ \lambda }[/math] is smaller than [math]\displaystyle{ 2 a }[/math]), a wavenumber that is smaller than [math]\displaystyle{ \pi / a }[/math] could be found with the same angular frequency. This means the resulting physical manifestation for the mode with the larger wavenumber is indistinguishable from the one with the smaller wavenumber. Therefore, the study of the dispersion relation can be limited to the first Brillouin zone [math]\displaystyle{ k \in \left[-\frac{\pi}{a},\frac{\pi}{a}\right] }[/math] without any loss of accuracy or information.[17] This is possible because the system consists of discretized points, as is demonstrated in the animated picture. Dividing the dispersion relation by [math]\displaystyle{ k }[/math] and inserting [math]\displaystyle{ \pi / a }[/math] for [math]\displaystyle{ k }[/math], we find the speed of a wave with [math]\displaystyle{ k = \pi / a }[/math] to be [math]\displaystyle{ v_{\rm s}(k = \pi / a) = \frac {2 a}{\pi} \sqrt {\frac {\kappa}{m}} . }[/math]
By simply inserting [math]\displaystyle{ k = \pi/a }[/math] in the original dispersion relation we find [math]\displaystyle{ \omega(k = \pi / a) = 2 \sqrt {\frac {\kappa}{m}} = \omega_{\rm D} . }[/math]
Combining these results the same result is once again found [math]\displaystyle{ \omega_{\rm D} = \frac {\pi v_{\rm s}}{a} . }[/math]
However, for any chain with greater complexity, including diatomic chains, the associated cut-off frequency and wavelength are not very accurate, since the cut-off wavelength is twice as big and the dispersion relation consists of additional branches, two total for a diatomic chain. It is also not certain from this result whether for higher-dimensional systems the cut-off frequency was accurately predicted by Debye when taking into account the more accurate dispersion relation.
Alternative derivation
For a one-dimensional chain, the formula for the Debye frequency can also be reproduced using a theorem for describing aliasing. The Nyquist–Shannon sampling theorem is used for this derivation, the main difference being that in the case of a one-dimensional chain, the discretization is not in time, but in space.
The cut-off frequency can be determined from the cut-off wavelength. From the sampling theorem, we know that for wavelengths smaller than [math]\displaystyle{ 2a }[/math], or twice the sampling distance, every mode is a repeat of a mode with wavelength larger than [math]\displaystyle{ 2a }[/math], so the cut-off wavelength should be at [math]\displaystyle{ \lambda_{\rm D} = 2 a }[/math]. This results again in [math]\displaystyle{ k_{\rm D} = \frac{2 \pi}{\lambda_D} = \pi / a }[/math], rendering [math]\displaystyle{ \omega_{\rm D} = \frac {\pi v_{\rm s}}{a} . }[/math]
It does not matter which dispersion relation is used, as the same cut-off frequency would be calculated.
See also
- Bose gas
- Gas in a box
- Grüneisen parameter
- Bloch–Grüneisen temperature
- Electrical resistivity and conductivity
References
- ↑ Debye, Peter (1912). "Zur Theorie der spezifischen Waerme" (in de). Annalen der Physik 39 (4): 789–839. doi:10.1002/andp.19123441404. Bibcode: 1912AnP...344..789D. https://zenodo.org/record/1424256.
- ↑ Jump up to: 2.0 2.1 Kittel, Charles (2004). Introduction to Solid State Physics (8 ed.). John Wiley & Sons. ISBN 978-0471415268.
- ↑ Schroeder, Daniel V. "An Introduction to Thermal Physics" Addison-Wesley, San Francisco (2000). Section 7.5
- ↑ Hill, Terrell L. (1960). An Introduction to Statistical Mechanics. Reading, Massachusetts, U.S.A.: Addison-Wesley Publishing Company, Inc.. ISBN 9780486652429. https://archive.org/details/introductiontost0000hill.
- ↑ Oberai, M. M.; Srikantiah, G (1974). A First Course in Thermodynamics. New Delhi, India: Prentice-Hall of India Private Limited. ISBN 9780876920183.
- ↑ Patterson, James D; Bailey, Bernard C. (2007). Solid-State Physics: Introduction to the Theory. Springer. pp. 96–97. ISBN 978-3-540-34933-4.
- ↑ Shulman, L. M. (2004). "The heat capacity of water ice in interstellar or interplanetary conditions". Astronomy and Astrophysics 416: 187–190. doi:10.1051/0004-6361:20031746. Bibcode: 2004A&A...416..187S.
- ↑ Flubacher, P.; Leadbetter, A. J.; Morrison, J. A. (1960). "Heat Capacity of Ice at Low Temperatures". The Journal of Chemical Physics 33 (6): 1751. doi:10.1063/1.1731497. Bibcode: 1960JChPh..33.1751F.
- ↑ In his textbook Kinetic Theory of Liquids (engl. 1947)
- ↑ Bolmatov, D.; Brazhkin, V. V.; Trachenko, K. (2012). "The phonon theory of liquid thermodynamics". Scientific Reports 2: 421. doi:10.1038/srep00421. PMID 22639729. Bibcode: 2012NatSR...2E.421B.
- ↑ Baggioli, M.; Zaccone, A. (2021). "Explaining the specific heat of liquids based on instantaneous normal modes". Physical Review E 104: 014103. doi:10.1103/PhysRevE.104.014103.
- ↑ Debye, P. (1912). "Zur Theorie der spezifischen Wärmen" (in en). Annalen der Physik 344 (14): 789–839. doi:10.1002/andp.19123441404. ISSN 1521-3889. Bibcode: 1912AnP...344..789D. https://zenodo.org/record/1424256.
- ↑ "The one dimensional monatomic solid". https://openphysicslums.files.wordpress.com/2012/08/latticevibrations.pdf.
- ↑ Fitzpatrick, Richard (2006). "Specific heats of solids". http://farside.ph.utexas.edu/teaching/sm1/lectures/node71.html.
- ↑ Jump up to: 15.0 15.1 15.2 Simon, Steven H. (2013-06-20). The Oxford Solid State Basics (First ed.). Oxford: Oxford University Press. ISBN 9780199680764. OCLC 859577633.
- ↑ "The Oxford Solid State Basics" (in en). https://podcasts.ox.ac.uk/series/oxford-solid-state-basics.
- ↑ Srivastava, G. P. (2019-07-16) (in en). The Physics of Phonons. Routledge. ISBN 978-1-351-40955-1. https://books.google.com/books?id=XiCmDwAAQBAJ&q=brillouin+zone+debye+model+book&pg=PA44.
Further reading
- CRC Handbook of Chemistry and Physics, 56th Edition (1975–1976)
- Schroeder, Daniel V. An Introduction to Thermal Physics. Addison-Wesley, San Francisco (2000). Section 7.5.
External links
- Experimental determination of specific heat, thermal and heat conductivity of quartz using a cryostat.
- Simon, Steven H. (2014) The Oxford Solid State Basics (most relevant ones: 1, 2 and 6)
 |