Physics:Magnetic mirror

Short description: Type of nuclear fusion reactor

This shows a basic magnetic mirror machine including a charged particle's motion. The rings in the centre extend the confinement volume horizontally, but are not strictly needed and are not found on many mirror machines.

A magnetic mirror, also known as a magnetic trap or sometimes as a pyrotron, is a type of magnetic confinement fusion device used in fusion power to trap high temperature plasma using magnetic fields. The mirror was one of the earliest major approaches to fusion power, along with the stellarator and z-pinch machines.

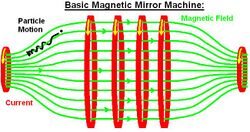
In a classic magnetic mirror, a configuration of electromagnets is used to create an area with an increasing density of magnetic field lines at either end of a confinement volume. Particles approaching the ends experience an increasing force that eventually causes them to reverse direction and return to the confinement area.^[1] This mirror effect will occur only for particles within a limited range of velocities and angles of approach, while those outside the limits will escape, making mirrors inherently "leaky".

An analysis of early fusion devices by Edward Teller pointed out that the basic mirror concept is inherently unstable. In 1960, Soviet researchers introduced a new "minimum-B" configuration to address this, which was then modified by UK researchers into the "baseball coil" and by the US to "yin-yang magnet" layout. Each of these introductions led to further increases in performance, damping out various instabilities, but requiring ever-larger magnet systems. The tandem mirror concept, developed in the US and Russia at about the same time, offered a way to make energy-positive machines without requiring enormous magnets and power input.

By the late 1970s, many of the design problems were considered solved, and Lawrence Livermore Laboratory began the design of the Mirror Fusion Test Facility (MFTF) based on these concepts. The machine was completed in 1986, but by this time, experiments on the smaller Tandem Mirror Experiment revealed new problems. In a round of budget cuts, MFTF was mothballed, and eventually scrapped. A fusion reactor concept called the Bumpy torus made use of a series of magnetic mirrors joined in a ring. It was investigated at the Oak Ridge National Laboratory until 1986.^[2] The mirror approach has since seen less development, in favor of the tokamak, but mirror research continues today in countries like Japan and Russia.^[3]

History

Early work

Lawrence Livermore's Q-cumber device, seen in 1955 when it was still classified. It was among the first to clearly demonstrate confinement using the mirror effect.

The concept of magnetic-mirror plasma confinement was proposed in the early-1950s independently by Gersh Budker^[4] at the Kurchatov Institute, Russia and Richard F. Post at the Lawrence Livermore National Laboratory in the US.^[5]

With the formation of Project Sherwood in 1951, Post began the development of a small device to test the mirror configuration. This consisted of a linear pyrex tube with magnets around the outside. The magnets were arranged in two sets, one set of small magnets spaced evenly along the length of the tube, and another pair of much larger magnets at either end. In 1952 they were able to demonstrate that plasma within the tube was confined for much longer times when the mirror magnets at the end were turned on. At the time, he referred to this device as the "pyrotron", but this name did not catch on.

Instabilities

In a now-famous talk on fusion in 1954, Edward Teller noted that any device with convex magnetic field lines would likely be unstable, a problem today known as the flute instability.^[6] The mirror has precisely such a configuration; the magnetic field was highly convex at the ends where the field strength increased.^{[lower-alpha 1]} This led to serious concern by Post, but over the next year, his team could find no sign of these problems. In October 1955 he went so far as to state that "it is now becoming clear that in the case of the mirror machine at least these calculations do not apply in detail."^[7]

In Russia, the first small-scale mirror ("probkotron") was built in 1959 at the Budker Institute of Nuclear Physics in Novosibirsk, Russia. They immediately saw the problem Teller had warned about. This led to something of a mystery, as the US teams under Post continued to lack any evidence of such problems. In 1960, Post and Marshall Rosenbluth published a report "providing evidence for the existence of a stability confined plasma... where the simplest hydromagnetic theory predicts instability."^[8]

At a meeting on plasma physics in Saltzberg in 1961, the Soviet delegation presented considerable data showing the instability, while the US teams continued to show none. An offhand question by Lev Artsimovich settled the matter; when he asked if the charts being produced from the instruments in the US machines were adjusted for a well-known delay in the output of the detectors being used, it suddenly became clear that the apparent 1 ms stability was, in fact, a 1 ms delay in the measurements.^[9] Artsimovich went so far as to claim "we now do not have a single experimental fact indicating long and stable confinement of plasma with hot ions within a simple magnetic mirror geometry."^[10]

New geometries

The Baseball II was a superconducting version of the baseball coil design, seen here in 1969 during construction.

The 1978 2X magnetic bottle experiment. Fred Coensgen is pictured. The cylinder holds one set of neutral beam injectors, the mirror itself is not visible.

The issue of the potential instabilities had been considered in the field for some time and a number of possible solutions had been introduced. These generally worked by changing the shape of the magnetic field so it was concave everywhere, the so-called "minimum-B" configuration.^[10]

At the same 1961 meeting, Mikhail Ioffe introduced data from a minimum-B experiment. His design used a series of six additional current-carrying bars in the interior of an otherwise typical mirror to bend the plasma into the shape of a twisted bow-tie to produce a minimum-B configuration. They demonstrated that this greatly improved the confinement times to the order of milliseconds. Today this arrangement is known as "Ioffe bars".^[10]

A group at the Culham Centre for Fusion Energy noted that Ioffe's arrangement could be improved by combining the original rings and the bars into a single new arrangement similar to the seam on a tennis ball. This concept was picked up in the US where it was renamed after the stitching on a baseball. These "baseball coils" had the great advantage that they left the internal volume of the reactor open, allowing easy access for diagnostic instruments. On the downside, the size of the magnet in comparison to the volume of plasma was inconvenient and required very powerful magnets. Post later introduced a further improvement, the "yin-yang coils", which used two C-shaped magnets to produce the same field configuration, but in a smaller volume.

In the US, major changes to the fusion program were underway. Robert Hirsch and his assistant Stephen O. Dean were excited by the huge performance advance seen in the Soviet tokamaks, which suggested power production was now a real possibility. Hirsch began to change the program from one he derided as a series of uncoordinated science experiments into a planned effort to ultimately reach breakeven. As part of this change, he began to demand that the current systems demonstrate real progress or they would be cancelled. The bumpy torus, levitron and Astron were all abandoned, not without a fight.^[11]

Dean met with Livermore's team and made it clear that Astron would likely be cut, and mirrors had to improve or face cutting as well, which would have left the lab with no major fusion projects. In December 1972, Dean met with the mirror team and made a series of demands; their systems would have to demonstrate an nT value of 10¹², compared to the current best number on 2XII of 8x10⁹. After considerable concern from the researchers that this would be impossible, Dean backed off to 10¹¹ being demonstrated by the end of 1975.^[11]

DCLC

Although 2XII was nowhere near the level needed by Dean's demands, it was nevertheless extremely successful in demonstrating that the yin-yang arrangement was workable and suppressed the major instabilities seen in earlier mirrors. But as experiments continued through 1973, the results were not improving as expected. Plans emerged to brute-force the performance through the addition of neutral-beam injection to quickly raise the temperature to reach Dean's conditions. The result was 2XIIB, the B for "beams".^[12]

While 2XIIB was being set up, in November 1974, Fowler received a letter from Ioffe containing a series of photographs of oscilloscope traces with no other explanation. Fowler realized they demonstrated that injecting warm plasma during the run improved confinement. This appeared to be due to a long-expected but so-far unseen instability known as "drift-cyclotron loss-cone", or DCLC.^[13] Ioffe's photographs demonstrated that DCLC was being seen in Soviet reactors and that warm plasma appeared to stabilize it.^[14]

2XIIB reactor started real experiments in 1975, and significant DCLC was immediately seen. Annoyingly, the effect grew stronger as they improved the operating conditions with better vacuum and cleaning of the interior. Fowler recognized the performance was identical to that of Ioffe's photographs, and 2XIIB was modified to inject warm plasma during the center of the run. When the results were seen, they were described as "sunlight was breaking through the clouds and there was the chance that everything would be all right."^[15]

Q-enhancement and tandem mirrors

The Tandem Mirror Experiment (TMX) in 1979. One of the two yin-yang mirrors can be seen exposed on the end closer to the camera.

In July 1975, the 2XIIB team presented their results for nT at 7x10¹⁰, an order of magnitude better than 2XII and close enough to Dean's requirements.^[15] By this time, the Princeton Large Torus had come online and was setting record after record, prompting Hirsch to begin planning for even larger machines for the early 1980s with the explicit goal of hitting breakeven, or Q=1. This became known as the Tokamak Fusion Test Reactor (TFTR), whose goal was to run on deuterium-tritium fuel and reach Q=1, while future machines would be Q>10.^[16]

With the latest results on 2XIIB, it appeared that a larger yin-yang design would also improve performance. However, calculations showed it would only reach Q=0.03. Even the most developed versions of the basic concept, with leakage at the absolute lower limit allowed by theory, could only reach Q=1.2. This made these designs largely useless for power production, and Hirsch demanded that this be improved if the program were to continue. This problem became known as "Q-enhancement".^[16]

In March 1976, the Livermore team decided to organize a working group on the topic of Q-enhancement at the October 1976 international fusion meeting in Germany. Over the July 4th weekend, Fowler and Post came up with the idea of the tandem mirror, a system consisting of two mirrors at either end of a large chamber that held large amounts fusion fuel at lower magnetic pressure. They returned to LLNL on Monday to find the idea had been developed independently by a staff physicist, Grant Logan. They brought further developed versions of these ideas to Germany to find a Soviet researcher proposing exactly the same solution.^[17]

Upon their return from the meeting, Dean met with the team and decided to shut down the Baseball II system and direct its funding to a tandem mirror project. This emerged as the Tandem Mirror Experiment, or TMX.^[18] The final design was presented and approved in January 1977. Construction of what was then the largest experiment at Livermore was completed by October 1978. By July 1979, experiments were demonstrating that TMX was operating as expected.^[19]

Thermal barriers and MFTF

Even before the tandem mirror concept emerged, what was by this time the Department of Energy had agreed to fund the construction of a much larger mirror known as the Mirror Fusion Test Facility (MFTF). At the time, the plan for MFTF was to simply be the largest yin-yang magnet anyone could figure out how to build. With the success of the TMX concept, the design was modified to become MFTF-B, using two of the largest yin-yang magnets anyone could figure out how to build in an enormous tandem configuration. The goal was to meet Q=5. Through late 1978 when the teams began to actually consider the steps in scaling up the TMX, it became clear that it simply would not hit the required goals.^[20] In January 1979, Fowler stopped the work, stating that some improvement would have to be found.^[21]

During experiments on the TMX, it was found to everyone's surprise that the law introduced by Lyman Spitzer in the 1950s was not holding; in TMX at least, electrons on any single magnetic line were found to be in a wide variety of speeds, which was entirely unexpected. Further work by John Clauser demonstrated that this was due to the warm plasma injection used to suppress DCLC. Logan took these results and used them to come up with an entirely new way to confine the plasma; with the careful arrangement of these electrons, one could produce a region with a large number of "cool" electrons that would attract the positively charged ions. Dave Baldwin then demonstrated this could be enhanced through the neutral beams. Fowler referred to the result as a "thermal barrier", as the hotter fuel was repelled from these regions. It appeared it could maintain confinement using much less energy than the pure TMX concept.^[22]

This result suggested that MFTF would not just meet an arbitrary Q=5, but make it a real competitor to the tokamaks, which were promising much higher Q values. Fowler began the design of another version of MFTF, still called MFTF-B, based on the thermal barrier concept. the lab decided they should begin construction, lacking any experimental evidence that the concept worked, in order to get a competitive machine out around the same time as TFTR. While this huge machine was being built, TMX would be modified to test the concept.^[23]

On 28 January 1980, Fowler and his team presented their results to the DOE. Demonstrating that TMX had worked, and armed with additional data from the Soviets as well as computer simulations, they presented a plan to begin construction on a $226 million MFTF while upgrading TMX to add the thermal barriers in the $14 million TMX-U. The proposal was accepted and construction on both systems began, with TMX shutting down in September 1980 for conversion.^[24]

TMX-U fails, MFTF mothballed

The MFTF was a $372 million Livermore project that was mothballed

TMX-U began experiments in July 1982, by which time parts of Boeing 747-sized MFTF were being installed at Building 431.^[25] However, as they attempted to raise the density of the plasma to values that would be needed for MFTF, they found that plasma escaping from the central tank overwhelmed the thermal barriers. There was no obvious reason to believe the same would not occur on the MFTF. If the rates seen in TMX-U were typical, there was no way MFTF would come remotely close to its Q goals.^[26]

Construction on MFTF, already budgeted, continued and the system was declared officially complete on 21 February 1986, at a final price of $372 million. While thanking the team for their contributions in building the system, the new director of the DOE, John Clarke, also announced that there would be no funding to run it.^[27] Clarke later lamented that the decision to cancel the project was very difficult, "It would have been so much easier if I had a technical failure to point to."^[26]

It sat unused for a year on the chance that operational funding would be provided. It never was. The machine was scrapped in 1987. The DOE also cut funding for most other mirror programs.^[27]

After 1986

The Gas Dynamic Trap in Russia.

Magnetic mirror research continued in Russia, one modern example is the Gas Dynamic Trap, an experimental fusion machine used at the Budker Institute of Nuclear Physics in Akademgorodok (Academic Town) in Novosibirsk (New Siberia), Russia. This machine has achieved a 0.6 beta ratio for 5E-3 seconds, at a low temperature of 1 KeV.

The concept had a number of technical challenges including maintaining the non-Maxwellian velocity distribution. This meant that instead of many high energy ions hitting one another, the ion energy spread out into a bell curve. The ions then thermalized, leaving most of the material too cold to fuse. Collisions also scattered the charged particles so much that they could not be contained. Lastly, velocity space instabilities contributed to the escape of the plasma.^{[citation needed]}

In September 2022, University of Wisconsin–Madison researchers incorporated a spin-off startup company named Realta Fusion to develop and commercialize tandem mirror reactors to supply industrial process heat with smaller power plants. Their stated goal is a “lowest capital, least complex path” to fusion energy.^[28]^[29]^[30] In May 2023, United States Department of Energy granted the company additional funding.^[31]

Magnetic mirrors play an important role in other types of magnetic fusion energy devices such as tokamaks, where the toroidal magnetic field is stronger on the inboard side than on the outboard side. The resulting effects are known as neoclassical. Magnetic mirrors also occur in nature. Electrons and ions in the magnetosphere, for example, will bounce back and forth between the stronger fields at the poles, leading to the Van Allen radiation belts.^{[citation needed]}

Mathematical derivation

The mirror effect can be shown mathematically. Assume adiabatic invariance of the magnetic moment, i.e. that the particle's magnetic moment and total energy do not change.^[32] Adiabatic invariance is lost when a particle occupies a null point or zone of no magnetic field.^[33] The magnetic moment can be expressed as: [math]\displaystyle{ \mu=\frac{m v_{\perp}^2}{2 B} }[/math]

It is assumed that μ will remain constant while the particle moves into the denser magnetic field. Mathematically, for this to happen the velocity perpendicular to the magnetic field [math]\displaystyle{ v_{\perp} }[/math] must also rise. Meanwhile the total energy of the particle [math]\displaystyle{ \mathcal{E} }[/math] can be expressed as: [math]\displaystyle{ \mathcal{E} = q\phi + \tfrac{1}{2} m v_{\parallel}^2 + \tfrac{1}{2} m v_{\perp}^2 }[/math]

In regions with no electric field, if the total energy remains constant then the velocity parallel to the magnetic field must drop. If it can go negative then there is a motion repelling the particle from the dense fields.^{[citation needed]}

Mirror ratios

Magnetic mirrors themselves have a mirror ratio this is expressed mathematically as:^[34] [math]\displaystyle{ r_\text{mirror} = \frac{B_\text{max}}{B_\text{min}} }[/math]

At the same time, particles within the mirror have a pitch angle. This is the angle between the particles' velocity vector and the magnetic field vector.^[35] Surprisingly, the particles with the small pitch angle can escape the mirror.^[36] These particles are said to be in the loss cone. The reflected particles meet the following criteria:^[37] [math]\displaystyle{ \frac{v_\perp}{v} \gt \frac{1}{\sqrt{r_\text{mirror}}} }[/math]

Where [math]\displaystyle{ v_\perp }[/math] is the particle velocity perpendicular to the magnetic field and [math]\displaystyle{ v }[/math] is the particle speed.

This result was surprising because it was expected that heavier and faster particles, or those with less electric charge, would be harder to reflect. It was also expected that a smaller magnetic field would reflect fewer particles. However, the gyroradius in those circumstances is also larger, so that the radial component of the magnetic field seen by the particle is also larger. It is true that the minimum volume and magnetic energy is larger for the case of fast particles and weak fields, but the mirror ratio required remains the same.

Adiabatic invariance

The properties of magnetic mirrors can be derived using the adiabatic invariance of magnetic flux under changes in magnetic field strength. As the field gets stronger, the velocity increases proportionally to the square root of B, and the kinetic energy is proportional to B. This can be thought of as an effective potential binding the particle.^{[citation needed]}

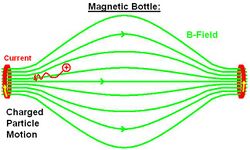
Magnetic bottles

This image shows how a charged particle will corkscrew along the magnetic fields inside a magnetic bottle, which is two magnetic mirrors placed close together. The particle can be reflected from the dense field region and will be trapped.

A magnetic bottle is two magnetic mirrors placed close together. For example, two parallel coils separated by a small distance, carrying the same current in the same direction will produce a magnetic bottle between them. Unlike the full mirror machine which typically had many large rings of current surrounding the middle of the magnetic field, the bottle typically has just two rings of current. Particles near either end of the bottle experience a magnetic force towards the center of the region; particles with appropriate speeds spiral repeatedly from one end of the region to the other and back. Magnetic bottles can be used to temporarily trap charged particles. It is easier to trap electrons than ions, because electrons are so much lighter.^[38] This technique is used to confine the high energy of plasma in fusion experiments.

In a similar way, the Earth's non-uniform magnetic field traps charged particles coming from the Sun in doughnut shaped regions around the Earth called the Van Allen radiation belts, which were discovered in 1958 using data obtained by instruments aboard the Explorer 1 satellite.

Biconic cusps

A biconic cusp

Main page: Physics:Biconic cusp

If one of the poles in the magnetic bottle is reversed, it becomes a biconic cusp, which can also hold charged particles.^[39]^[40]^[41] Biconic cusps were first studied by Harold Grad at the Courant Institute, studies reveal the presence of different types of particles inside a biconic cusp. The most financed cusp approach is the Compact Fusion Reactor which was supported by Lockheed-Martin starting in 2007.^[42]

Notes

↑ This convexity can be seen in the diagram at the top of this article.

References

Citations

↑ Fitzpatrick, Richard. "Magnetic Mirrors." Home Page for Richard Fitzpatrick. The University of Texas at Austin, 31 Mar. 2011. Web. 19 July 2011.
↑ Uckan; Dandl; Hendrick; Bettis; Lidsky; McAlees; Santoro; Watts et al. (January 1977). The Elmo Bumpy Torus (EBT) Reactor. Oak Ridge National Laboratory. https://www.osti.gov/scitech/servlets/purl/5233224-ix7xa6. Retrieved June 1, 2017.
↑ T.C. Simonen, Three game changing discoveries: a simpler fusion concept? J. Fusion Energ., February 2016, Volume 35, Issue 1, pp 63-68. doi:10.1007/s10894-015-0017-2
↑ In Russian: Г.И. Будкер, Физика плазмы и проблема управляемых термоядерных реакций, Т. 3, Изд. АН СССР, Москва (1958), стр. 3-31; in English: G. I. Budker, Plasma Physics and the Problem of Controlled Thermonuclear Reactions, Vol. 3, Pergamon Press, New York (1959), pp. 1-33
↑ "R. F. Post, Proc. of Second U.N. Int. Conf. on Peaceful Uses of Atomic Energy, Vol. 32, Paper A/Conf. 15/P/377, Geneva (1958), pp. 245-265". http://www-naweb.iaea.org/napc/physics/2ndgenconf/data/Proceedings%201958/papers%20Vol32/Paper31_Vol32.pdf.
↑ Herman (2006), p. 30.
↑ Bromberg 1982, p. 58.
↑ Bromberg 1982, p. 108.
↑ Bromberg 1982, p. 110.
↑ ^10.0 ^10.1 ^10.2 Bromberg 1982, p. 111.
↑ ^11.0 ^11.1 Heppenheimer 1984, p. 78.
↑ Heppenheimer 1984, p. 79.
↑ Heppenheimer 1984, p. 80.
↑ Heppenheimer 1984, p. 81.
↑ ^15.0 ^15.1 Heppenheimer 1984, p. 82.
↑ ^16.0 ^16.1 Heppenheimer 1984, p. 85.
↑ Heppenheimer 1984, p. 89.
↑ "TMX Major Project proposal" Fred Coensgen, January 12, 1977
↑ Heppenheimer 1984, p. 91.
↑ "Summary of results from the tandem mirror experiment, TMX group, February 26, 1981
↑ Heppenheimer 1984, p. 93.
↑ Heppenheimer 1984, p. 95.
↑ Heppenheimer 1984, p. 96.
↑ Heppenheimer 1984, p. 97.
↑ Heppenheimer 1984, p. 201.
↑ ^26.0 ^26.1 Booth 1987, p. 155.
↑ ^27.0 ^27.1 Booth 1987, p. 152.
↑ Furlong, Kieran (June 29, 2022). Realta Fusion: Breakthrough physics for clean energy generation. Wisconsin Energy Institute, University of Wisconsin, Madison – via YouTube.
↑ "Realta Fusion". Wisconsin Energy Institute, University of Wisconsin, Madison (Press release). 2021. Retrieved 23 January 2023.
↑ Moe, Alex (September 19, 2022). "Fusion startup aims to help offset greenhouse gas emissions". WisBusiness.com. https://www.wisbusiness.com/2022/fusion-startup-aims-to-help-offset-greenhouse-gas-emissions/.
↑ Wang, Brian (2023-05-31). "Eight Nuclear Fusion Companies Get a Total of $46 Million | NextBigFuture.com" (in en-US). https://www.nextbigfuture.com/2023/05/eight-nuclear-fusion-companies-get-a-total-of-46-million.html.
↑ F. Chen, Introduction to Plasma Physics and Controlled Fusion (Plenum, New York, 1984), Vol. 1, pp. 30–34. ISBN:978-0-306-41332-2
↑ TG Northrop, "The Adiabatic Motion of Charged Particles" (Interscience, New York, 1963)
↑ "Particle Loss Rates from Electrostatic Wells of Arbitrary Mirror Ratios." Physics of Fluids 28.1 (1985): 352-57. Web. 15.
↑ Dolan, T. J. "Magnetic Electrostatic Plasma Confinement." Plasma Physics and Controlled Fusion 36 (1994): 1539-593. Print.
↑ G Gibson, Willard C Jordan, Eugene Lauer, Physical Review Letters, 5: 141 (1960)
↑ Principals of Plasma Physics, N Krall, 1973, Page 267
↑ "A biased probe analysis of potential well formation in an electron only, low beta Polywell magnetic field" Physics of Plasma, May 9, 2013, Vol 20, 052504
↑ The motion of a charged particle near a zero field point (in english). New York: New York University: Courant Institute of Mathematical Sciences,. 1961.
↑ Grad, H. (December 1, 1957). Theory of Cusped Geometries, I. General Survey, NYO-7969 (Report). Institute of Mathematical Sciences, New York University.
↑ Berowitz; Grad, H.; Rubin, H. (1958). Proceedings of the second United Nations International conference on peaceful uses of atomic energy (Report). 31. Geneva. p. 177.
↑ McGuire, Thomas (6 August 2015). The Lockheed Martin Compact Fusion Reactor; Thursday Colloquium Lecture (Report). Princeton University, Princeton.