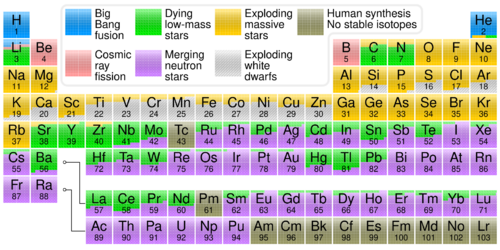
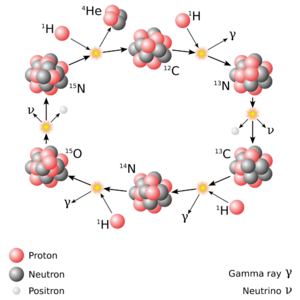Physics:Stellar nucleosynthesis

From HandWiki
Logarithm of the relative energy output (ε) of proton–proton (PP), CNO and Triple-α fusion processes at different temperatures (T). The dashed line shows the combined energy generation of the PP and CNO processes within a star. At the Sun's core temperature, the PP process is more efficient.
Short description: Creation of chemical elements within stars

Stellar nucleosynthesis is the creation (nucleosynthesis) of chemical elements by nuclear fusion reactions within stars. Stellar nucleosynthesis has occurred since the original creation of hydrogen, helium and lithium during the Big Bang. As a predictive theory, it yields accurate estimates of the observed abundances of the elements. It explains why the observed abundances of elements change over time and why some elements and their isotopes are much more abundant than others. The theory was initially proposed by Fred Hoyle in 1946,[1] who later refined it in 1954.[2] Further advances were made, especially to nucleosynthesis by neutron capture of the elements heavier than iron, by Margaret and Geoffrey Burbidge, William Alfred Fowler and Fred Hoyle in their famous 1957 B2FH paper,[3] which became one of the most heavily cited papers in astrophysics history.

Stars evolve because of changes in their composition (the abundance of their constituent elements) over their lifespans, first by burning hydrogen (main sequence star), then helium (horizontal branch star), and progressively burning higher elements. However, this does not by itself significantly alter the abundances of elements in the universe as the elements are contained within the star. Later in its life, a low-mass star will slowly eject its atmosphere via stellar wind, forming a planetary nebula, while a higher–mass star will eject mass via a sudden catastrophic event called a supernova. The term supernova nucleosynthesis is used to describe the creation of elements during the explosion of a massive star or white dwarf.

The advanced sequence of burning fuels is driven by gravitational collapse and its associated heating, resulting in the subsequent burning of carbon, oxygen and silicon. However, most of the nucleosynthesis in the mass range A = 28–56 (from silicon to nickel) is actually caused by the upper layers of the star collapsing onto the core, creating a compressional shock wave rebounding outward. The shock front briefly raises temperatures by roughly 50%, thereby causing furious burning for about a second. This final burning in massive stars, called explosive nucleosynthesis or supernova nucleosynthesis, is the final epoch of stellar nucleosynthesis.

A stimulus to the development of the theory of nucleosynthesis was the discovery of variations in the abundances of elements found in the universe. The need for a physical description was already inspired by the relative abundances of the chemical elements in the solar system. Those abundances, when plotted on a graph as a function of the atomic number of the element, have a jagged sawtooth shape that varies by factors of tens of millions (see history of nucleosynthesis theory).[4] This suggested a natural process that is not random. A second stimulus to understanding the processes of stellar nucleosynthesis occurred during the 20th century, when it was realized that the energy released from nuclear fusion reactions accounted for the longevity of the Sun as a source of heat and light.[5]

History

In 1920, Arthur Eddington proposed that stars obtained their energy from nuclear fusion of hydrogen to form helium and also raised the possibility that the heavier elements are produced in stars.

In 1920, Arthur Eddington, on the basis of the precise measurements of atomic masses by F.W. Aston and a preliminary suggestion by Jean Perrin, proposed that stars obtained their energy from nuclear fusion of hydrogen to form helium and raised the possibility that the heavier elements are produced in stars.[6][7][8] This was a preliminary step toward the idea of stellar nucleosynthesis. In 1928 George Gamow derived what is now called the Gamow factor, a quantum-mechanical formula yielding the probability for two contiguous nuclei to overcome the electrostatic Coulomb barrier between them and approach each other closely enough to undergo nuclear reaction due to the strong nuclear force which is effective only at very short distances.[9]:410 In the following decade the Gamow factor was used by Atkinson and Houtermans and later by Edward Teller and Gamow himself to derive the rate at which nuclear reactions would occur at the high temperatures believed to exist in stellar interiors.

In 1939, in a Nobel lecture entitled "Energy Production in Stars", Hans Bethe analyzed the different possibilities for reactions by which hydrogen is fused into helium.[10] He defined two processes that he believed to be the sources of energy in stars. The first one, the proton–proton chain reaction, is the dominant energy source in stars with masses up to about the mass of the Sun. The second process, the carbon–nitrogen–oxygen cycle, which was also considered by Carl Friedrich von Weizsäcker in 1938, is more important in more massive main-sequence stars.[11]:167 These works concerned the energy generation capable of keeping stars hot. A clear physical description of the proton–proton chain and of the CNO cycle appears in a 1968 textbook.[12]:365 Bethe's two papers did not address the creation of heavier nuclei, however. That theory was begun by Fred Hoyle in 1946 with his argument that a collection of very hot nuclei would assemble thermodynamically into iron.[1] Hoyle followed that in 1954 with a paper describing how advanced fusion stages within massive stars would synthesize the elements from carbon to iron in mass.[2][13]

Hoyle's theory was extended to other processes, beginning with the publication of the 1957 review paper "Synthesis of the Elements in Stars" by Burbidge, Burbidge, Fowler and Hoyle, more commonly referred to as the B2FH paper.[3] This review paper collected and refined earlier research into a heavily cited picture that gave promise of accounting for the observed relative abundances of the elements; but it did not itself enlarge Hoyle's 1954 picture for the origin of primary nuclei as much as many assumed, except in the understanding of nucleosynthesis of those elements heavier than iron by neutron capture. Significant improvements were made by Alastair G. W. Cameron and by Donald D. Clayton. In 1957 Cameron presented his own independent approach to nucleosynthesis,[14] informed by Hoyle's example, and introduced computers into time-dependent calculations of evolution of nuclear systems. Clayton calculated the first time-dependent models of the s-process in 1961[15] and of the r-process in 1965,[16] as well as of the burning of silicon into the abundant alpha-particle nuclei and iron-group elements in 1968,[17][18] and discovered radiogenic chronologies[19] for determining the age of the elements.

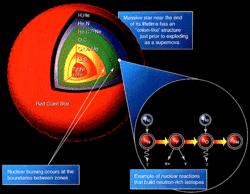
Cross section of a supergiant showing nucleosynthesis and elements formed.

Key reactions

A version of the periodic table indicating the origins – including stellar nucleosynthesis – of the elements.

The most important reactions in stellar nucleosynthesis:

Hydrogen fusion

Main pages: Astronomy:Proton–proton chain reaction, Astronomy:CNO cycle, and Astronomy:Deuterium fusion
Proton–proton chain reaction
CNO-I cycle
The helium nucleus is released at the top-left step.

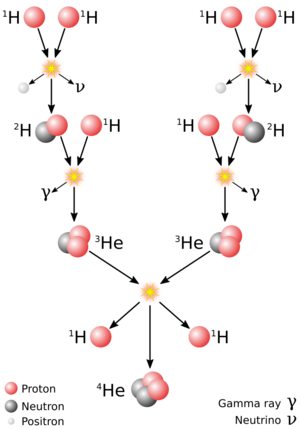
Hydrogen fusion (nuclear fusion of four protons to form a helium-4 nucleus[20]) is the dominant process that generates energy in the cores of main-sequence stars. It is also called "hydrogen burning", which should not be confused with the chemical combustion of hydrogen in an oxidizing atmosphere. There are two predominant processes by which stellar hydrogen fusion occurs: proton–proton chain and the carbon–nitrogen–oxygen (CNO) cycle. Ninety percent of all stars, with the exception of white dwarfs, are fusing hydrogen by these two processes.[21]:245

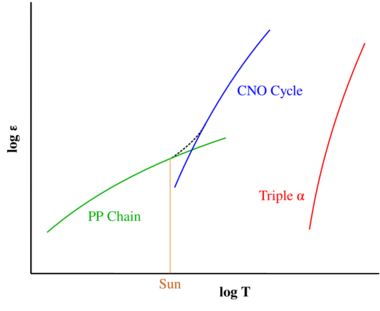
In the cores of lower-mass main-sequence stars such as the Sun, the dominant energy production process is the proton–proton chain reaction. This creates a helium-4 nucleus through a sequence of reactions that begin with the fusion of two protons to form a deuterium nucleus (one proton plus one neutron) along with an ejected positron and neutrino.[22] In each complete fusion cycle, the proton–proton chain reaction releases about 26.2 MeV.[22] The proton–proton chain reaction cycle is relatively insensitive to temperature; a 10% rise of temperature would increase energy production by this method by 46%, hence, this hydrogen fusion process can occur in up to a third of the star's radius and occupy half the star's mass. For stars above 35% of the Sun's mass,[23] the energy flux toward the surface is sufficiently low and energy transfer from the core region remains by radiative heat transfer, rather than by convective heat transfer.[24] As a result, there is little mixing of fresh hydrogen into the core or fusion products outward.

In higher-mass stars, the dominant energy production process is the CNO cycle, which is a catalytic cycle that uses nuclei of carbon, nitrogen and oxygen as intermediaries and in the end produces a helium nucleus as with the proton–proton chain.[22] During a complete CNO cycle, 25.0 MeV of energy is released. The difference in energy production of this cycle, compared to the proton–proton chain reaction, is accounted for by the energy lost through neutrino emission.[22] The CNO cycle is very temperature sensitive, a 10% rise of temperature would produce a 350% rise in energy production. About 90% of the CNO cycle energy generation occurs within the inner 15% of the star's mass, hence it is strongly concentrated at the core.[25] This results in such an intense outward energy flux that convective energy transfer becomes more important than does radiative transfer. As a result, the core region becomes a convection zone, which stirs the hydrogen fusion region and keeps it well mixed with the surrounding proton-rich region.[26] This core convection occurs in stars where the CNO cycle contributes more than 20% of the total energy. As the star ages and the core temperature increases, the region occupied by the convection zone slowly shrinks from 20% of the mass down to the inner 8% of the mass.[25] The Sun produces on the order of 1% of its energy from the CNO cycle.[27][lower-alpha 1][28]:357[29][lower-alpha 2]

The type of hydrogen fusion process that dominates in a star is determined by the temperature dependency differences between the two reactions. The proton–proton chain reaction starts at temperatures about 4×106 K,[30] making it the dominant fusion mechanism in smaller stars. A self-maintaining CNO chain requires a higher temperature of approximately 16×106 K, but thereafter it increases more rapidly in efficiency as the temperature rises, than does the proton–proton reaction.[31] Above approximately 17×106 K, the CNO cycle becomes the dominant source of energy. This temperature is achieved in the cores of main-sequence stars with at least 1.3 times the mass of the Sun.[32] The Sun itself has a core temperature of about 15.7×106 K.[33]:5 As a main-sequence star ages, the core temperature will rise, resulting in a steadily increasing contribution from its CNO cycle.[25]

Helium fusion

Main pages: Astronomy:Triple-alpha process and Astronomy:Alpha process

Main sequence stars accumulate helium in their cores as a result of hydrogen fusion, but the core does not become hot enough to initiate helium fusion. Helium fusion first begins when a star leaves the red giant branch after accumulating sufficient helium in its core to ignite it. In stars around the mass of the Sun, this begins at the tip of the red giant branch with a helium flash from a degenerate helium core, and the star moves to the horizontal branch where it burns helium in its core. More massive stars ignite helium in their core without a flash and execute a blue loop before reaching the asymptotic giant branch. Such a star initially moves away from the AGB toward bluer colours, then loops back again to what is called the Hayashi track. An important consequence of blue loops is that they give rise to classical Cepheid variables, of central importance in determining distances in the Milky Way and to nearby galaxies.[34]:250 Despite the name, stars on a blue loop from the red giant branch are typically not blue in colour but are rather yellow giants, possibly Cepheid variables. They fuse helium until the core is largely carbon and oxygen. The most massive stars become supergiants when they leave the main sequence and quickly start helium fusion as they become red supergiants. After the helium is exhausted in the core of a star, helium fusion will continue in a shell around the carbon–oxygen core.[20][24]

In all cases, helium is fused to carbon via the triple-alpha process, i.e., three helium nuclei are transformed into carbon via 8Be.[35]:30 This can then form oxygen, neon, and heavier elements via the alpha process. In this way, the alpha process preferentially produces elements with even numbers of protons by the capture of helium nuclei. Elements with odd numbers of protons are formed by other fusion pathways.

Reaction rate

The reaction rate density between species A and B, having number densities nA,B, is given by:

[math]\displaystyle{ r = n_A \, n_B \, k }[/math]

where k is the reaction rate constant of each single elementary binary reaction composing the nuclear fusion process:

[math]\displaystyle{ k = \langle \sigma(v)\,v \rangle }[/math]

here, σ(v) is the cross-section at relative velocity v, and averaging is performed over all velocities.

Semi-classically, the cross section is proportional to [math]\displaystyle{ \pi\,\lambda^2 }[/math], where [math]\displaystyle{ \lambda = h/p }[/math] is the de Broglie wavelength. Thus semi-classically the cross section is proportional to [math]\displaystyle{ \frac{m}{E} }[/math].

However, since the reaction involves quantum tunneling, there is an exponential damping at low energies that depends on Gamow factor EG, giving an Arrhenius equation:

[math]\displaystyle{ \sigma(E) = \frac{S(E)}{E} e^{-\sqrt{\frac{E_\text{G}}{E}}} }[/math]

where S(E) depends on the details of the nuclear interaction, and has the dimension of an energy multiplied for a cross section.

One then integrates over all energies to get the total reaction rate, using the Maxwell–Boltzmann distribution and the relation:

[math]\displaystyle{ \frac{r}{V} = n_A n_B \int_0^{\infty}\frac{S(E)}{E} \, e^{-\sqrt{\frac{E_\text{G}}{E}}} 2\sqrt{\frac{E}{\pi(kT)^3}} e^{-\frac{E}{kT}} \,\sqrt{\frac{2E}{m_\text{R}}}dE }[/math]

where [math]\displaystyle{ m_\text{R} = \frac{m_1 m_2}{m_1 + m_2} }[/math] is the reduced mass.

Since this integration has an exponential damping at high energies of the form [math]\displaystyle{ \sim e^{-\frac{E}{kT}} }[/math] and at low energies from the Gamow factor, the integral almost vanished everywhere except around the peak, called Gamow peak,[36]:185 at E0, where:

[math]\displaystyle{ \frac{\partial}{\partial E} \left( -\sqrt{\frac{E_\text{G}}{E}} - \frac{E}{kT}\right) \, = \, 0 }[/math]

Thus:

[math]\displaystyle{ E_0 = \left(\frac{1}{2}kT \sqrt{E_\text{G}}\right)^\frac{2}{3} }[/math]

The exponent can then be approximated around E0 as:

[math]\displaystyle{ e^{-\frac{E}{kT} - \sqrt{\frac{E_\text{G}}{E}}} \approx e^{-\frac{3E_0}{kT}} \exp\left(-\frac{(E - E_0)^2}{\frac{4}{3} E_0 kT}\right) }[/math]

And the reaction rate is approximated as:[37]

[math]\displaystyle{ \frac{r}{V} \approx n_A \, n_B \, \frac{4\sqrt{2}}{\sqrt{3 m_\text{R}}}\, \sqrt{E_0} \frac{S(E_0)}{kT} e^{-\frac{3E_0}{kT}} }[/math]

Values of S(E0) are typically 10−3 – 103 keV·b, but are damped by a huge factor when involving a beta decay, due to the relation between the intermediate bound state (e.g. diproton) half-life and the beta decay half-life, as in the proton–proton chain reaction. Note that typical core temperatures in main-sequence stars give kT of the order of keV.[38]:ch. 3

Thus, the limiting reaction in the CNO cycle, proton capture by 147N, has S(E0) ~ S(0) = 3.5 keV·b, while the limiting reaction in the proton–proton chain reaction, the creation of deuterium from two protons, has a much lower S(E0) ~ S(0) = 4×10−22 keV·b.[39][40] Incidentally, since the former reaction has a much higher Gamow factor, and due to the relative abundance of elements in typical stars, the two reaction rates are equal at a temperature value that is within the core temperature ranges of main-sequence stars.[41]:211

References

Notes

  1. ↑ Particle physicist Andrea Pocar points out, "Confirmation of CNO burning in our sun, where it operates at only one percent, reinforces our confidence that we understand how stars work."
  2. ↑ "This result therefore paves the way toward a direct measurement of the solar metallicity using CNO neutrinos. Our findings quantify the relative contribution of CNO fusion in the Sun to be of the order of 1 per cent."—M. Agostini, et al.

Citations

  1. ↑ 1.0 1.1 Hoyle, F. (1946). "The synthesis of the elements from hydrogen". Monthly Notices of the Royal Astronomical Society 106 (5): 343–383. doi:10.1093/mnras/106.5.343. Bibcode: 1946MNRAS.106..343H. 
  2. ↑ 2.0 2.1 Hoyle, F. (1954). "On Nuclear Reactions Occurring in Very Hot STARS. I. The Synthesis of Elements from Carbon to Nickel". The Astrophysical Journal Supplement Series 1: 121. doi:10.1086/190005. Bibcode: 1954ApJS....1..121H. 
  3. ↑ 3.0 3.1 Burbidge, E. M.; Burbidge, G. R.; Fowler, W.A.; Hoyle, F. (1957). "Synthesis of the Elements in Stars". Reviews of Modern Physics 29 (4): 547–650. doi:10.1103/RevModPhys.29.547. Bibcode: 1957RvMP...29..547B. https://authors.library.caltech.edu/45747/1/BURrmp57.pdf. 
  4. ↑ Suess, H. E.; Urey, H. C. (1956). "Abundances of the Elements". Reviews of Modern Physics 28 (1): 53–74. doi:10.1103/RevModPhys.28.53. Bibcode: 1956RvMP...28...53S. 
  5. ↑ Clayton, D. D. (1968). Principles of Stellar Evolution and Nucleosynthesis. University of Chicago Press. 
  6. ↑ Eddington, A. S. (1920). "The internal constitution of the stars". The Observatory 43 (1341): 341–358. doi:10.1126/science.52.1341.233. PMID 17747682. Bibcode: 1920Obs....43..341E. https://zenodo.org/record/1429642. 
  7. ↑ Eddington, A. S. (1920). "The Internal Constitution of the Stars". Nature 106 (2653): 233–240. doi:10.1038/106014a0. PMID 17747682. Bibcode: 1920Natur.106...14E. https://zenodo.org/record/1429642. 
  8. ↑ Selle, D. (October 2012). "Why the Stars Shine". Guidestar. Houston Astronomical Society. pp. 6–8. http://www.astronomyhouston.org/sites/default/files/guidestar/2012October.pdf. 
  9. ↑ Krane, K. S., Modern Physics (Hoboken, NJ: Wiley, 1983), p. 410.
  10. ↑ Bethe, H. A. (1939). "Energy Production in Stars". Physical Review 55 (5): 434–456. doi:10.1103/PhysRev.55.434. PMID 17835673. Bibcode: 1939PhRv...55..434B. 
  11. ↑ Lang, K. R. (2013). The Life and Death of Stars. Cambridge University Press. p. 167. ISBN 978-1-107-01638-5. .
  12. ↑ Clayton, D. D. (1968). Principles of Stellar Evolution and Nucleosynthesis. University of Chicago Press. p. 365.
  13. ↑ Clayton, D. D. (2007). "History of Science: Hoyle's Equation". Science 318 (5858): 1876–1877. doi:10.1126/science.1151167. PMID 18096793. 
  14. ↑ Cameron, A. G. W. (1957). Stellar Evolution, Nuclear Astrophysics, and Nucleogenesis (Report). Atomic Energy of Canada Limited. Report CRL-41. https://fas.org/sgp/eprint/CRL-41.pdf. 
  15. ↑ Clayton, D. D.; Fowler, W. A.; Hull, T. E.; Zimmerman, B. A. (1961). "Neutron capture chains in heavy element synthesis". Annals of Physics 12 (3): 331–408. doi:10.1016/0003-4916(61)90067-7. Bibcode: 1961AnPhy..12..331C. 
  16. ↑ Seeger, P. A.; Fowler, W. A.; Clayton, D. D. (1965). "Nucleosynthesis of Heavy Elements by Neutron Capture". The Astrophysical Journal Supplement Series 11: 121–126. doi:10.1086/190111. Bibcode: 1965ApJS...11..121S. https://tigerprints.clemson.edu/cgi/viewcontent.cgi?article=1307&context=physastro_pubs. 
  17. ↑ Bodansky, D.; Clayton, D. D.; Fowler, W. A. (1968). "Nucleosynthesis During Silicon Burning". Physical Review Letters 20 (4): 161–164. doi:10.1103/PhysRevLett.20.161. Bibcode: 1968PhRvL..20..161B. https://tigerprints.clemson.edu/cgi/viewcontent.cgi?article=1393&context=physastro_pubs. 
  18. ↑ Bodansky, D.; Clayton, D. D.; Fowler, W. A. (1968). "Nuclear Quasi-Equilibrium during Silicon Burning". The Astrophysical Journal Supplement Series 16: 299. doi:10.1086/190176. Bibcode: 1968ApJS...16..299B. https://tigerprints.clemson.edu/physastro_pubs/312. 
  19. ↑ Clayton, D. D. (1964). "Cosmoradiogenic Chronologies of Nucleosynthesis". The Astrophysical Journal 139: 637. doi:10.1086/147791. Bibcode: 1964ApJ...139..637C. https://tigerprints.clemson.edu/cgi/viewcontent.cgi?article=1305&context=physastro_pubs. 
  20. ↑ 20.0 20.1 Jones, Lauren V. (2009), Stars and galaxies, Greenwood guides to the universe, ABC-CLIO, pp. 65–67, ISBN 978-0-313-34075-8, https://books.google.com/books?id=BuyIHbwsm0sC&pg=PA65 
  21. ↑ Seeds, M. A., Foundations of Astronomy (Belmont, CA: Wadsworth Publishing Company, 1986), p. 245.
  22. ↑ 22.0 22.1 22.2 22.3 Böhm-Vitense, Erika (1992), Introduction to Stellar Astrophysics, 3, Cambridge University Press, pp. 93–100, ISBN 978-0-521-34871-3, https://books.google.com/books?id=msZMEvEpxG8C&pg=PA93 
  23. ↑ Reiners, Ansgar; Basri, Gibor (March 2009). "On the magnetic topology of partially and fully convective stars". Astronomy and Astrophysics 496 (3): 787–790. doi:10.1051/0004-6361:200811450. Bibcode: 2009A&A...496..787R. 
  24. ↑ 24.0 24.1 de Loore, Camiel W. H.; Doom, C. (1992), Structure and evolution of single and binary stars, Astrophysics and space science library, 179, Springer, pp. 200–214, ISBN 978-0-7923-1768-5, https://books.google.com/books?id=LJgNIi0vkeYC&pg=PA200 
  25. ↑ 25.0 25.1 25.2 Jeffrey, C. Simon (2010), Goswami, A.; Reddy, B. E., eds., "Principles and Perspectives in Cosmochemistry", Astrophysics and Space Science Proceedings (Springer) 16: 64–66, doi:10.1007/978-3-642-10352-0, ISBN 978-3-642-10368-1, Bibcode: 2010ASSP...16.....G, https://books.google.com/books?id=gCr9WVH0utwC&pg=PA64 
  26. ↑ Karttunen, Hannu; Oja, Heikki (2007), Fundamental astronomy (5th ed.), Springer, p. 247, ISBN 978-3-540-34143-7 .
  27. ↑ "Neutrinos yield first experimental evidence of catalyzed fusion dominant in many stars" (in en). https://phys.org/news/2020-11-neutrinos-yield-experimental-evidence-catalyzed.html. 
  28. ↑ Choppin, G. R., Liljenzin, J.-O., Rydberg, J., & Ekberg, C., Radiochemistry and Nuclear Chemistry (Cambridge, MA: Academic Press, 2013), p. 357.
  29. ↑ Agostini, M.; Altenmüller, K.; Appel, S.; Atroshchenko, V.; Bagdasarian, Z.; Basilico, D.; Bellini, G.; Benziger, J. et al. (25 November 2020). "Experimental evidence of neutrinos produced in the CNO fusion cycle in the Sun" (in en). Nature 587 (7835): 577–582. doi:10.1038/s41586-020-2934-0. ISSN 1476-4687. PMID 33239797. Bibcode: 2020Natur.587..577B. https://www.nature.com/articles/s41586-020-2934-0. 
  30. ↑ Reid, I. Neill; Hawley, Suzanne L. (2005), New light on dark stars: red dwarfs, low-mass stars, brown dwarfs, Springer-Praxis books in astrophysics and astronomy (2nd ed.), Springer, p. 108, ISBN 978-3-540-25124-8 .
  31. ↑ Salaris, Maurizio; Cassisi, Santi (2005), Evolution of stars and stellar populations, John Wiley and Sons, pp. 119–123, ISBN 978-0-470-09220-0, https://books.google.com/books?id=p4ojTNkcFx8C&pg=PA119 
  32. ↑ Schuler, S. C.; King, J. R.; The, L.-S. (2009), "Stellar Nucleosynthesis in the Hyades Open Cluster", The Astrophysical Journal 701 (1): 837–849, doi:10.1088/0004-637X/701/1/837, Bibcode: 2009ApJ...701..837S 
  33. ↑ Wolf, E. L., Physics and Technology of Sustainable Energy (Oxford, Oxford University Press, 2018), p. 5.
  34. ↑ Karttunen, H., Kröger, P., Oja, H., Poutanen, M., & Donner, K. J., eds., Fundamental Astronomy (Berlin/Heidelberg: Springer, 1987), p. 250.
  35. ↑ Rehder, D., Chemistry in Space: From Interstellar Matter to the Origin of Life (Weinheim: Wiley-VCH, 2010), p. 30.
  36. ↑ Iliadis, C., Nuclear Physics of Stars (Weinheim: Wiley-VCH, 2015), p. 185.
  37. ↑ "University College London astrophysics course: lecture 7 – Stars". http://zuserver2.star.ucl.ac.uk/~idh/PHAS2112/Lectures/Current/Part7.pdf. 
  38. ↑ Maoz, D., Astrophysics in a Nutshell (Princeton: Princeton University Press, 2007), ch. 3.
  39. ↑ Adelberger, Eric G.; Austin, Sam M.; Bahcall, John N.; Balantekin, A. B.; Bogaert, Gilles; Brown, Lowell S.; Buchmann, Lothar; Cecil, F. Edward et al. (1998-10-01). "Solar fusion cross sections" (in en). Reviews of Modern Physics 70 (4): 1265–1291. doi:10.1103/RevModPhys.70.1265. ISSN 0034-6861. Bibcode: 1998RvMP...70.1265A. 
  40. ↑ Adelberger, E. G. (2011). "Solar fusion cross sections. II. Theppchain and CNO cycles". Reviews of Modern Physics 83 (1): 195–245. doi:10.1103/RevModPhys.83.195. Bibcode: 2011RvMP...83..195A. 
  41. ↑ Goupil, M., Belkacem, K., Neiner, C., Lignières, F., & Green, J. J., eds., Studying Stellar Rotation and Convection: Theoretical Background and Seismic Diagnostics (Berlin/Heidelberg: Springer, 2013), p. 211.

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Stellar_nucleosynthesis&oldid=3281083"