Physics:Antiferromagnetism
| Condensed matter physics |
|---|
 |
| Phases · Phase transition · QCP |
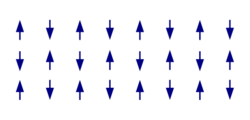
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins (on different sublattices) pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933.[1]
Generally, antiferromagnetic order may exist at sufficiently low temperatures, but vanishes at and above the Néel temperature – named after Louis Néel, who had first identified this type of magnetic ordering.[2] Above the Néel temperature, the material is typically paramagnetic.
Measurement
When no external field is applied, the antiferromagnetic structure corresponds to a vanishing total magnetization. In an external magnetic field, a kind of ferrimagnetic behavior may be displayed in the antiferromagnetic phase, with the absolute value of one of the sublattice magnetizations differing from that of the other sublattice, resulting in a nonzero net magnetization. Although the net magnetization should be zero at a temperature of absolute zero, the effect of spin canting often causes a small net magnetization to develop, as seen for example in hematite.[citation needed]
The magnetic susceptibility of an antiferromagnetic material typically shows a maximum at the Néel temperature. In contrast, at the transition between the ferromagnetic to the paramagnetic phases the susceptibility will diverge. In the antiferromagnetic case, a divergence is observed in the staggered susceptibility.
Various microscopic (exchange) interactions between the magnetic moments or spins may lead to antiferromagnetic structures. In the simplest case, one may consider an Ising model on a bipartite lattice, e.g. the simple cubic lattice, with couplings between spins at nearest neighbor sites. Depending on the sign of that interaction, ferromagnetic or antiferromagnetic order will result. Geometrical frustration or competing ferro- and antiferromagnetic interactions may lead to different and, perhaps, more complicated magnetic structures.
The relationship between magnetization and the magnetizing field is non-linear like in ferromagnetic materials. This fact is due to the contribution of the hysteresis loop,[3] which for ferromagnetic materials involves a residual magnetization.
Antiferromagnetic materials
Antiferromagnetic structures were first shown through neutron diffraction of transition metal oxides such as nickel, iron, and manganese oxides. The experiments, performed by Clifford Shull, gave the first results showing that magnetic dipoles could be oriented in an antiferromagnetic structure.[4]
Antiferromagnetic materials occur commonly among transition metal compounds, especially oxides. Examples include hematite, metals such as chromium, alloys such as iron manganese (FeMn), and oxides such as nickel oxide (NiO). There are also numerous examples among high nuclearity metal clusters. Organic molecules can also exhibit antiferromagnetic coupling under rare circumstances, as seen in radicals such as 5-dehydro-m-xylylene.
Antiferromagnets can couple to ferromagnets, for instance, through a mechanism known as exchange bias, in which the ferromagnetic film is either grown upon the antiferromagnet or annealed in an aligning magnetic field, causing the surface atoms of the ferromagnet to align with the surface atoms of the antiferromagnet. This provides the ability to "pin" the orientation of a ferromagnetic film, which provides one of the main uses in so-called spin valves, which are the basis of magnetic sensors including modern hard disk drive read heads. The temperature at or above which an antiferromagnetic layer loses its ability to "pin" the magnetization direction of an adjacent ferromagnetic layer is called the blocking temperature of that layer and is usually lower than the Néel temperature.
Geometric frustration
Unlike ferromagnetism, anti-ferromagnetic interactions can lead to multiple optimal states (ground states—states of minimal energy). In one dimension, the anti-ferromagnetic ground state is an alternating series of spins: up, down, up, down, etc. Yet in two dimensions, multiple ground states can occur.
Consider an equilateral triangle with three spins, one on each vertex. If each spin can take on only two values (up or down), there are 23 = 8 possible states of the system, six of which are ground states. The two situations which are not ground states are when all three spins are up or are all down. In any of the other six states, there will be two favorable interactions and one unfavorable one. This illustrates frustration: the inability of the system to find a single ground state. This type of magnetic behavior has been found in minerals that have a crystal stacking structure such as a Kagome lattice or hexagonal lattice.
Other properties
Synthetic antiferromagnets (often abbreviated by SAF) are artificial antiferromagnets consisting of two or more thin ferromagnetic layers separated by a nonmagnetic layer.[5] Dipole coupling of the ferromagnetic layers results in antiparallel alignment of the magnetization of the ferromagnets.
Antiferromagnetism plays a crucial role in giant magnetoresistance, as had been discovered in 1988 by the Nobel prize winners Albert Fert and Peter Grünberg (awarded in 2007) using synthetic antiferromagnets.
There are also examples of disordered materials (such as iron phosphate glasses) that become antiferromagnetic below their Néel temperature. These disordered networks 'frustrate' the antiparallelism of adjacent spins; i.e. it is not possible to construct a network where each spin is surrounded by opposite neighbour spins. It can only be determined that the average correlation of neighbour spins is antiferromagnetic. This type of magnetism is sometimes called speromagnetism.
See also
- Physics:Exchange bias
- Physics:Giant magnetoresistance – Phenomenom involving the change of conductivity in metallic layers
- Physics:Ising model – Mathematical model of ferromagnetism in statistical mechanics
- Physics:ANNNI model – Variant of the Ising model
- Physics:Quantum spin liquid – Phase of matter
- Physics:Ferromagnetism – Mechanism by which materials form into and are attracted to magnets
- Physics:Diamagnetism – Magnetic property of ordinary materials
References
- ↑ Landau, L. D. (1933). A possible explanation of the field dependence of the susceptibility at low temperatures. Phys. Z. Sowjet, 4, 675.
- ↑ M. Louis Néel (1948). "Propriétées magnétiques des ferrites; Férrimagnétisme et antiferromagnétisme". Annales de Physique 12 (3): 137–198. doi:10.1051/anphys/194812030137. Bibcode: 1948AnPh...12..137N. https://hal.archives-ouvertes.fr/hal-02888371/file/N%C3%A9el%20-%201948%20-%20Propri%C3%A9t%C3%A9s%20magn%C3%A9tiques%20des%20ferrites%20%3B%20ferrimagn%C3%A9ti.pdf.
- ↑ František, Hrouda (September 1, 2002). "Low-field variation of magnetic susceptibility and its effect on the anisotropy of magnetic susceptibility of rocks". Geophysical Journal International (Oxford University Press) 150 (3): 715–723. doi:10.1046/j.1365-246X.2002.01731.x. ISSN 1365-246X. OCLC 198890763. Bibcode: 2002GeoJI.150..715H.
- ↑ Shull, C. G.; Strauser, W. A.; Wollan, E. O. (1951-07-15). "Neutron Diffraction by Paramagnetic and Antiferromagnetic Substances". Physical Review (American Physical Society (APS)) 83 (2): 333–345. doi:10.1103/physrev.83.333. ISSN 0031-899X. Bibcode: 1951PhRv...83..333S.
- ↑ M. Forrester and F. Kusmartsev (2014). "The nano-mechanics and magnetic properties of high moment synthetic antiferromagnetic particles". Physica Status Solidi A 211 (4): 884–889. doi:10.1002/pssa.201330122. Bibcode: 2014PSSAR.211..884F. https://dspace.lboro.ac.uk/2134/16577.
External links
- Magnetism: Models and Mechanisms in E. Pavarini, E. Koch, and U. Schollwöck: Emergent Phenomena in Correlated Matter, Jülich 2013, ISBN:978-3-89336-884-6
 |