Physics:Time crystal

From HandWiki
Short description: Structure that repeats in time; a novel type or phase of non-equilibrium matter
Condensed matter physics
QuantumPhaseTransition.svg
Phases · Phase transition · QCP
States of matter
Solid · Liquid · Gas · Plasma · Bose–Einstein condensate · Bose gas · Fermionic condensate · Fermi gas · Fermi liquid · Supersolid · Superfluidity · Luttinger liquid  · Time crystal

In condensed matter physics, a time crystal is a quantum system of particles whose lowest-energy state is one in which the particles are in repetitive motion. The system cannot lose energy to the environment and come to rest because it is already in its quantum ground state. Because of this, the motion of the particles does not really represent kinetic energy like other motion; it has "motion without energy". Time crystals were first proposed theoretically by Frank Wilczek in 2012 as a time-based analogue to common crystals – whereas the atoms in crystals are arranged periodically in space, the atoms in a time crystal are arranged periodically in both space and time.[1] Several different groups have demonstrated matter with stable periodic evolution in systems that are periodically driven.[2][3][4][5] In terms of practical use, time crystals may one day be used as quantum computer memory.[6]

The existence of crystals in nature is a manifestation of spontaneous symmetry breaking, which occurs when the lowest-energy state of a system is less symmetrical than the equations governing the system. In the crystal ground state, the continuous translational symmetry in space is broken and replaced by the lower discrete symmetry of the periodic crystal. As the laws of physics are symmetrical under continuous translations in time as well as space, the question arose in 2012 as to whether it is possible to break symmetry temporally, and thus create a "time crystal" that is resistant to entropy.[1]

If a discrete time translation symmetry is broken (which may be realized in periodically driven systems), then the system is referred to as a discrete time crystal. A discrete time crystal never reaches thermal equilibrium, as it is a type (or phase) of non-equilibrium matter. Breaking of time symmetry can only occur in non-equilibrium systems.[5] Discrete time crystals have in fact been observed in physics laboratories as early as 2016 (published in 2017). One example of a time crystal, which demonstrates non-equilibrium, broken time symmetry is a constantly rotating ring of charged ions in an otherwise lowest-energy state.[6]

Concept

Ordinary (non-time) crystals form through spontaneous symmetry breaking related to a spatial symmetry. Such processes can produce materials with interesting properties, such as diamonds, salt crystals, and ferromagnetic metals. By analogy, a time crystal arises through the spontaneous breaking of a time translation symmetry. A time crystal can be informally defined as a time-periodic self-organizing structure. While an ordinary crystal is periodic (has a repeating structure) in space, a time crystal has a repeating structure in time. A time crystal is periodic in time in the same sense that the pendulum in a pendulum-driven clock is periodic in time. Unlike a pendulum, a time crystal "spontaneously" self-organizes into robust periodic motion (breaking a temporal symmetry).[7]

Time translation symmetry

Main page: Physics:Time translation symmetry

Symmetries in nature lead directly to conservation laws, something which is precisely formulated by the Noether theorem.[8]

The basic idea of time-translation symmetry is that a translation in time has no effect on physical laws, i.e. that the laws of nature that apply today were the same in the past and will be the same in the future.[9] This symmetry implies the conservation of energy.[10]

Broken symmetry in normal crystals

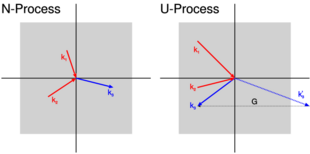
Normal process (N-process) and Umklapp process (U-process). While the N-process conserves total phonon momentum, the U-process changes phonon momentum.

Common crystals exhibit broken translation symmetry: they have repeated patterns in space and are not invariant under arbitrary translations or rotations. The laws of physics are unchanged by arbitrary translations and rotations. However, if we hold fixed the atoms of a crystal, the dynamics of an electron or other particle in the crystal depend on how it moves relative to the crystal, and particle momentum can change by interacting with the atoms of a crystal — for example in Umklapp processes.[11] Quasimomentum, however, is conserved in a perfect crystal.[12]

Time crystals show a broken symmetry analogous to a discrete space-translation symmetry breaking. For example,[citation needed] the molecules of a liquid freezing on the surface of a crystal can align with the molecules of the crystal, but with a pattern less symmetric than the crystal: it breaks the initial symmetry. This broken symmetry exhibits three important characteristics:[citation needed]

  • the system has a lower symmetry than the underlying arrangement of the crystal,
  • the system exhibits spatial and temporal long-range order (unlike a local and intermittent order in a liquid near the surface of a crystal),
  • it is the result of interactions between the constituents of the system, which align themselves relative to each other.

Broken symmetry in discrete time crystals (DTC)

Time crystals seem to break time-translation symmetry and have repeated patterns in time even if the laws of the system are invariant by translation of time. The time crystals that are experimentally realized show discrete time-translation symmetry breaking, not the continuous one: they are periodically driven systems oscillating at a fraction of the frequency of the driving force. (According to Philip Ball, DTC are so-called because "their periodicity is a discrete, integer multiple of the driving period".[13])

The initial symmetry, which is the discrete time-translation symmetry ([math]\displaystyle{ t \to t + nT }[/math]) with [math]\displaystyle{ n=1 }[/math], is spontaneously broken to the lower discrete time-translation symmetry with [math]\displaystyle{ n\gt 1 }[/math], where [math]\displaystyle{ t }[/math] is time, [math]\displaystyle{ T }[/math] the driving period, [math]\displaystyle{ n }[/math] an integer.[14]

Many systems can show behaviors of spontaneous time translation symmetry breaking but may not be discrete (or Floquet) time crystals: convection cells, oscillating chemical reactions, aerodynamic flutter, and subharmonic response to a periodic driving force such as the Faraday instability, NMR spin echos, parametric down-conversion, and period-doubled nonlinear dynamical systems.[14]

However, discrete (or Floquet) time crystals are unique in that they follow a strict definition of discrete time-translation symmetry breaking:[15]

  • it is a broken symmetry – the system shows oscillations with a period longer than the driving force,
  • the system is in crypto-equilibrium – these oscillations generate no entropy, and a time-dependent frame can be found in which the system is indistinguishable from an equilibrium when measured stroboscopically[15] (which is not the case of convection cells, oscillating chemical reactions and aerodynamic flutter),
  • the system exhibits long-range order – the oscillations are in phase (synchronized) over arbitrarily long distances and time.

Moreover, the broken symmetry in time crystals is the result of many-body interactions: the order is the consequence of a collective process, just like in spatial crystals.[14] This is not the case for NMR spin echos.

These characteristics makes discrete time crystals analogous to spatial crystals as described above and may be considered a novel type or phase of nonequilibrium matter.[14]

Thermodynamics

Time crystals do not violate the laws of thermodynamics: energy in the overall system is conserved, such a crystal does not spontaneously convert thermal energy into mechanical work, and it cannot serve as a perpetual store of work. But it may change perpetually in a fixed pattern in time for as long as the system can be maintained. They possess "motion without energy"[16]—their apparent motion does not represent conventional kinetic energy.[17] Recent experimental advances in probing discrete time crystals in their periodically driven nonequilibrium states have led to the beginning exploration of novel phases of nonequilibrium matter.[14]

Time crystals do not evade the Second Law of Thermodynamics,[18] although they are the first objects to spontaneously break "time-translation symmetry", the usual rule that a stable object will remain the same throughout time. In thermodynamics, a time crystal's entropy, understood as a measure of disorder in the system, remains stationary over time, marginally satisfying the second law of thermodynamics by not decreasing.[19][20]

History

Nobel laureate Frank Wilczek at University of Paris-Saclay

The idea of a quantized time crystal was theorized in 2012 by Frank Wilczek,[21][22] a Nobel laureate and professor at MIT. In 2013, Xiang Zhang, a nanoengineer at University of California, Berkeley, and his team proposed creating a time crystal in the form of a constantly rotating ring of charged ions.[23][24]

In response to Wilczek and Zhang, Patrick Bruno (European Synchrotron Radiation Facility) and Masaki Oshikawa (University of Tokyo) published several articles stating that space–time crystals were impossible.[25][26]

Subsequent work developed more precise definitions of time translation symmetry-breaking, which ultimately led to the Watanabe–Oshikawa "no-go" statement that quantum space–time crystals in equilibrium are not possible.[27][28] Later work restricted the scope of Watanabe and Oshikawa: strictly speaking, they showed that long-range order in both space and time is not possible in equilibrium, but breaking of time translation symmetry alone is still possible.[29][30][31]

Several realizations of time crystals, which avoid the equilibrium no-go arguments, were later proposed.[32] In 2014 Krzysztof Sacha (pl) at Jagiellonian University in Krakow predicted the behaviour of discrete time crystals in a periodically driven system with "an ultracold atomic cloud bouncing on an oscillating mirror".[33][34]

In 2016, research groups at Princeton and at Santa Barbara independently suggested that periodically driven quantum spin systems could show similar behaviour.[35] Also in 2016, Norman Yao at Berkeley and colleagues proposed a different way to create discrete time crystals in spin systems.[36] These ideas were successful and independently realized by two experimental teams: a group led by Harvard's Mikhail Lukin[37] and a group led by Christopher Monroe at University of Maryland.[38] Both experiments were published in the same issue of Nature in March 2017.

Later, time crystals in open systems, so called dissipative time crystals, were proposed in several platforms breaking a discrete [39][40][41][42] and a continuous[43][44] time-translation symmetry. A dissipative time crystal was experimentally realized for the first time in 2021 by the group of Andreas Hemmerich at the Institute of Laser Physics at the University of Hamburg.[45] The researchers used a Bose–Einstein condensate strongly coupled to a dissipative optical cavity and the time crystal was demonstrated to spontaneously break discrete time translation symmetry by periodically switching between two atomic density patterns.[45][46][47] In an earlier experiment in the group of Tilman Esslinger at ETH Zurich, limit cycle dynamics[48] was observed in 2019,[49] but evidence of robustness against perturbations and the spontaneous character of the time translation symmetry breaking were not addressed.

In 2019 physicists Valerii Kozin and Oleksandr Kyriienko proved that, in theory, a permanent quantum time crystal can exist as an isolated system if the system contains unusual long-range multiparticle interactions. The original "no-go" argument only holds in the presence of typical short-range fields that decay as quickly as r−α for some α > 0. Kozin and Kyriienko instead analyzed a spin-1/2 many-body Hamiltonian with long-range multispin interactions, and showed it broke continuous time-translational symmetry. Certain spin correlations in the system oscillate in time, despite the system being closed and in a ground energy state. However, demonstrating such a system in practice might be prohibitively difficult,[50][51] and concerns about the physicality of the long-range nature of the model have been raised.[52]

In 2022, the Hamburg research team, supervised by Hans Keßler and Andreas Hemmerich, demonstrated, for the first time, a continuous dissipative time crystal exhibiting spontaneous breaking of continuous time-translation symmetry.[53][54][55][56]

Experiments

In October 2016, Christopher Monroe at the University of Maryland claimed to have created the world's first discrete time crystal. Using the ideas proposed by Yao et al.,[36] his team trapped a chain of 171Yb+ ions in a Paul trap, confined by radio-frequency electromagnetic fields. One of the two spin states was selected by a pair of laser beams. The lasers were pulsed, with the shape of the pulse controlled by an acousto-optic modulator, using the Tukey window to avoid too much energy at the wrong optical frequency. The hyperfine electron states in that setup, 2S1/2 |F = 0, mF = 0⟩ and |F = 1, mF = 0⟩, have very close energy levels, separated by 12.642831 GHz. Ten Doppler-cooled ions were placed in a line 0.025 mm long and coupled together.

The researchers observed a subharmonic oscillation of the drive. The experiment showed "rigidity" of the time crystal, where the oscillation frequency remained unchanged even when the time crystal was perturbed, and that it gained a frequency of its own and vibrated according to it (rather than only the frequency of the drive). However, once the perturbation or frequency of vibration grew too strong, the time crystal "melted" and lost this subharmonic oscillation, and it returned to the same state as before where it moved only with the induced frequency.[38]

Also in 2016, Mikhail Lukin at Harvard also reported the creation of a driven time crystal. His group used a diamond crystal doped with a high concentration of nitrogen-vacancy centers, which have strong dipole–dipole coupling and relatively long-lived spin coherence. This strongly interacting dipolar spin system was driven with microwave fields, and the ensemble spin state was determined with an optical (laser) field. It was observed that the spin polarization evolved at half the frequency of the microwave drive. The oscillations persisted for over 100 cycles. This subharmonic response to the drive frequency is seen as a signature of time-crystalline order.[37]

In May 2018, a group in Aalto University reported that they had observed the formation of a time quasicrystal and its phase transition to a continuous time crystal in a Helium-3 superfluid cooled to within one ten thousandth of a kelvin from absolute zero (0.0001 K). [57] On August 17, 2020 Nature Materials published a letter from the same group saying that for the first time they were able to observe interactions and the flow of constituent particles between two time crystals. [58]

In February 2021 a team at Max Planck Institute for Intelligent Systems described the creation of time crystal consisting of magnons and probed them under scanning transmission X-ray microscopy to capture the recurring periodic magnetization structure in the first known video record of such type.[59][60]

In July 2021, a team led by Andreas Hemmerich at the Institute of Laser Physics at the University of Hamburg presented the first realization of a time crystal in an open system, a so-called dissipative time crystal using ultracold atoms coupled to an optical cavity. The main achievement of this work is a positive application of dissipation – actually helping to stabilise the system's dynamics.[45][46][47]

In November 2021 a collaboration between Google and physicists from multiple universities reported the observation of a discrete time crystal on Google's Sycamore processor, a quantum computing device. A chip of 20 qubits was used to obtain a many-body localization configuration of up and down spins and then stimulated with a laser to achieve a periodically driven "Floquet" system where all up spins are flipped for down and vice-versa in periodic cycles which are multiples of the laser's frequency. While the laser is necessary to maintain the necessary environmental conditions, no energy is absorbed from the laser, so the system remains in a protected eigenstate order.[20][61]

Previously in June and November 2021 other teams had obtained virtual time crystals based on floquet systems under similar principles to those of the Google experiment, but on quantum simulators rather than quantum processors: first a group at the University of Maryland obtained time crystals on trapped-ions qubits using high frequency driving rather than many-body localization[62][63] and then a collaboration between TU Delft and TNO in the Netherlands called Qutech created time crystals from nuclear spins in carbon-13 nitrogen-vacancy (NV) centers on a diamond, attaining longer times but fewer qubits.[64][65]

In February 2022 a scientist at UC Riverside reported a dissipative time crystal akin to the system of July 2021 but all-optical, which allowed the scientist to operate it at room temperature. In this experiment injection locking was used to direct lasers at a specific frequency inside a microresonator creating a lattice trap for solitons at subharmonic frequencies.[66][67]

In March 2022 a new experiment studying time crystals on a quantum processor was performed by two physicists at the university of Melbourne, this time using IBM's Manhattan and Brooklyn quantum processors observing a total of 57 qubits.[68][69][70]

In June 2022 the observation of a continuous time crystal was reported by a team at the Institute of Laser Physics at the University of Hamburg, supervised by Hans Keßler and Andreas Hemmerich. In periodically driven systems, time translation symmetry is broken into a discrete time-translation symmetry due to the drive. Discrete time crystals break this discrete time-translation symmetry by oscillating at a multiple of the drive frequency. In the new experiment, the drive (pump laser) was operated continuously, thus respecting the continuous time translation symmetry. Instead of a subharmonic response, the system showed an oscillation with an intrinsic frequency and a time phase taking random values between 0 and 2π, as expected for spontaneous breaking of continuous time translation symmetry. Moreover, the observed limit cycle oscillations were shown to be robust against perturbations of technical or fundamental character, such as quantum noise and, due to the openness of the system, fluctuations associated with dissipation. The system consisted of a Bose–Einstein condensate in an optical cavity, which was pumped with an optical standing wave oriented perpendicularly with regard to the cavity axis and was in a superradiant phase localizing at two bistable ground states between which it oscillated.[53][54][55][56]


References

  1. ↑ 1.0 1.1 Zakrzewski, Jakub (15 October 2012). "Viewpoint: Crystals of Time". APS Physics. http://physics.aps.org/articles/v5/116. 
  2. ↑ Sacha, Krzysztof (2015). "Modeling spontaneous breaking of time-translation symmetry". Physical Review A 91 (3): 033617. doi:10.1103/PhysRevA.91.033617. ISSN 1050-2947. Bibcode: 2015PhRvA..91c3617S. 
  3. ↑ Khemani et al. (2016)
  4. ↑ Else et al. (2016).
  5. ↑ 5.0 5.1 Richerme, Phil (January 18, 2017). "How to Create a Time Crystal". Physics (American Physical Society) 10: 5. doi:10.1103/Physics.10.5. Bibcode: 2017PhyOJ..10....5R. https://physics.aps.org/articles/v10/5. Retrieved 5 April 2021. 
  6. ↑ 6.0 6.1 "Physicists Create World's First Time Crystal". https://www.technologyreview.com/2016/10/04/157185/physicists-create-worlds-first-time-crystal/. 
  7. ↑ Sacha, Krzysztof; Zakrzewski, Jakub (1 January 2018). "Time crystals: a review". Reports on Progress in Physics 81 (1): 016401. doi:10.1088/1361-6633/aa8b38. PMID 28885193. Bibcode: 2018RPPh...81a6401S. 
  8. ↑ Cao, Tian Yu (25 March 2004). Conceptual Foundations of Quantum Field Theory. Cambridge: Cambridge University Press. ISBN 978-0-521-60272-3. https://books.google.com/books?id=d0wS0EJHZ3MC.  See p. 151.
  9. ↑ Wilczek, Frank (16 July 2015). A Beautiful Question: Finding Nature's Deep Design. Penguin Books Limited. ISBN 978-1-84614-702-9. https://books.google.com/books?id=Oh3ICAAAQBAJ.  See Ch. 3.
  10. ↑ Feng, Duan; Jin, Guojun (2005). Introduction to Condensed Matter Physics. singapore: World Scientific. ISBN 978-981-238-711-0. https://books.google.com/books?id=-iuYN5arHwoC.  See p. 18.
  11. ↑ Sólyom, Jenö (19 September 2007). Fundamentals of the Physics of Solids: Volume 1: Structure and Dynamics. Springer. ISBN 978-3-540-72600-5. https://books.google.com/books?id=zn-se2TKv3QC.  See p. 193.
  12. ↑ Sólyom, Jenö (19 September 2007). Fundamentals of the Physics of Solids: Volume 1: Structure and Dynamics. Springer. ISBN 978-3-540-72600-5. https://books.google.com/books?id=zn-se2TKv3QC.  See p. 191.
  13. ↑ Ball, Philip (July 17, 2018). "In search of time crystals". Physics World 31 (7): 29. doi:10.1088/2058-7058/31/7/32. Bibcode: 2018PhyW...31g..29B. https://physicsworld.com/a/in-search-of-time-crystals/. Retrieved September 6, 2021. "The “discrete” comes from the fact that their periodicity is a discrete, integer multiple of the driving period.". 
  14. ↑ 14.0 14.1 14.2 14.3 14.4 Else, D. W.; Monroe, C.; Nayak, C.; Yao, N. Y. (March 2020). "Discrete Time Crystals". Annual Review of Condensed Matter Physics 11: 467–499. doi:10.1146/annurev-conmatphys-031119-050658. Bibcode: 2020ARCMP..11..467E. https://doi.org/10.1146/annurev-conmatphys-031119-050658. 
  15. ↑ 15.0 15.1 Yao; Nayak (2018). "Time crystals in periodically driven systems". Physics Today 71 (9): 40–47. doi:10.1063/PT.3.4020. ISSN 0031-9228. Bibcode: 2018PhT....71i..40Y. 
  16. ↑ Crew, Bec. "Time Crystals Might Exist After All – And They Could Break Space-Time Symmetry" (in en-gb). ScienceAlert. https://www.sciencealert.com/time-crystals-might-exist-after-all-and-they-could-break-the-symmetry-of-space-and-time. 
  17. ↑ Cowen, Ron (2017-02-02). "'Time Crystals' Could Be a Legitimate Form of Perpetual Motion". Scientific American. https://www.scientificamerican.com/article/time-crystals-could-be-legitimate-form-perpetual-motion/. 
  18. ↑ "Google May Have Created an Unruly New State of Matter: Time Crystals". Popular Mechanics. https://www.popularmechanics.com/science/a37211606/google-time-crystal-quantum-computing/. 
  19. ↑ Kubota, Taylor; University, Stanford. "Physicists create time crystals with quantum computers" (in en). https://phys.org/news/2021-11-physicists-crystals-quantum.html. 
  20. ↑ 20.0 20.1 Mi, Xiao; Ippoliti, Matteo; Quintana, Chris; Greene, Ami; Chen, Zijun; Gross, Jonathan; Arute, Frank; Arya, Kunal et al. (2022). "Time-Crystalline Eigenstate Order on a Quantum Processor" (in en). Nature 601 (7894): 531–536. doi:10.1038/s41586-021-04257-w. ISSN 1476-4687. PMID 34847568. Bibcode: 2022Natur.601..531M. 
  21. ↑ Wilczek, Frank (2012). "Quantum Time Crystals". Physical Review Letters 109 (16): 160401. doi:10.1103/PhysRevLett.109.160401. ISSN 0031-9007. PMID 23215056. Bibcode: 2012PhRvL.109p0401W. 
  22. ↑ Shapere, Alfred; Wilczek, Frank (2012). "Classical Time Crystals". Physical Review Letters 109 (16): 160402. doi:10.1103/PhysRevLett.109.160402. ISSN 0031-9007. PMID 23215057. Bibcode: 2012PhRvL.109p0402S. 
  23. ↑ See Li et al. (2012a, 2012b).
  24. ↑ Wolchover, Natalie (25 April 2013). "Perpetual Motion Test Could Amend Theory of Time". Simons Foundation. https://www.quantamagazine.org/20130425-perpetual-motion-test-could-amend-theory-of-time/#. 
  25. ↑ See Bruno (2013a) and Bruno (2013b).
  26. ↑ Thomas, Jessica (15 March 2013). "Notes from the Editors: The Aftermath of a Controversial Idea". APS Physics. http://physics.aps.org/articles/v6/31. 
  27. ↑ See Nozières (2013), Yao et al. (2017), p. 1 and Volovik (2013).
  28. ↑ Watanabe, Haruki; Oshikawa, Masaki (2015). "Absence of Quantum Time Crystals". Physical Review Letters 114 (25): 251603. doi:10.1103/PhysRevLett.114.251603. ISSN 0031-9007. PMID 26197119. Bibcode: 2015PhRvL.114y1603W. 
  29. ↑ Medenjak, Marko; Buča, Berislav; Jaksch, Dieter (2020-07-20). "Isolated Heisenberg magnet as a quantum time crystal". Physical Review B 102 (4): 041117. doi:10.1103/physrevb.102.041117. ISSN 2469-9950. Bibcode: 2020PhRvB.102d1117M. 
  30. ↑ Khemani, Vedika; Moessner, Roderich; Sondhi, S. L. (23 October 2019). "A Brief History of Time Crystals". arXiv:1910.10745 [cond-mat.str-el].
  31. ↑ Uhrich, P.; Defenu, N.; Jafari, R.; Halimeh, J. C. (2020). "Out-of-equilibrium phase diagram of long-range superconductors". Physical Review B 101 (24): 245148. doi:10.1103/physrevb.101.245148. Bibcode: 2020PhRvB.101x5148U. 
  32. ↑ See Wilczek (2013b) and Yoshii et al. (2015).
  33. ↑ Sacha, Krzysztof (2015). "Modeling spontaneous breaking of time-translation symmetry". Physical Review A 91 (3): 033617. doi:10.1103/PhysRevA.91.033617. ISSN 1050-2947. Bibcode: 2015PhRvA..91c3617S. "We show that an ultracold atomic cloud bouncing on an oscillating mirror can reveal spontaneous breaking of a discrete time-translation symmetry". 
  34. ↑ Sacha, Krzysztof (2020). Time Crystals. Springer Series on Atomic, Optical, and Plasma Physics. 114. Springer. doi:10.1007/978-3-030-52523-1. ISBN 978-3-030-52522-4. https://link.springer.com/book/10.1007%2F978-3-030-52523-1. 
  35. ↑ See Khemani et al. (2016) and Else et al. (2016)
  36. ↑ 36.0 36.1 Yao, N. Y.; Potter, A. C.; Potirniche, I.-D.; Vishwanath, A. (2017). "Discrete Time Crystals: Rigidity, Criticality, and Realizations". Physical Review Letters 118 (3): 030401. doi:10.1103/PhysRevLett.118.030401. ISSN 0031-9007. PMID 28157355. Bibcode: 2017PhRvL.118c0401Y. https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.118.030401. 
  37. ↑ 37.0 37.1 Choi, Soonwon; Choi, Joonhee; Landig, Renate; Kucsko, Georg; Zhou, Hengyun; Isoya, Junichi; Jelezko, Fedor; Onoda, Shinobu et al. (2017). "Observation of discrete time-crystalline order in a disordered dipolar many-body system". Nature 543 (7644): 221–225. doi:10.1038/nature21426. ISSN 0028-0836. PMID 28277511. Bibcode: 2017Natur.543..221C. 
  38. ↑ 38.0 38.1 Zhang, J.; Hess, P. W.; Kyprianidis, A.; Becker, P.; Lee, A.; Smith, J.; Pagano, G.; Potirniche, I.-D. et al. (2017). "Observation of a discrete time crystal". Nature 543 (7644): 217–220. doi:10.1038/nature21413. PMID 28277505. Bibcode: 2017Natur.543..217Z. 
  39. ↑ Iemini, Fernando; Russomanno, Angelo; Keeling, Jonathan; Schirò, Marco; Dalmonte, Marcello; Fazio, Rosario (16 July 2018). "Boundary time crystals". Phys. Rev. Lett. 121 (35301): 035301. doi:10.1103/PhysRevLett.121.035301. PMID 30085780. Bibcode: 2018PhRvL.121c5301I. 
  40. ↑ Gong, Zongping; Hamazaki, Ryusuke; Ueda, Masahito (25 January 2018). "Discrete Time-Crystalline Order in Cavity and Circuit QED Systems". Phys. Rev. Lett. 120 (40404): 040404. doi:10.1103/PhysRevLett.120.040404. PMID 29437420. Bibcode: 2018PhRvL.120d0404G. 
  41. ↑ Filippo Maria, Gambetta; Carollo, Federico; Marcuzzi, Matteo; Garrahan, Juan P.; Lesanovsky, Igor (8 January 2019). "Discrete Time Crystals in the Absence of Manifest Symmetries or Disorder in Open Quantum Systems". Phys. Rev. Lett. 122 (15701): 015701. doi:10.1103/PhysRevLett.122.015701. PMID 31012672. Bibcode: 2019PhRvL.122a5701G. 
  42. ↑ Buča, Berislav; Jaksch, Dieter (2019-12-23). "Dissipation Induced Nonstationarity in a Quantum Gas". Physical Review Letters 123 (26): 260401. doi:10.1103/PhysRevLett.123.260401. PMID 31951440. Bibcode: 2019PhRvL.123z0401B. https://link.aps.org/doi/10.1103/PhysRevLett.123.260401. 
  43. ↑ Iemini, F.; Russomanno, A.; Keeling, J.; Schirò, M.; Dalmonte, M.; Fazio, R. (2018-07-16). "Boundary Time Crystals". Physical Review Letters 121 (3): 035301. doi:10.1103/PhysRevLett.121.035301. PMID 30085780. Bibcode: 2018PhRvL.121c5301I. https://link.aps.org/doi/10.1103/PhysRevLett.121.035301. 
  44. ↑ Buča, Berislav; Tindall, Joseph; Jaksch, Dieter (2019-04-15). "Non-stationary coherent quantum many-body dynamics through dissipation". Nature Communications 10 (1): 1730. doi:10.1038/s41467-019-09757-y. ISSN 2041-1723. PMID 30988312. Bibcode: 2019NatCo..10.1730B. 
  45. ↑ 45.0 45.1 45.2 Keßler, Hans; Kongkhambut, Phatthamon; Georges, Christoph; Mathey, Ludwig; Cosme, Jayson G.; Hemmerich, Andreas (2021-07-19). "Observation of a Dissipative Time Crystal". Physical Review Letters 127 (4): 043602. doi:10.1103/PhysRevLett.127.043602. PMID 34355967. Bibcode: 2021PhRvL.127d3602K. https://link.aps.org/doi/10.1103/PhysRevLett.127.043602. 
  46. ↑ 46.0 46.1 Gong, Zongping; Ueda, Masahito (2021-07-19). "Time Crystals in Open Systems" (in en). Physics 14: 104. doi:10.1103/Physics.14.104. Bibcode: 2021PhyOJ..14..104G. https://physics.aps.org/articles/v14/104. 
  47. ↑ 47.0 47.1 Ball, Philip (September 2021). "Quantum time crystals open up" (in en). Nature Materials 20 (9): 1172. doi:10.1038/s41563-021-01090-4. ISSN 1476-4660. PMID 34433935. Bibcode: 2021NatMa..20.1172B. https://www.nature.com/articles/s41563-021-01090-4. 
  48. ↑ Piazza, Francesco; Ritsch, Helmut (2015-10-15). "Self-Ordered Limit Cycles, Chaos, and Phase Slippage with a Superfluid inside an Optical Resonator". Physical Review Letters 115 (16): 163601. doi:10.1103/PhysRevLett.115.163601. PMID 26550874. Bibcode: 2015PhRvL.115p3601P. https://link.aps.org/doi/10.1103/PhysRevLett.115.163601. 
  49. ↑ Dogra, Nishant; Landini, Manuele; Kroeger, Katrin; Hruby, Lorenz; Donner, Tobias; Esslinger, Tilman (2019-12-20). "Dissipation-induced structural instability and chiral dynamics in a quantum gas" (in en). Science 366 (6472): 1496–1499. doi:10.1126/science.aaw4465. ISSN 0036-8075. PMID 31857481. Bibcode: 2019Sci...366.1496D. https://www.science.org/doi/10.1126/science.aaw4465. 
  50. ↑ Cho, Adrian (27 November 2019). "Back to the future: The original time crystal makes a comeback". Science. doi:10.1126/science.aba3793. https://www.science.org/content/article/back-future-original-time-crystal-makes-comeback. 
  51. ↑ Kozin, Valerii K.; Kyriienko, Oleksandr (2019-11-20). "Quantum Time Crystals from Hamiltonians with Long-Range Interactions" (in en). Physical Review Letters 123 (21): 210602. doi:10.1103/PhysRevLett.123.210602. ISSN 0031-9007. PMID 31809146. Bibcode: 2019PhRvL.123u0602K. 
  52. ↑ Khemani, Vedika; Moessner, Roderich; Sondhi, S. L. (2020). "Comment on 'Quantum Time Crystals from Hamiltonians with Long-Range Interactions'". arXiv:2001.11037 [cond-mat.str-el].
  53. ↑ 53.0 53.1 Kongkhambut, Phatthamon; Skulte, Jim; Mathey, Ludwig; Cosme, Jayson G.; Hemmerich, Andreas; Keßler, Hans (2022-08-05). "Observation of a continuous time crystal" (in en). Science 377 (6606): 670–673. doi:10.1126/science.abo3382. ISSN 0036-8075. PMID 35679353. Bibcode: 2022Sci...377..670K. https://www.science.org/doi/10.1126/science.abo3382. 
  54. ↑ 54.0 54.1 LeBlanc, Lindsay J. (2022-08-05). "Unleashing spontaneity in a time crystal" (in en). Science 377 (6606): 576–577. doi:10.1126/science.add2015. ISSN 0036-8075. PMID 35926056. Bibcode: 2022Sci...377..576L. https://www.science.org/doi/10.1126/science.add2015. 
  55. ↑ 55.0 55.1 "Researchers observe continuous time crystal" (in en). https://www.cui-advanced.uni-hamburg.de/en/research/wissenschaftsnews/22-06-10-crystal.html. 
  56. ↑ 56.0 56.1 Hamburg, University of (2022-07-03). "Physicists Create Continuous Time Crystal for the First Time" (in en-us). https://scitechdaily.com/physicists-create-continuous-time-crystal-for-the-first-time/. 
  57. ↑ Autti, S.; Eltsov, V. B.; Volovik, G. E. (May 2018). "Observation of a Time Quasicrystal and Its Transition to a Superfluid Time Crystal". Physical Review Letters 120 (21): 215301. doi:10.1103/PhysRevLett.120.215301. PMID 29883148. Bibcode: 2018PhRvL.120u5301A. 
  58. ↑ Autti, S.; Heikkinen, P. J.; Mäkinen, J. T.; Volovik, G. E.; Zavjalov, V. V.; Eltsov, V. B. (February 2021). "AC Josephson effect between two superfluid time crystals". Nature Materials 20 (2): 171–174. doi:10.1038/s41563-020-0780-y. PMID 32807922. Bibcode: 2021NatMa..20..171A. 
  59. ↑ Träger, Nick; Gruszecki, Paweł; Lisiecki, Filip; Groß, Felix; Förster, Johannes; Weigand, Markus; Głowiński, Hubert; Kuświk, Piotr et al. (2021-02-03). "Real-Space Observation of Magnon Interaction with Driven Space–Time Crystals". Physical Review Letters 126 (5): 057201. doi:10.1103/PhysRevLett.126.057201. PMID 33605763. Bibcode: 2021PhRvL.126e7201T. https://link.aps.org/doi/10.1103/PhysRevLett.126.057201. 
  60. ↑ Williams, Jon (9 February 2021). "World's first video recording of a space–time crystal" (in en). https://is.mpg.de/news/world-s-first-video-recording-of-a-space-time-crystal. 
  61. ↑ Wolchover, Natalie (2021-07-30). "Eternal Change for No Energy: A Time Crystal Finally Made Real" (in en). https://www.quantamagazine.org/first-time-crystal-built-using-googles-quantum-computer-20210730/. 
  62. ↑ Kyprianidis, A.; Machado, F.; Morong, W.; Becker, P.; Collins, K. S.; Else, D. V.; Feng, L.; Hess, P. W. et al. (2021-06-11). "Observation of a prethermal discrete time crystal" (in en). Science 372 (6547): 1192–1196. doi:10.1126/science.abg8102. ISSN 0036-8075. PMID 34112691. Bibcode: 2021Sci...372.1192K. https://www.science.org/doi/10.1126/science.abg8102. 
  63. ↑ S, Robert; ers; Berkeley, U. C. (2021-11-10). "Creating Time Crystals Using New Quantum Computing Architectures" (in en-US). https://scitechdaily.com/creating-time-crystals-using-new-quantum-computing-architectures/. 
  64. ↑ Randall, J.; Bradley, C. E.; van der Gronden, F. V.; Galicia, A.; Abobeih, M. H.; Markham, M.; Twitchen, D. J.; Machado, F. et al. (2021-12-17). "Many-body–localized discrete time crystal with a programmable spin-based quantum simulator" (in en). Science 374 (6574): 1474–1478. doi:10.1126/science.abk0603. ISSN 0036-8075. PMID 34735218. Bibcode: 2021Sci...374.1474R. https://www.science.org/doi/10.1126/science.abk0603. 
  65. ↑ Boerkamp, Martijn (2021-11-17). "Physicists create discrete time crystals in a programmable quantum simulator" (in en-GB). Physics World. https://physicsworld.com/physicists-create-discrete-time-crystals-in-a-programmable-quantum-simulator/. 
  66. ↑ Starr, Michelle (16 February 2022). "New Breakthrough Could Bring Time Crystals Out of The Lab And Into The Real World" (in en-gb). https://www.sciencealert.com/time-crystals-have-been-observed-in-a-system-that-isn-t-isolated-from-its-environment. 
  67. ↑ Taheri, Hossein; Matsko, Andrey B.; Maleki, Lute; Sacha, Krzysztof (14 February 2022). "All-optical dissipative discrete time crystals" (in en). Nature Communications 13 (1): 848. doi:10.1038/s41467-022-28462-x. ISSN 2041-1723. PMID 35165273. Bibcode: 2022NatCo..13..848T. 
  68. ↑ (in en) Physicists produce biggest time crystal yet. 2022-03-02. doi:10.1126/science.adb1790. https://www.science.org/content/article/physicists-produce-biggest-time-crystal-yet. 
  69. ↑ Frey, Philipp; Rachel, Stephan (2022-03-04). "Realization of a discrete time crystal on 57 qubits of a quantum computer" (in en). Science Advances 8 (9): eabm7652. doi:10.1126/sciadv.abm7652. ISSN 2375-2548. PMID 35235347. Bibcode: 2022SciA....8M7652F. 
  70. ↑ Frey, Philipp; Rachel, Stephan (March 2, 2022). "'An ever-ticking clock': we made a 'time crystal' inside a quantum computer" (in en). http://theconversation.com/an-ever-ticking-clock-we-made-a-time-crystal-inside-a-quantum-computer-178164. 

Academic articles

Books

Press

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Time_crystal&oldid=3285236"