Physics:Quantum spin liquid
In condensed matter physics, a quantum spin liquid is a phase of matter that can be formed by interacting quantum spins in certain magnetic materials. Quantum spin liquids (QSL) are generally characterized by their long-range quantum entanglement, fractionalized excitations, and absence of ordinary magnetic order.[1]
The quantum spin liquid state was first proposed by physicist Phil Anderson in 1973 as the ground state for a system of spins on a triangular lattice that interact antiferromagnetically with their nearest neighbors, i.e. neighboring spins seek to be aligned in opposite directions.[2] Quantum spin liquids generated further interest when in 1987 Anderson proposed a theory that described high-temperature superconductivity in terms of a disordered spin-liquid state.[3][4]
Basic properties
File:Frustrated magnetism.webm
The simplest kind of magnetic phase is a paramagnet, where each individual spin behaves independently of the rest, just like atoms in an ideal gas. This highly disordered phase is the generic state of magnets at high temperatures, where thermal fluctuations dominate. Upon cooling, the spins will often enter a ferromagnet (or antiferromagnet) phase. In this phase, interactions between the spins cause them to align into large-scale patterns, such as domains, stripes, or checkerboards. These long-range patterns are referred to as "magnetic order," and are analogous to the regular crystal structure formed by many solids.[5]
Quantum spin liquids offer a dramatic alternative to this typical behavior. One intuitive description of this state is as a "liquid" of disordered spins, in comparison to a ferromagnetic spin state,[6] much in the way liquid water is in a disordered state compared to crystalline ice. However, unlike other disordered states, a quantum spin liquid state preserves its disorder to very low temperatures.[7] A more modern characterization of quantum spin liquids involves their topological order,[8] long-range quantum entanglement properties,[1] and anyon excitations.[9]
Examples
Several physical models have a disordered ground state that can be described as a quantum spin liquid.
Frustrated magnetic moments

Localized spins are frustrated if there exist competing exchange interactions that can not all be satisfied at the same time, leading to a large degeneracy of the system's ground state. A triangle of Ising spins (meaning that the only possible orientation of the spins are either "up" or "down"), which interact antiferromagnetically, is a simple example for frustration. In the ground state, two of the spins can be antiparallel but the third one cannot. This leads to an increase of possible orientations (six in this case) of the spins in the ground state, enhancing fluctuations and thus suppressing magnetic ordering.
A recent research work used this concept in analyzing brain networks and surprisingly indicated frustrated interactions in the brain corresponding to flexible neural interactions. This observation highlights the generalization of the frustration phenomenon and proposes its investigation in biological systems.[10]
Resonating valence bonds (RVB)

To build a ground state without magnetic moment, valence bond states can be used, where two electron spins form a spin 0 singlet due to the antiferromagnetic interaction. If every spin in the system is bound like this, the state of the system as a whole has spin 0 too and is non-magnetic. The two spins forming the bond are maximally entangled, while not being entangled with the other spins. If all spins are distributed to certain localized static bonds, this is called a valence bond solid (VBS).
There are two things that still distinguish a VBS from a spin liquid: First, by ordering the bonds in a certain way, the lattice symmetry is usually broken, which is not the case for a spin liquid. Second, this ground state lacks long-range entanglement. To achieve this, quantum mechanical fluctuations of the valence bonds must be allowed, leading to a ground state consisting of a superposition of many different partitionings of spins into valence bonds. If the partitionings are equally distributed (with the same quantum amplitude), there is no preference for any specific partitioning ("valence bond liquid"). This kind of ground state wavefunction was proposed by P. W. Anderson in 1973 as the ground state of spin liquids[2] and is called a resonating valence bond (RVB) state. These states are of great theoretical interest as they are proposed to play a key role in high-temperature superconductor physics.[4]
-
One possible short-range pairing of spins in a RVB state.
-
Long-range pairing of spins.
Excitations

The valence bonds do not have to be formed by nearest neighbors only and their distributions may vary in different materials. Ground states with large contributions of long range valence bonds have more low-energy spin excitations, as those valence bonds are easier to break up. On breaking, they form two free spins. Other excitations rearrange the valence bonds, leading to low-energy excitations even for short-range bonds. Something very special about spin liquids is that they support exotic excitations, meaning excitations with fractional quantum numbers. A prominent example is the excitation of spinons which are neutral in charge and carry spin . In spin liquids, a spinon is created if one spin is not paired in a valence bond. It can move by rearranging nearby valence bonds at low energy cost.
Realizations of (stable) RVB states
The first discussion of the RVB state on square lattice using the RVB picture[11] only consider nearest neighbour bonds that connect different sub-lattices. The constructed RVB state is an equal amplitude superposition of all the nearest-neighbour bond configurations. Such a RVB state is believed to contain emergent gapless gauge field which may confine the spinons etc. So the equal-amplitude nearest-neighbour RVB state on square lattice is unstable and does not corresponds to a quantum spin phase. It may describe a critical phase transition point between two stable phases. A version of RVB state which is stable and contains deconfined spinons is the chiral spin state.[12][13] Later, another version of stable RVB state with deconfined spinons, the Z2 spin liquid, is proposed,[14][15] which realizes the simplest topological order – Z2 topological order. Both chiral spin state and Z2 spin liquid state have long RVB bonds that connect the same sub-lattice. In chiral spin state, different bond configurations can have complex amplitudes, while in Z2 spin liquid state, different bond configurations only have real amplitudes. The RVB state on triangle lattice also realizes the Z2 spin liquid,[16] where different bond configurations only have real amplitudes. The toric code model is yet another realization of Z2 spin liquid (and Z2 topological order) that explicitly breaks the spin rotation symmetry and is exactly soluble.[17]
Experimental signatures and probes
Since there is no single experimental feature which identifies a material as a spin liquid, several experiments have to be conducted to gain information on different properties which characterize a spin liquid.[18]
Magnetic susceptibility
In a high-temperature, classical paramagnet phase, the magnetic susceptibility is given by the Curie–Weiss law
Fitting experimental data to this equation determines a phenomenological Curie–Weiss temperature, . There is a second temperature, , where magnetic order in the material begins to develop, as evidenced by a non-analytic feature in . The ratio of these is called the frustration parameter
In a classic antiferromagnet, the two temperatures should coincide and give . An ideal quantum spin liquid would not develop magnetic order at any temperature and so would have a diverging frustration parameter .[19] A large value is therefore a good indication of a possible spin liquid phase. Some frustrated materials with different lattice structures and their Curie–Weiss temperature are listed in the table below.[7] All of them are proposed spin liquid candidates.
| Material | Lattice | |
|---|---|---|
| κ-(BEDT-TTF)2Cu2(CN)3 | anisotropic triangular | -375 |
| ZnCu3(OH)6Cl2 (herbertsmithite) | Kagome | -241 |
| BaCu3V2O8(OH)2 (vesignieite) | Kagome | |
| Na4Ir3O8 | Hyperkagome | -650 |
| PbCuTe2O6 | Hyperkagome | -22[20] |
| Cu-(1,3-benzenedicarboxylate) | Kagome | -33[21] |
| Rb2Cu3SnF12 | Kagome | [22] |
| 1T-TaS2 | Triangular |
Other
One of the most direct evidence for absence of magnetic ordering give NMR or μSR experiments. If there is a local magnetic field present, the nuclear or muon spin would be affected which can be measured. 1H-NMR measurements[23] on κ-(BEDT-TTF)2Cu2(CN)3 have shown no sign of magnetic ordering down to 32 mK, which is four orders of magnitude smaller than the coupling constant J≈250 K[24] between neighboring spins in this compound. Further investigations include:
- Specific heat measurements give information about the low-energy density of states, which can be compared to theoretical models.
- Thermal transport measurements can determine if excitations are localized or itinerant.
- Neutron scattering gives information about the nature of excitations and correlations (e.g. spinons).
- Reflectance measurements can uncover spinons, which couple via emergent gauge fields to the electromagnetic field, giving rise to a power-law optical conductivity.[25]

Candidate materials
RVB type
Neutron scattering measurements of cesium chlorocuprate Cs2CuCl4, a spin-1/2 antiferromagnet on a triangular lattice, displayed diffuse scattering. This was attributed to spinons arising from a 2D RVB state.[26] Later theoretical work challenged this picture, arguing that all experimental results were instead consequences of 1D spinons confined to individual chains.[27]
Afterwards, it was observed in an organic Mott insulator (κ-(BEDT-TTF)2Cu2(CN)3) by Kanoda's group in 2003.[23] It may correspond to a gapless spin liquid with spinon Fermi surface (the so-called uniform RVB state).[2] The peculiar phase diagram of this organic quantum spin liquid compound was first thoroughly mapped using muon spin spectroscopy.[28]
Herbertsmithite
Herbertsmithite is one of the most extensively studied QSL candidate materials.[19] It is a mineral with chemical composition ZnCu3(OH)6Cl2 and a rhombohedral crystal structure. Notably, the copper ions within this structure form stacked two-dimensional layers of kagome lattices. Additionally, superexchange over the oxygen bonds creates a strong antiferromagnetic interaction between the copper spins within a single layer, whereas coupling between layers is negligible.[19] Therefore, it is a good realization of the antiferromagnetic spin-1/2 Heisenberg model on the kagome lattice, which is a prototypical theoretical example of a quantum spin liquid.[29][30]
Synthetic, polycrystalline herbertsmithite powder was first reported in 2005, and initial magnetic susceptibility studies showed no signs of magnetic order down to 2K.[31] In a subsequent study, the absence of magnetic order was verified down to 50 mK, inelastic neutron scattering measurements revealed a broad spectrum of low energy spin excitations, and low-temperature specific heat measurements had power law scaling. This gave compelling evidence for a spin liquid state with gapless spinon excitations.[32] A broad array of additional experiments, including 17O NMR,[33] and neutron spectroscopy of the dynamic magnetic structure factor,[34] reinforced the identification of herbertsmithite as a gapless spin liquid material, although the exact characterization remained unclear as of 2010.[35]
Large (millimeter size) single crystals of herbertsmithite were grown and characterized in 2011.[36] These enabled more precise measurements of possible spin liquid properties. In particular, momentum-resolved inelastic neutron scattering experiments showed a broad continuum of excitations. This was interpreted as evidence for gapless, fractionalized spinons.[37] Follow-up experiments (using 17O NMR and high-resolution, low-energy neutron scattering) refined this picture and determined there was actually a small spinon excitation gap of 0.07–0.09 meV.[38][39]
Some measurements were suggestive of quantum critical behavior.[40][41] Magnetic response of this material displays scaling relation in both the bulk ac susceptibility and the low energy dynamic susceptibility, with the low temperature heat capacity strongly depending on magnetic field.[42][43] This scaling is seen in certain quantum antiferromagnets, heavy-fermion metals, and two-dimensional 3He as a signature of proximity to a quantum critical point.[44]
In 2020, monodisperse single-crystal nanoparticles of herbertsmithite (~10 nm) were synthesized at room temperature, using gas-diffusion electrocrystallization, showing that their spin liquid nature persists at such small dimensions.[45]
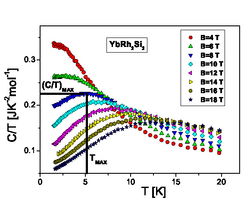

It may realize a U(1)-Dirac spin liquid.[48]
Kitaev spin liquids
Another evidence of quantum spin liquid was observed in a 2-dimensional material in August 2015. The researchers of Oak Ridge National Laboratory, collaborating with physicists from the University of Cambridge, and the Max Planck Institute for the Physics of Complex Systems in Dresden, Germany, measured the first signatures of these fractional particles, known as Majorana fermions, in a two-dimensional material with a structure similar to graphene. Their experimental results successfully matched with one of the main theoretical models for a quantum spin liquid, known as a Kitaev honeycomb model.[49][50]
Strongly correlated quantum spin liquid
The strongly correlated quantum spin liquid (SCQSL) is a specific realization of a possible quantum spin liquid (QSL)[7][40] representing a new type of strongly correlated electrical insulator (SCI) that possesses properties of heavy fermion metals with one exception: it resists the flow of electric charge.[47][51] At low temperatures T the specific heat of this type of insulator is proportional to Tn, with n less or equal 1 rather than n=3, as it should be in the case of a conventional insulator whose heat capacity is proportional to T3. When a magnetic field B is applied to SCI the specific heat depends strongly on B, contrary to conventional insulators. There are a few candidates of SCI; the most promising among them is Herbertsmithite,[51] a mineral with chemical structure ZnCu3(OH)6Cl2.
Kagome type
Ca10Cr7O28 is a frustrated kagome bilayer magnet, which does not develop long-range order even below 1 K, and has a diffuse spectrum of gapless excitations.
Toric code type
In December 2021, the first direct measurement of a quantum spin liquid of the toric code type was reported,[52][53] it was achieved by two teams: one exploring ground state and anyonic excitations on a quantum processor[54] and the other implementing a theoretical blueprint[55] of atoms on a ruby lattice held with optical tweezers on a quantum simulator.[56]
Specific properties: topological fermion condensation quantum phase transition
The experimental facts collected on heavy fermion (HF) metals and two dimensional Helium-3 demonstrate that the quasiparticle effective mass M* is very large, or even diverges. Topological fermion condensation quantum phase transition (FCQPT) preserves quasiparticles, and forms flat energy band at the Fermi level. The emergence of FCQPT is directly related to the unlimited growth of the effective mass M*.[44] Near FCQPT, M* starts to depend on temperature T, number density x, magnetic field B and other external parameters such as pressure P, etc. In contrast to the Landau paradigm based on the assumption that the effective mass is approximately constant, in the FCQPT theory the effective mass of new quasiparticles strongly depends on T, x, B etc. Therefore, to agree/explain with the numerous experimental facts, extended quasiparticles paradigm based on FCQPT has to be introduced. The main point here is that the well-defined quasiparticles determine the thermodynamic, relaxation, scaling and transport properties of strongly correlated Fermi systems and M* becomes a function of T, x, B, P, etc. The data collected for very different strongly correlated Fermi systems demonstrate universal scaling behavior; in other words distinct materials with strongly correlated fermions unexpectedly turn out to be uniform, thus forming a new state of matter that consists of HF metals, quasicrystals, quantum spin liquid, two-dimensional Helium-3, and compounds exhibiting high-temperature superconductivity.[40][44]
Applications
Materials supporting quantum spin liquid states may have applications in data storage and memory.[57] In particular, it is possible to realize topological quantum computation by means of spin-liquid states.[58] Developments in quantum spin liquids may also help in the understanding of high temperature superconductivity.[59]
References
- ↑ 1.0 1.1 Savary, L.; Balents, L. (2017). "Quantum spin liquids: a review". Reports on Progress in Physics 80 (1): 016502. doi:10.1088/0034-4885/80/1/016502. PMID 27823986. Bibcode: 2017RPPh...80a6502S.
- ↑ 2.0 2.1 2.2 P. W. Anderson (1973). "Resonating valence bonds: A new kind of insulator?". Materials Research Bulletin 8 (2): 153–160. doi:10.1016/0025-5408(73)90167-0.
- ↑ Trafton, Anne (March 28, 2011). "A new spin on superconductivity?". MIT News. http://web.mit.edu/newsoffice/2011/quantum-spin-liquid-0329.html.
- ↑ 4.0 4.1 P. W. Anderson (1987). "The resonating valence bond state in La2CuO4 and superconductivity". Science 235 (4793): 1196–1198. doi:10.1126/science.235.4793.1196. PMID 17818979. Bibcode: 1987Sci...235.1196A.
- ↑ Chaikin, Paul M; Lubensky, Tom C (1995). Principles of Condensed-Matter Physics. Cambridge university press. ISBN 9780521432245. https://archive.org/details/principlesofcond00chai.
- ↑ Wilkins, Alasdair (August 15, 2011). "A Strange New Quantum State of Matter: Spin Liquids". io9. http://io9.com/5831111/a-strange-new-quantum-state-of-matter-spin-liquids.
- ↑ 7.0 7.1 7.2 Leon Balents (2010). "Spin liquids in frustrated magnets". Nature 464 (7286): 199–208. doi:10.1038/nature08917. PMID 20220838. Bibcode: 2010Natur.464..199B.
- ↑ Wolchover, Natalie (2018-01-03). "Physicists Aim to Classify All Possible Phases of Matter". Quanta Magazine. https://www.quantamagazine.org/physicists-aim-to-classify-all-possible-phases-of-matter-20180103/.
- ↑ Wilczek, Frank (2017-02-28). "Inside the Knotty World of 'Anyon' Particles". Quanta Magazine. https://www.quantamagazine.org/how-anyon-particles-emerge-from-quantum-knots-20170228/.
- ↑ "Pattern of frustration formation in the functional brain network". Network Neuroscience 6 (4): 1334–1356. October 2022. doi:10.1162/netn_a_00268. https://direct.mit.edu/netn/article/6/4/1334/112207/Pattern-of-frustration-formation-in-the-functional.
- ↑ Kivelson, Steven A.; Rokhsar, Daniel S.; Sethna, James P. (1987). "Topology of the resonating valence-bond state: Solitons and high-Tc superconductivity". Physical Review B 35 (16): 8865–8868. doi:10.1103/physrevb.35.8865. PMID 9941277. Bibcode: 1987PhRvB..35.8865K.
- ↑ Kalmeyer, V.; Laughlin, R. B. (1987). "Equivalence of the resonating-valence-bond and fractional quantum Hall states". Physical Review Letters 59 (18): 2095–2098. doi:10.1103/physrevlett.59.2095. PMID 10035416. Bibcode: 1987PhRvL..59.2095K. https://zenodo.org/record/1233858.
- ↑ Wen, Xiao-Gang; Wilczek, F.; Zee, A. (1989). "Chiral Spin States and Superconductivity". Physical Review B 39 (16): 11413–11423. doi:10.1103/physrevb.39.11413. PMID 9947970. Bibcode: 1989PhRvB..3911413W.
- ↑ Read, N.; Sachdev, Subir (1991). "Large-N expansion for frustrated quantum antiferromagnets". Physical Review Letters 66 (13): 1773–1776. doi:10.1103/physrevlett.66.1773. PMID 10043303. Bibcode: 1991PhRvL..66.1773R.
- ↑ Wen, Xiao-Gang (1991). "Mean Field Theory of Spin Liquid States with Finite Energy Gaps". Physical Review B 44 (6): 2664–2672. doi:10.1103/physrevb.44.2664. PMID 9999836. Bibcode: 1991PhRvB..44.2664W.
- ↑ Moessner, R.; Sondhi, S. L. (2002). "Resonating Valence Bond Liquid Physics on the Triangular Lattice". Progress of Theoretical Physics Supplement 145: 37–42. doi:10.1143/PTPS.145.37. Bibcode: 2002PThPS.145...37M.
- ↑ Kitaev, A.Yu.; Balents, Leon (2003). "Fault-tolerant quantum computation by anyons". Annals of Physics 303 (1): 2–30. doi:10.1016/S0003-4916(02)00018-0. Bibcode: 2003AnPhy.303....2K.
- ↑ Knolle, Johannes; Moessner, Roderich (2019). "A field guide to spin liquids". Annual Review of Condensed Matter Physics 10: 451–472. doi:10.1146/annurev-conmatphys-031218-013401. Bibcode: 2019ARCMP..10..451K.
- ↑ 19.0 19.1 19.2 Norman, M.R. (2016). "Herbertsmithite and the Search for the Quantum Spin Liquid". Reviews of Modern Physics 88 (4): 041002. doi:10.1103/RevModPhys.88.041002.
- ↑ Phys. Rev. Lett. 116, 107203 (2016)
- ↑ Nytko, Emily A.; Helton, Joel S.; Müller, Peter; Nocera, Daniel G. (2008). "A Structurally Perfect S = 1/2 Metal−Organic Hybrid Kagome Antiferromagnet". Journal of the American Chemical Society 130 (10): 2922–2923. doi:10.1021/ja709991u. PMID 18275194.
- ↑ Matan, K.; Ono, T.; Fukumoto, Y.; Sato, T. J. et al. (2010). "Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice". Nature Physics 6 (11): 865–869. doi:10.1038/nphys1761. Bibcode: 2010NatPh...6..865M.
- ↑ 23.0 23.1 Y. Shimizu; K. Miyagawa; K. Kanoda; M. Maesato et al. (2003). "Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice". Physical Review Letters 91 (10): 107001. doi:10.1103/PhysRevLett.91.107001. PMID 14525498. Bibcode: 2003PhRvL..91j7001S.
- ↑ In literature, the value of J is commonly given in units of temperature () instead of energy.
- ↑ T. Ng; P. A. Lee (2007). "Power-Law Conductivity inside the Mott Gap: Application to κ-(BEDT-TTF)2Cu2(CN)3". Physical Review Letters 99 (15): 156402. doi:10.1103/PhysRevLett.99.156402. PMID 17995193. Bibcode: 2007PhRvL..99o6402N.
- ↑ Coldea, R.; Tennant, D.A.; Tsvelik, A.M.; Tylczynski, Z. (12 Feb 2001). "Experimental realization of a 2D fractional quantum spin liquid". Physical Review Letters 86 (7): 1335–1338. doi:10.1103/PhysRevLett.86.1335. PMID 11178077. Bibcode: 2001PhRvL..86.1335C. Note that the preprint was uploaded in 2000.
- ↑ Kohno, Masanori; Starkh, Oleg A; Balents, Leon (2007). "Spinons and triplons in spatially anisotropic frustrated antiferromagnets". Nature Physics 3 (11): 790. doi:10.1038/nphys749. Bibcode: 2007NatPh...3..790K.
- ↑ Pratt, F. L.; Baker, P. J.; Blundell, S. J.; Lancaster, T. et al. (2011). "Magnetic and non-magnetic phases of a quantum spin liquid". Nature 471 (7340): 612–616. doi:10.1038/nature09910. PMID 21455176. Bibcode: 2011Natur.471..612P.
- ↑ Elser, Veit (1989). "Nuclear antiferromagnetism in a registered 3He solid". Physical Review Letters 62 (20): 2405–2408. doi:10.1103/PhysRevLett.62.2405. PMID 10039977. Bibcode: 1989PhRvL..62.2405E.
- ↑ Yan, Simeng; Huse, David A; White, Steven R (2011). "Spin-liquid ground state of the S=1/2 kagome Heisenberg antiferromagnet". Science 332 (6034): 1173–1176. doi:10.1126/science.1201080. PMID 21527676. Bibcode: 2011Sci...332.1173Y.
- ↑ Shores, Matthew P; Nytko, Emily A; Bartlett, Bart M; Nocera, Daniel G (2005). "A Structurally Perfect S=1/2 Kagome Antigerromagnet". Journal of the American Chemical Society 127 (39): 13462–13463. doi:10.1021/ja053891p. PMID 16190686.
- ↑ Helton, J. S. (2007). "Spin Dynamics of the Spin-1/2 Kagome Lattice Antiferromagnet ZnCu3(OH)6Cl2". Physical Review Letters 98 (10): 107204. doi:10.1103/PhysRevLett.98.107204. PMID 17358563. Bibcode: 2007PhRvL..98j7204H.
- ↑ Olariu, A (2008). "17O NMR Study of the Intrinsic Magnetic Susceptibility and Spin Dynamics of the Quantum Kagome Antiferromagnet ZnCu3(OH)6Cl2". Physical Review Letters 100 (9): 087202. doi:10.1103/PhysRevLett.100.087202. PMID 18352658. Bibcode: 2008PhRvL.100h7202O.
- ↑ de Vries, M. A.; Stewart, J. R.; Deen, P. P.; Piatek, J. O.; Nilsen, G. J.; Ronnow, H. M.; Harrison, A. (2009). "Scale-free antiferromagnetic fluctuations in the S=1/2 kagome antiferromagnet herbertsmithite". Physical Review Letters 103 (23): 237201. doi:10.1103/PhysRevLett.103.237201. ISSN 0031-9007. PMID 20366167. Bibcode: 2009PhRvL.103w7201D.
- ↑ Mendels, Philippe; Bert, Fabrice (2010). "Quantum kagome antiferromagnet: ZnCu3(OH)6Cl2". Journal of the Physical Society of Japan 79 (1): 011001. doi:10.1143/JPSJ.79.011001. Bibcode: 2010JPSJ...79a1001M.
- ↑ Han, TH; Helton, JS; Chu, S; Prodi, Andrea; Singh, DK; Mazzoli, Claudio; Müller, P; Nocera, DG et al. (2011). "Synthesis and characterization of single crystals of the spin-1/2 kagome-lattice antiferromagnets Znx Cu4-x(OH)6Cl2". Physical Review B 83 (10): 100402. doi:10.1103/PhysRevB.83.100402. http://web.mit.edu/pmueller/www/own_papers/han_etal_2011.pdf.
- ↑ Han, Tian-Heng; Helton, Joel S; Chu, Shaoyan; Nocera, Daniel G; Rodriguez-Rivera, Jose A; Broholm, Collin; Lee, Young S (2012). "Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet". Nature 492 (7429): 406–410. doi:10.1038/nature11659. PMID 23257883. Bibcode: 2012Natur.492..406H.
- ↑ Fu, Mingxuan; Imai, Takashi; Lee, Young S (2015). "Evidence for a gapped spin-liquid ground state in a kagome Heisenberg antiferromagnet". Science 350 (6261): 655–658. doi:10.1126/science.aab2120. PMID 26542565. Bibcode: 2015Sci...350..655F.
- ↑ Han, Tian-Heng; Norman, MR; Wen, J-J; Rodriguez-Rivera, Jose A; Helton, Joel S; Broholm, Collin; Lee, Young S (2016). "Correlated impurities and intrinsic spin-liquid physics in the kagome material herbertsmithite". Physical Review B 94 (6): 060409. doi:10.1103/PhysRevB.94.060409. Bibcode: 2016PhRvB..94f0409H.
- ↑ 40.0 40.1 40.2 Amusia, M.; Popov, K.; Shaginyan, V.; Stephanovich, V. (2014). Theory of Heavy-Fermion Compounds - Theory of Strongly Correlated Fermi-Systems. Springer Series in Solid-State Sciences. 182. Springer. doi:10.1007/978-3-319-10825-4. ISBN 978-3-319-10825-4.
- ↑ Wen, Jinsheng; Yu, Shun-Li; Li, Shiyan; Yu, Weiqiang; Li, Jian-Xin (12 September 2019). "Experimental identification of quantum spin liquids" (in en). npj Quantum Materials 4 (1): 12. doi:10.1038/s41535-019-0151-6. ISSN 2397-4648. Bibcode: 2019npjQM...4...12W. http://www.nature.com/articles/s41535-019-0151-6.
- ↑ 42.0 42.1 Helton, J. S. (2010). "Dynamic Scaling in the Susceptibility of the Spin-1/2 Kagome Lattice Antiferromagnet Herbertsmithite". Physical Review Letters 104 (14): 147201. doi:10.1103/PhysRevLett.104.147201. PMID 20481955. Bibcode: 2010PhRvL.104n7201H.
- ↑ de Vries, M. A. (2008). "The magnetic ground state of an experimental S=1/2 kagomé antiferromagnet". Physical Review Letters 100 (15): 157205. doi:10.1103/PhysRevLett.100.157205. PMID 18518149. Bibcode: 2008PhRvL.100o7205D.
- ↑ 44.0 44.1 44.2 Shaginyan, V. R.; Amusia, M. Ya.; Msezane, A. Z.; Popov, K. G. (2010). "Scaling Behavior of Heavy Fermion Metals". Physics Reports 492 (2–3): 31. doi:10.1016/j.physrep.2010.03.001. Bibcode: 2010PhR...492...31S.
- ↑ Pozo, Guillermo; de la Presa, Patricia; Prato, Rafael; Morales, Irene; Marin, Pilar; Fransaer, Jan; Dominguez-Benetton, Xochitl (2020). "Spin transition nanoparticles made electrochemically". Nanoscale 12 (9): 5412–5421. doi:10.1039/C9NR09884D. PMID 32080699.
- ↑ Gegenwart, P. (2006). "High-field phase diagram of the heavy-fermion metal YbRh2Si2". New Journal of Physics 8 (9): 171. doi:10.1088/1367-2630/8/9/171. Bibcode: 2006NJPh....8..171G.
- ↑ 47.0 47.1 Shaginyan, V. R.; Msezane, A.; Popov, K. (2011). "Thermodynamic Properties of Kagome Lattice in ZnCu3(OH)6Cl2 Herbertsmithite". Physical Review B 84 (6): 060401. doi:10.1103/PhysRevB.84.060401. Bibcode: 2011PhRvB..84f0401S.
- ↑ Ying Ran, Michael Hermele, Patrick A. Lee, Xiao-Gang Wen, (2006), "Projected wavefunction study of Spin-1/2 Heisenberg model on the Kagome lattice", https://arxiv.org/abs/cond-mat/0611414
- ↑ "New state of matter detected in a two-dimensional material". http://phys.org/news/2016-04-state-two-dimensional-material.html.
- ↑ Banerjee, A.; Bridges, C. A.; Yan, J.-Q.; Aczel, A. A.; Li, L.; Stone, M. B.; Granroth, G. E.; Lumsden, M. D. et al. (2016). "Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet". Nature Materials 15 (7): 733–740. doi:10.1038/nmat4604. PMID 27043779. Bibcode: 2016NatMa..15..733B.
- ↑ 51.0 51.1 Shaginyan, V. R. (2012). "Identification of Strongly Correlated Spin Liquid in Herbertsmithite". EPL 97 (5): 56001. doi:10.1209/0295-5075/97/56001. Bibcode: 2012EL.....9756001S.
- ↑ Wood, Charlie (2021-12-02). "Realizing topologically ordered states on a quantum processor" (in en). Science 374 (6572): 1237–1241. doi:10.1126/science.abi8378. PMID 34855491. Bibcode: 2021Sci...374.1237S. https://www.quantamagazine.org/quantum-simulators-create-a-totally-new-phase-of-matter-20211202/. Retrieved 2021-12-04.
- ↑ Wood, Charlie (2021-12-02). "Quantum Simulators Create a Totally New Phase of Matter" (in en). https://www.quantamagazine.org/quantum-simulators-create-a-totally-new-phase-of-matter-20211202/.
- ↑ Satzinger, K. J.; Liu, Y.-J; Smith, A.; Knapp, C.; Newman, M.; Jones, C.; Chen, Z.; Quintana, C. et al. (2021-12-03). "Realizing topologically ordered states on a quantum processor". Science 374 (6572): 1237–1241. doi:10.1126/science.abi8378. PMID 34855491. Bibcode: 2021Sci...374.1237S. https://www.science.org/doi/10.1126/science.abi8378.
- ↑ Verresen, Ruben; Lukin, Mikhail D.; Vishwanath, Ashvin (2021-07-08). "Prediction of Toric Code Topological Order from Rydberg Blockade". Physical Review X 11 (3): 031005. doi:10.1103/PhysRevX.11.031005. Bibcode: 2021PhRvX..11c1005V. https://link.aps.org/doi/10.1103/PhysRevX.11.031005.
- ↑ Semeghini, G.; Levine, H.; Keesling, A.; Ebadi, S.; Wang, T. T.; Bluvstein, D.; Verresen, R.; Pichler, H. et al. (2021-12-03). "Probing topological spin liquids on a programmable quantum simulator". Science 374 (6572): 1242–1247. doi:10.1126/science.abi8794. PMID 34855494. Bibcode: 2021Sci...374.1242S. https://www.science.org/doi/10.1126/science.abi8794.
- ↑ Aguilar, Mario (December 20, 2012). "This Weird Crystal Demonstrates a New Magnetic Behavior That Works Like Magic". Gizmodo. https://gizmodo.com/quantum-spin-liquid/.
- ↑ Fendley, Paul. "Topological Quantum Computation from non-abelian anyons". University of Virginia. http://rockpile.phys.virginia.edu/trieste08.pdf.
- ↑ Chandler, David (December 20, 2012). "New kind of magnetism discovered: Experiments demonstrate 'quantum spin liquid'". Phys.org. http://phys.org/news/2012-12-kind-magnetism-quantum-liquid.html.
 |

