Chemistry:Ostwald ripening

Short description: Process by which small crystals dissolve in solution for the benefit of larger crystals

Ostwald ripening in palladium nanoparticles dissolved in formaldehyde at 6 (a), 24 (b), 48 (c) and 72 hours (d). The small palladium particles are being consumed as the larger ones grow bigger.

File:A-general-patterning-approach-by-manipulating-the-evolution-of-two-dimensional-liquid-foams-ncomms14110-s2.ogv

Ostwald ripening is a phenomenon observed in solid solutions and liquid sols that involves the change of an inhomogeneous structure over time, in that small crystals or sol particles first dissolve and then redeposit onto larger crystals or sol particles.

Dissolution of small crystals or sol particles and the redeposition of the dissolved species on the surfaces of larger crystals or sol particles was first described by Wilhelm Ostwald in 1896. For colloidal systems, Ostwald ripening is also found in water-in-oil emulsions, while flocculation is found in oil-in-water emulsions.

Mechanism

This thermodynamically-driven spontaneous process occurs because larger particles are more energetically favored than smaller particles. This stems from the fact that molecules on the surface of a particle are energetically less stable than the ones in the interior.

Cubic crystal structure (sodium chloride)

Consider a cubic crystal of atoms: all the atoms inside are bonded to 6 neighbours and are quite stable, but atoms on the surface are only bonded to 5 neighbors or fewer, which makes these surface atoms less stable. Large particles are more energetically favorable since, continuing with this example, more atoms are bonded to 6 neighbors and fewer atoms are at the unfavorable surface. As the system tries to lower its overall energy, molecules on the surface of a small particle (energetically unfavorable, with only 3 or 4 or 5 bonded neighbors) will tend to detach from the particle and diffuse into the solution.

Kelvin's equation describes the relationship between the radius of curvature and the chemical potential between the surface and the inner volume:

[math]\displaystyle{ \Delta \mu = \frac {2 \sigma \nu_\mathrm{at}} {r} }[/math]

where [math]\displaystyle{ \mu }[/math] corresponds to the chemical potential, [math]\displaystyle{ \sigma }[/math] to the surface tension, [math]\displaystyle{ \nu_\mathrm{at} }[/math] to the atomic volume and [math]\displaystyle{ r }[/math] to the radius of the particle. The chemical potential of an ideal solution can also be expressed as a function of the solute’s concentration if liquid and solid phases are in equilibrium.

[math]\displaystyle{ \mu = k_\mathrm{B}T\log(C_\mathrm{eq}) }[/math]

where [math]\displaystyle{ k_\mathrm{B} }[/math] corresponds to the Boltzmann Constant, [math]\displaystyle{ T }[/math] to the temperature and [math]\displaystyle{ C_\mathrm{eq} }[/math] to the solute concentration in a solution in which the solid and the liquid phase are in equilibrium.

Combining both expressions the following equation is obtained:

[math]\displaystyle{ k_\mathrm{B} T \log\left(\frac {C_\mathrm{eq}} {C_{\infty}} \right) = \frac {2 \sigma \nu_\mathrm{at}} {r} \rightarrow C_\mathrm{eq}(r) = C_\mathrm{eq}(\infty) \mathrm{e}^{\frac {2 \sigma \nu_\mathrm{at}} {r k_\mathrm{B} T}} }[/math]

Thus, the equilibrium concentration, [math]\displaystyle{ C_{eq} }[/math], is lower around bigger particles than it is around smaller particles.

[math]\displaystyle{ C_\mathrm{eq}(r) \gt C_\mathrm{eq} (R) }[/math]

where [math]\displaystyle{ r }[/math] and [math]\displaystyle{ R }[/math] are the particles radius, and [math]\displaystyle{ r \lt R }[/math]. Inferring from Fick’s first law of diffusion, the particles will move from big concentrations, corresponding to areas surrounding small particles, to small concentrations, corresponding to areas surrounding large nanoparticles. Thus, the small particles will tend to shrink while the big particles will grow. As a result, the average size of the nanoparticles in the solution will grow, and the dispersion of sizes will decrease. Therefore, if a solution is left for a long time, in the extreme case of [math]\displaystyle{ t \rightarrow \infty }[/math], its particles would evolve until they would finally form a single huge spherical particle to minimize the total surface area.

The history of research progress in quantitatively modeling Ostwald ripening is long, with many derivations. In 1958, Lifshitz and Slyozov performed a mathematical investigation of Ostwald ripening in the case where diffusion of material is the slowest process. They began by stating how a single particle grows in a solution. This equation describes where the boundary is between small, shrinking particles and large, growing particles. They finally conclude that the average radius of the particles ⟨R⟩, grows as follows:

[math]\displaystyle{ \langle R \rangle ^3 - \langle R \rangle _0 ^3 = \frac {8 \gamma c_{\infty}v^2D} {9R_g T} t }[/math]

where

[math]\displaystyle{ \langle R \rangle }[/math]	average radius of all the particles
[math]\displaystyle{ \gamma }[/math]	particle surface tension or surface energy
[math]\displaystyle{ c_{\infty} }[/math]	solubility of the particle material
[math]\displaystyle{ v }[/math]	molar volume of the particle material
[math]\displaystyle{ D }[/math]	diffusion coefficient of the particle material
[math]\displaystyle{ R_g }[/math]	ideal gas constant
[math]\displaystyle{ T }[/math]	absolute temperature and
[math]\displaystyle{ t }[/math]	time.

Note that the quantity ⟨R⟩³ is different from ⟨R³⟩, and only the former one can be used to calculate average volume, and that the statement that ⟨R⟩ goes as t^1/3 relies on ⟨R⟩₀ being zero; but because nucleation is a separate process from growth, this places ⟨R⟩₀ outside the bounds of validity of the equation. In contexts where the actual value of ⟨R⟩₀ is irrelevant, an approach that respects the meanings of all terms is to take the time derivative of the equation to eliminate ⟨R⟩₀ and t. Another such approach is to change the ⟨R⟩₀ to ⟨R⟩_i with the initial time i having a positive value.

Also contained in the Lifshitz and Slyozov derivation is an equation for the size distribution function f(R, t) of particles. For convenience, the radius of particles is divided by the average radius to form a new variable, ρ = R(⟨R⟩)⁻¹.

[math]\displaystyle{ f(R,t) = \frac {4}{9} \rho^2 \left(\frac {3}{3+\rho}\right)^\frac {7}{3} \left(\frac {1.5} {1.5 - \rho}\right)^\frac {11}{3} \exp \left(- \frac {1.5}{1.5 - \rho}\right), \rho \lt 1.5 }[/math]

Three years after that Lifshitz and Slyozov published their findings (in Russian, 1958), Carl Wagner performed his own mathematical investigation of Ostwald ripening, examining both systems where diffusion was slow and also where attachment and detachment at the particle surface was slow. Although his calculations and approach were different, Wagner came to the same conclusions as Lifshitz and Slyozov for slow-diffusion systems. This duplicate derivation went unnoticed for years because the two scientific papers were published on opposite sides of the Iron Curtain in 1961. It was not until 1975 that Kahlweit addressed the fact that the theories were identical and combined them into the Lifshitz-Slyozov-Wagner or LSW theory of Ostwald ripening. Many experiments and simulations have shown LSW theory to be robust and accurate. Even some systems that undergo spinodal decomposition have been shown to quantitatively obey LSW theory after initial stages of growth.

Wagner derived that when attachment and detachment of molecules is slower than diffusion, then the growth rate becomes

[math]\displaystyle{ \langle R \rangle ^2 = \frac {64 \gamma c_{\infty} v^2 k_s} {81 R_g T} t }[/math]

where k_s is the reaction rate constant of attachment with units of length per time. Since the average radius is usually something that can be measured in experiments, it is fairly easy to tell if a system is obeying the slow-diffusion equation or the slow-attachment equation. If the experimental data obeys neither equation, then it is likely that another mechanism is taking place and Ostwald ripening is not occurring.

Although LSW theory and Ostwald ripening were intended for solids ripening in a fluid, Ostwald ripening is also observed in liquid-liquid systems, for example, in an oil-in-water emulsion polymerization. In this case, Ostwald ripening causes the diffusion of monomers (i.e. individual molecules or atoms) from smaller droplets to larger droplets due to greater solubility of the single monomer molecules in the larger monomer droplets. The rate of this diffusion process is linked to the solubility of the monomer in the continuous (water) phase of the emulsion. This can lead to the destabilization of emulsions (for example, by creaming and sedimentation).

Specific examples

Oil droplets in pastis mixed with water grow by Ostwald ripening.

One example of Ostwald ripening is the re-crystallization of water within ice cream which gives old ice cream a gritty, crunchy texture. Larger ice crystals grow at the expense of smaller ones within the ice cream, creating a coarser texture.

Another gastronomical example is the ouzo effect, where the droplets in the cloudy microemulsion grow by Ostwald ripening.

In geology, it is the textural coarsening, aging or growth of phenocrysts and crystals in solid rock which is below the solidus temperature. It is often ascribed as a process in the formation of orthoclase megacrysts, as an alternative to the physical processes governing crystal growth from nucleation and growth rate thermochemical limitations.

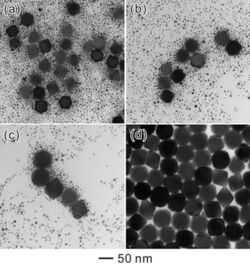
In aqueous solution chemistry and precipitates ageing, the term refers to the growth of larger crystals from those of smaller size which have a higher solubility than the larger ones. In the process, many small crystals formed initially (nuclei) slowly disappear, except for a few that grow larger, at the expense of the small crystals (crystal growth). The smaller crystals act as fuel for the growth of bigger crystals. Limiting Ostwald ripening is fundamental in modern technology for the solution synthesis of quantum dots. Ostwald ripening is also the key process in the digestion and aging of precipitates, an important step in gravimetric analysis. The digested precipitate is generally purer, and easier to wash and filter.

Ostwald ripening can also occur in emulsion systems, with molecules diffusing from small droplets to large ones through the continuous phase. When a miniemulsion is desired, an extremely hydrophobic compound is added to stop this process from taking place.

Diffusional growth of larger drops in liquid water clouds in the atmosphere at the expense of smaller drops is also characterized as Ostwald ripening.

See also

• Aggregation
• Coalescence
• Coalescence
• Critical radius
• Flocculation
• Kelvin equation
• Kirkendall effect
• Rock microstructure
• Solubility equilibrium § Particle size effect
• Nucleation
• Crystal growth
• Viedma ripening

External links

• Ostwald Ripening a 3D Kinetic Monte Carlo simulation