Physics:Eutectic system

Short description: Mixture with a lower melting point than its constituents

A phase diagram for a fictitious binary chemical mixture (with the two components denoted by A and B) used to depict the eutectic composition, temperature, and point. (L denotes the liquid state.)

A eutectic system or eutectic mixture (/juːˈtɛktɪk/ yoo-TEK-tik) is a homogeneous mixture that has a melting point lower than those of the constituents. The lowest possible melting point over all of the mixing ratios of the constituents is called the eutectic temperature. On a phase diagram, the eutectic temperature is seen as the eutectic point (see plot on the right).

Non-eutectic mixture ratios would have different melting temperatures for their different constituents, since one component's lattice will melt at a lower temperature than the other's. Conversely, as a non-eutectic mixture cools down, each of its components would solidify (form a lattice) at a different temperature, until the entire mass is solid.

Not all binary alloys have eutectic points, since the valence electrons of the component species are not always compatible, in any mixing ratio, to form a new type of joint crystal lattice. For example, in the silver-gold system the melt temperature (liquidus) and freeze temperature (solidus) "meet at the pure element endpoints of the atomic ratio axis while slightly separating in the mixture region of this axis".

The term eutectic was coined in 1884 by British physicist and chemist Frederick Guthrie (1833–1886). The word originates from el εὐ- (eû) 'well', and τῆξῐς (têxis) 'melting'.

Eutectic phase transition

Four eutectic structures: A) lamellar B) rod-like C) globular D) acicular.

The eutectic solidification is defined as follows:

[math]\displaystyle{ \text{Liquid} \quad \xrightarrow[\text{cooling}]{\text{eutectic} \atop \text{temperature}} \quad \alpha \text{ solid solution} \ + \ \beta \text{ solid solution} }[/math]

This type of reaction is an invariant reaction, because it is in thermal equilibrium; another way to define this is the change in Gibbs free energy equals zero. Tangibly, this means the liquid and two solid solutions all coexist at the same time and are in chemical equilibrium. There is also a thermal arrest for the duration of the change of phase during which the temperature of the system does not change.

The resulting solid macrostructure from a eutectic reaction depends on a few factors, with the most important factor being how the two solid solutions nucleate and grow. The most common structure is a lamellar structure, but other possible structures include rodlike, globular, and acicular.

Non-eutectic compositions

Compositions of eutectic systems that are not at the eutectic point can be classified as hypoeutectic or hypereutectic. Hypoeutectic compositions are those with a smaller percent composition of species β and a greater composition of species α than the eutectic composition (E) while hypereutectic solutions are characterized as those with a higher composition of species β and a lower composition of species α than the eutectic composition. As the temperature of a non-eutectic composition is lowered the liquid mixture will precipitate one component of the mixture before the other. In a hypereutectic solution, there will be a proeutectoid phase of species β whereas a hypoeutectic solution will have a proeutectic α phase.

Types

Alloys

Eutectic alloys have two or more materials and have a eutectic composition. When a non-eutectic alloy solidifies, its components solidify at different temperatures, exhibiting a plastic melting range. Conversely, when a well-mixed, eutectic alloy melts, it does so at a single, sharp temperature. The various phase transformations that occur during the solidification of a particular alloy composition can be understood by drawing a vertical line from the liquid phase to the solid phase on the phase diagram for that alloy.

Some uses include:

• NEMA Eutectic Alloy Overload Relays for electrical protection of 3-phase motors for pumps, fans, conveyors, and other factory process equipment.
• Eutectic alloys for soldering, both traditional alloys composed of lead (Pb) and tin (Sn), sometimes with additional silver (Ag) or gold (Au) — especially Sn₆₃Pb₃₇ and Sn₆₂Pb₃₆Ag₂ alloy formula for electronics - and newer lead-free soldering alloys, in particular ones composed of tin (Sn), silver (Ag), and copper (Cu) such as Sn_96.5Ag_3.5.
• Casting alloys, such as aluminium-silicon and cast iron (at the composition of 4.3% carbon in iron producing an austenite-cementite eutectic)
• Silicon chips are bonded to gold-plated substrates through a silicon-gold eutectic by the application of ultrasonic energy to the chip. See eutectic bonding.
• Brazing, where diffusion can remove alloying elements from the joint, so that eutectic melting is only possible early in the brazing process
• Temperature response, e.g., Wood's metal and Field's metal for fire sprinklers
• Non-toxic mercury replacements, such as galinstan
• Experimental glassy metals, with extremely high strength and corrosion resistance
• Eutectic alloys of sodium and potassium (NaK) that are liquid at room temperature and used as coolant in experimental fast neutron nuclear reactors.

Others

Solid–liquid phase change of ethanol–water mixtures

• Sodium chloride and water form a eutectic mixture whose eutectic point is −21.2 °C and 23.3% salt by mass. The eutectic nature of salt and water is exploited when salt is spread on roads to aid snow removal, or mixed with ice to produce low temperatures (for example, in traditional ice cream making).
• Ethanol–water has an unusually biased eutectic point, i.e. it is close to pure ethanol, which sets the maximum proof obtainable by fractional freezing.
• "Solar salt", 60% NaNO₃ and 40% KNO₃, forms a eutectic molten salt mixture which is used for thermal energy storage in concentrated solar power plants. To reduce the eutectic melting point in the solar molten salts, calcium nitrate is used in the following proportion: 42% Ca(NO₃)₂, 43% KNO_3, and 15% NaNO₃.
• Lidocaine and prilocaine—both are solids at room temperature—form a eutectic that is an oil with a 16 °C (61 °F) melting point that is used in eutectic mixture of local anesthetic (EMLA) preparations.
• Menthol and camphor, both solids at room temperature, form a eutectic that is a liquid at room temperature in the following proportions: 8:2, 7:3, 6:4, and 5:5. Both substances are common ingredients in pharmacy extemporaneous preparations.
• Minerals may form eutectic mixtures in igneous rocks, giving rise to characteristic intergrowth textures exhibited, for example, by granophyre.
• Some inks are eutectic mixtures, allowing inkjet printers to operate at lower temperatures.
• Choline chloride produces eutectic mixtures with many natural products such as citric acid, malic acid and sugars. These liquid mixtures can be used, for example, to obtain antioxidant and antidiabetic extracts from natural products.

Strengthening mechanisms

Alloys

The primary strengthening mechanism of the eutectic structure in metals is composite strengthening (See strengthening mechanisms of materials). This deformation mechanism works through load transfer between the two constituent phases where the more compliant phase transfers stress to the stiffer phase. By taking advantage of the strength of the stiff phase and the ductility of the compliant phase, the overall toughness of the material increases. As the composition is varied to either hypoeutectic or hypereutectic formations, the load transfer mechanism becomes more complex as there is now load transfer between the eutectic phase and the secondary phase as well as the load transfer within the eutectic phase itself.

A second tunable strengthening mechanism of eutectic structures is the spacing of the secondary phase. By changing the spacing of the secondary phase, the fraction of contact between the two phases through shared phase boundaries is also changed. By decreasing the spacing of the eutectic phase, creating a fine eutectic structure, more surface area is shared between the two constituent phases resulting in more effective load transfer. On the micro-scale, the additional boundary area acts as a barrier to dislocations further strengthening the material. As a result of this strengthening mechanism, coarse eutectic structures tend to be less stiff but more ductile while fine eutectic structures are stiffer but more brittle. The spacing of the eutectic phase can be controlled during processing as it is directly related to the cooling rate during solidification of the eutectic structure. For example, for a simple lamellar eutectic structure, the minimal lamellae spacing  is:

[math]\displaystyle{ \lambda^*=\frac{2\gamma V_m T_E }{\Delta H * \Delta T_0} }[/math]

Where  is [math]\displaystyle{ \gamma }[/math] is the surface energy of the two-phase boundary, [math]\displaystyle{ V_m }[/math] is the molar volume of the eutectic phase, [math]\displaystyle{ T_E }[/math]  is the solidification temperature of the eutectic phase, [math]\displaystyle{ \Delta H }[/math] is the enthalpy of formation of the eutectic phase, and [math]\displaystyle{ \Delta T_0 }[/math] is the undercooling of the material. So, by altering the undercooling, and by extension the cooling rate, the minimal achievable spacing of the secondary phase is controlled.

Strengthening metallic eutectic phases to resist deformation at high temperatures (see creep deformation) is more convoluted as the primary deformation mechanism changes depending on the level of stress applied. At high temperatures where deformation is dominated by dislocation movement, the strengthening from load transfer and secondary phase spacing remain as they continue to resist dislocation motion. At lower strains where Nabarro-Herring creep is dominant, the shape and size of the eutectic phase structure plays a significant role in material deformation as it affects the available boundary area for vacancy diffusion to occur.

Other critical points

Iron–carbon phase diagram, showing the eutectoid transformation between austenite (γ) and pearlite.

Eutectoid

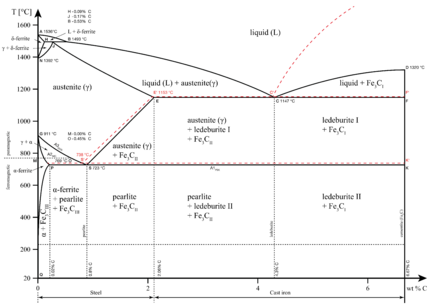
When the solution above the transformation point is solid, rather than liquid, an analogous eutectoid transformation can occur. For instance, in the iron-carbon system, the austenite phase can undergo a eutectoid transformation to produce ferrite and cementite, often in lamellar structures such as pearlite and bainite. This eutectoid point occurs at 723 °C (1,333 °F) and 0.76 wt% carbon.

Peritectoid

A peritectoid transformation is a type of isothermal reversible reaction that has two solid phases reacting with each other upon cooling of a binary, ternary, ..., n-ary alloy to create a completely different and single solid phase. The reaction plays a key role in the order and decomposition of quasicrystalline phases in several alloy types. A similar structural transition is also predicted for rotating columnar crystals.

Peritectic

Gold–aluminium phase diagram

Peritectic transformations are also similar to eutectic reactions. Here, a liquid and solid phase of fixed proportions react at a fixed temperature to yield a single solid phase. Since the solid product forms at the interface between the two reactants, it can form a diffusion barrier and generally causes such reactions to proceed much more slowly than eutectic or eutectoid transformations. Because of this, when a peritectic composition solidifies it does not show the lamellar structure that is found with eutectic solidification.

Such a transformation exists in the iron-carbon system, as seen near the upper-left corner of the figure. It resembles an inverted eutectic, with the δ phase combining with the liquid to produce pure austenite at 1,495 °C (2,723 °F) and 0.17% carbon.

At the peritectic decomposition temperature the compound, rather than melting, decomposes into another solid compound and a liquid. The proportion of each is determined by the lever rule. In the Al-Au phase diagram, for example, it can be seen that only two of the phases melt congruently, AuAl₂ and Au₂Al, while the rest peritectically decompose.

Eutectic calculation

The composition and temperature of a eutectic can be calculated from enthalpy and entropy of fusion of each components.

The Gibbs free energy G depends on its own differential:

[math]\displaystyle{ G = H - TS \Rightarrow \begin{cases} H = G + TS \\ \left(\frac{\partial G}{\partial T}\right)_P = -S \end{cases} \Rightarrow H = G - T \left(\frac{\partial G}{\partial T}\right)_P. }[/math]

Thus, the G/T derivative at constant pressure is calculated by the following equation:

[math]\displaystyle{ \left(\frac{\partial G / T}{\partial T}\right)_P = \frac{1}{T} \left(\frac{\partial G}{\partial T}\right)_P - \frac{1}{T^2}G = -\frac{1}{T^2} \left(G - T\left(\frac{\partial G}{\partial T}\right)_P\right) = -\frac{H}{T^2}. }[/math]

The chemical potential [math]\displaystyle{ \mu_i }[/math] is calculated if we assume that the activity is equal to the concentration:

[math]\displaystyle{ \mu_i = \mu_i^\circ + RT\ln \frac{a_i}{a} \approx \mu_i^\circ + RT\ln x_i. }[/math]

At the equilibrium, [math]\displaystyle{ \mu_i = 0 }[/math], thus [math]\displaystyle{ \mu_i^\circ }[/math] is obtained as

[math]\displaystyle{ \mu _i = \mu _i^\circ + RT\ln x_i = 0 \Rightarrow \mu_i^\circ = -RT\ln x_i. }[/math]

Using and integrating gives

[math]\displaystyle{ \left(\frac{\partial \mu_i / T}{\partial T}\right)_P = \frac{\partial}{\partial T}\left(R\ln x_i\right) \Rightarrow R\ln x_i = -\frac{H_i^\circ}{T} + K. }[/math]

The integration constant K may be determined for a pure component with a melting temperature [math]\displaystyle{ T^\circ }[/math] and an enthalpy of fusion [math]\displaystyle{ H^\circ }[/math]:

[math]\displaystyle{ x_i = 1 \Rightarrow T = T_i^\circ \Rightarrow K = \frac{H_i^\circ}{T_i^\circ}. }[/math]

We obtain a relation that determines the molar fraction as a function of the temperature for each component:

[math]\displaystyle{ R\ln x_i = -\frac{H_i^\circ}{T} + \frac{H_i^\circ}{T_i^\circ}. }[/math]

The mixture of n components is described by the system

[math]\displaystyle{ \begin{cases} \ln x_i + \frac{H_i^\circ}{RT} - \frac{H_i^\circ}{RT_i^\circ } = 0, \\ \sum\limits_{i = 1}^n x_i = 1. \end{cases} }[/math]

[math]\displaystyle{ \begin{cases} \forall i \lt n \Rightarrow \ln x_i + \frac{H_i^\circ}{RT} - \frac{H_i^\circ}{RT_i^\circ} = 0, \\ \ln \left(1 - \sum\limits_{i = 1}^{n - 1} x_i\right) + \frac{H_n^\circ}{RT} - \frac{H_n^\circ}{RT_n^\circ} = 0, \end{cases} }[/math]

which can be solved by

[math]\displaystyle{ \begin{array}{c} \left[ {{\begin{array}{*{20}c} {\Delta x_1 } \\ {\Delta x_2 } \\ {\Delta x_3 } \\ \vdots \\ {\Delta x_{n - 1} } \\ {\Delta T} \\ \end{array} }} \right] = \left[ {{\begin{array}{*{20}c} {1 / x_1 } & 0 & 0 & 0 & 0 & { - \frac{H_1^\circ }{RT^{2}}} \\ 0 & {1 / x_2 } & 0 & 0 & 0 & { - \frac{H_2^\circ }{RT^{2}}} \\ 0 & 0 & {1 / x_3 } & 0 & 0 & { - \frac{H_3^\circ }{RT^{2}}} \\ \vdots & \ddots & \ddots & \ddots & \ddots & { \vdots} \\ 0 & 0 & 0 & 0 & {1 / x_{n - 1} } & { - \frac{H_{n - 1}^\circ }{RT^{2}}} \\ {\frac{ - 1}{1 - \sum\limits_{i = 1}^{n - 1} {x_i } }} & {\frac{ - 1}{1 - \sum\limits_{i = 1}^{n - 1} {x_i } }} & {\frac{ - 1}{1 - \sum\limits_{i = 1}^{n - 1} {x_i } }} & {\frac{ - 1}{1 - \sum\limits_{i = 1}^{n - 1} {x_i } }} & {\frac{ - 1}{1 - \sum\limits_{i = 1}^{n - 1} {x_i } }} & { - \frac{H_n^\circ }{RT^{2}}} \\ \end{array} }} \right]^{ - 1} .\left[ {{\begin{array}{*{20}c} {\ln x_1 + \frac{H_1 ^\circ }{RT} - \frac{H_1^\circ }{RT_1^\circ }} \\ {\ln x_2 + \frac{H_2 ^\circ }{RT} - \frac{H_2^\circ }{RT_2^\circ }} \\ {\ln x_3 + \frac{H_3 ^\circ }{RT} - \frac{H_3^\circ }{RT_3^\circ }} \\ \vdots \\ {\ln x_{n - 1} + \frac{H_{n - 1} ^\circ }{RT} - \frac{H_{n - 1}^\circ }{RT_{n - 1}^\circ }} \\ {\ln \left({1 - \sum\limits_{i = 1}^{n - 1} {x_i } } \right) + \frac{H_n ^\circ }{RT} - \frac{H_n^\circ }{RT_n^\circ }} \\ \end{array} }} \right] \end{array} }[/math]

See also

• Azeotrope, or constant boiling mixture
• Freezing-point depression
• Low melting alloy

References

Bibliography

• Smith, William F.; Hashemi, Javad (2006), Foundations of Materials Science and Engineering (4th ed.), McGraw-Hill, ISBN 978-0-07-295358-9. 

Further reading

• Askeland, Donald R.; Pradeep P. Phule (2005). The Science and Engineering of Materials. Thomson-Engineering. ISBN 978-0-534-55396-8. 
• Easterling, Edward (1992). Phase Transformations in Metals and Alloys. CRC. ISBN 978-0-7487-5741-1. 
• Mortimer, Robert G. (2000). Physical Chemistry. Academic Press. ISBN 978-0-12-508345-4. 
• Reed-Hill, R. E.; Reza Abbaschian (1992). Physical Metallurgy Principles. Thomson-Engineering. ISBN 978-0-534-92173-6. 
• Sadoway, Donald (2004). "Phase Equilibria and Phase Diagrams". 3.091 Introduction to Solid State Chemistry, Fall 2004. MIT Open Courseware. http://ocw.mit.edu/NR/rdonlyres/Materials-Science-and-Engineering/3-091Fall-2004/6ECFB930-9D59-4DD5-A872-FE48002587B0/0/notes_10.pdf.