Chemistry:Energy profile
In theoretical chemistry, an energy profile is a theoretical representation of a chemical reaction or process as a single energetic pathway as the reactants are transformed into products. This pathway runs along the reaction coordinate, which is a parametric curve that follows the pathway of the reaction and indicates its progress; thus, energy profiles are also called reaction coordinate diagrams. They are derived from the corresponding potential energy surface (PES), which is used in computational chemistry to model chemical reactions by relating the energy of a molecule(s) to its structure (within the Born–Oppenheimer approximation).
Qualitatively, the reaction coordinate diagrams (one-dimensional energy surfaces) have numerous applications. Chemists use reaction coordinate diagrams as both an analytical and pedagogical aid for rationalizing and illustrating kinetic and thermodynamic events. The purpose of energy profiles and surfaces is to provide a qualitative representation of how potential energy varies with molecular motion for a given reaction or process.[1]
Potential energy surfaces
In simplest terms, a potential energy surface or PES is a mathematical or graphical representation of the relation between energy of a molecule and its geometry. The methods for describing the potential energy are broken down into a classical mechanics interpretation (molecular mechanics) and a quantum mechanical interpretation. In the quantum mechanical interpretation an exact expression for energy can be obtained for any molecule derived from quantum principles (although an infinite basis set may be required) but ab initio calculations/methods will often use approximations to reduce computational cost.[2][3] Molecular mechanics is empirically based and potential energy is described as a function of component terms that correspond to individual potential functions such as torsion, stretches, bends, Van der Waals energies, electrostatics and cross terms.[3][4][5] Each component potential function is fit to experimental data or properties predicted by ab initio calculations.[4] Molecular mechanics is useful in predicting equilibrium geometries and transition states as well as relative conformational stability. As a reaction occurs the atoms of the molecules involved will generally undergo some change in spatial orientation through internal motion as well as its electronic environment.[1] Distortions in the geometric parameters result in a deviation from the equilibrium geometry (local energy minima). These changes in geometry of a molecule or interactions between molecules are dynamic processes which call for understanding all the forces operating within the system. Since these forces can be mathematically derived as first derivative of potential energy with respect to a displacement, it makes sense to map the potential energy E of the system as a function of geometric parameters q1, q2, q3 and so on.[1] The potential energy at given values of the geometric parameters (q1, q2, ..., qn) is represented as a hyper-surface (when n > 2) or a surface (when n ≤ 2). Mathematically, it can be written as
- [math]\displaystyle{ E= f(q_1, q_2, \dots, q_n) }[/math]
For the quantum mechanical interpretation, a PES is typically defined within the Born–Oppenheimer approximation (in order to distinguish between nuclear and electronic motion and energy) which states that the nuclei are stationary relative to the electrons. In other words, the approximation allows the kinetic energy of the nuclei (or movement of the nuclei) to be neglected and therefore the nuclei repulsion is a constant value (as static point charges) and is only considered when calculating the total energy of the system. The electronic energy is then taken to depend parametrically on the nuclear coordinates, meaning a new electronic energy (Ee) must be calculated for each corresponding atomic configuration.[2][3]
PES is an important concept in computational chemistry and greatly aids in geometry and transition state optimization.
Degrees of freedom
An n-atom system is defined by 3n coordinates: (x, y, z) for each atom. These 3n degrees of freedom can be broken down to include 3 overall translational and 3 (or 2) overall rotational degrees of freedom for a non-linear system (for a linear system). However, overall translational or rotational degrees do not affect the potential energy of the system, which only depends on its internal coordinates. Thus an n-atom system will be defined by 3n – 6 (non-linear) or 3n – 5 (linear) coordinates.[1][3] These internal coordinates may be represented by simple stretch, bend, torsion coordinates, or symmetry-adapted linear combinations, or redundant coordinates, or normal modes coordinates, etc. For a system described by n-internal coordinates a separate potential energy function can be written with respect to each of these coordinates by holding the other n – 1 parameters at a constant value allowing the potential energy contribution from a particular molecular motion (or interaction) to be monitored while the other n – 1 parameters are defined.
Consider a diatomic molecule AB which can macroscopically visualized as two balls (which depict the two atoms A and B) connected through a spring which depicts the bond. As this spring (or bond) is stretched or compressed, the potential energy of the ball-spring system (AB molecule) changes and this can be mapped on a 2-dimensional plot as a function of distance between A and B, i.e. bond length.
The concept can be expanded to a tri-atomic molecule such as water where we have two O–H bonds and H–O–H bond angle as variables on which the potential energy of a water molecule will depend. We can safely assume the two O–H bonds to be equal. Thus, a PES can be drawn mapping the potential energy E of a water molecule as a function of two geometric parameters, q1 = O–H bond length and q2 = H–O–H bond angle. The lowest point on such a PES will define the equilibrium structure of a water molecule.
The same concept is applied to organic compounds like ethane, butane etc. to define their lowest energy and most stable conformations.
Characterizing a PES
The most important points on a PES are the stationary points where the surface is flat, i.e. parallel to a horizontal line corresponding to one geometric parameter, a plane corresponding to two such parameters or even a hyper-plane corresponding to more than two geometric parameters. The energy values corresponding to the transition states and the ground state of the reactants and products can be found using the potential energy function by calculating the function's critical points or the stationary points. Stationary points occur when the 1st partial derivative of the energy with respect to each geometric parameter is equal to zero.
- [math]\displaystyle{ \frac{\partial E}{\partial q_1}=\frac{\partial E}{\partial q_2}=\dots =\frac{\partial E}{\partial q_n}=0 }[/math]
Using analytical derivatives of the derived expression for energy, [math]\displaystyle{ E=f(q_1,q_2,\dots ,q_n), }[/math] one can find and characterize a stationary point as minimum, maximum or a saddle point. The ground states are represented by local energy minima and the transition states by saddle points.
Minima represent stable or quasi-stable species, i.e. reactants and products with finite lifetime. Mathematically, a minimum point is given as
- [math]\displaystyle{ \frac{\partial E}{\partial q_1}=0 }[/math]
- [math]\displaystyle{ \frac{\partial^2E}{\partial q_1^2}\gt 0 }[/math]
A point may be local minimum when it is lower in energy compared to its surrounding only or a global minimum which is the lowest energy point on the entire potential energy surface.
Saddle point represents a maximum along only one direction (that of the reaction coordinate) and is a minimum along all other directions. In other words, a saddle point represents a transition state along the reaction coordinate. Mathematically, a saddle point occurs when
- [math]\displaystyle{ \frac{\partial^2E}{\partial q^2}\gt 0 }[/math]
for all q except along the reaction coordinate and
- [math]\displaystyle{ \frac{\partial^2E}{\partial q_1^2}\lt 0 }[/math]
along the reaction coordinate.
Reaction coordinate diagrams
The intrinsic reaction coordinate[6] (IRC), derived from the potential energy surface, is a parametric curve that connects two energy minima in the direction that traverses the minimum energy barrier (or shallowest ascent) passing through one or more saddle point(s). However, in reality if reacting species attains enough energy it may deviate from the IRC to some extent.[1] The energy values (points on the hyper-surface) along the reaction coordinate result in a 1-D energy surface (a line) and when plotted against the reaction coordinate (energy vs reaction coordinate) gives what is called a reaction coordinate diagram (or energy profile). Another way of visualizing an energy profile is as a cross section of the hyper surface, or surface, long the reaction coordinate. Figure 5 shows an example of a cross section, represented by the plane, taken along the reaction coordinate and the potential energy is represented as a function or composite of two geometric variables to form a 2-D energy surface. In principle, the potential energy function can depend on N variables but since an accurate visual representation of a function of 3 or more variables cannot be produced (excluding level hypersurfaces) a 2-D surface has been shown. The points on the surface that intersect the plane are then projected onto the reaction coordinate diagram (shown on the right) to produce a 1-D slice of the surface along the IRC. The reaction coordinate is described by its parameters, which are frequently given as a composite of several geometric parameters, and can change direction as the reaction progresses so long as the smallest energy barrier (or activation energy (Ea)) is traversed.[1] The saddle point represents the highest energy point lying on the reaction coordinate connecting the reactant and product; this is known as the transition state. A reaction coordinate diagram may also have one or more transient intermediates which are shown by high energy wells connected via a transition state peak. Any chemical structure that lasts longer than the time for typical bond vibrations (10−13 – 10−14s) can be considered as intermediate.[4]
A reaction involving more than one elementary step has one or more intermediates being formed which, in turn, means there is more than one energy barrier to overcome. In other words, there is more than one transition state lying on the reaction pathway. As it is intuitive that pushing over an energy barrier or passing through a transition state peak would entail the highest energy, it becomes clear that it would be the slowest step in a reaction pathway. However, when more than one such barrier is to be crossed, it becomes important to recognize the highest barrier which will determine the rate of the reaction. This step of the reaction whose rate determines the overall rate of reaction is known as rate determining step or rate limiting step. The height of energy barrier is always measured relative to the energy of the reactant or starting material. Different possibilities have been shown in figure 6.

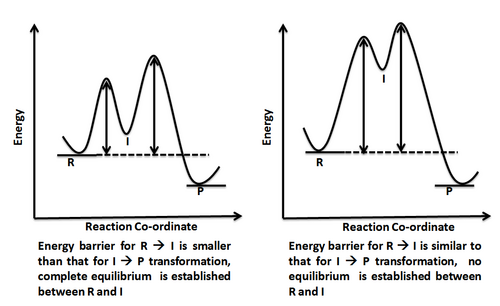
Reaction coordinate diagrams also give information about the equilibrium between a reactant or a product and an intermediate. If the barrier energy for going from intermediate to product is much higher than the one for reactant to intermediate transition, it can be safely concluded that a complete equilibrium is established between the reactant and intermediate. However, if the two energy barriers for reactant-to-intermediate and intermediate-to-product transformation are nearly equal, then no complete equilibrium is established and steady state approximation is invoked to derive the kinetic rate expressions for such a reaction.[7]
Drawing a reaction coordinate diagram
Although a reaction coordinate diagram is essentially derived from a potential energy surface, it is not always feasible to draw one from a PES. A chemist draws a reaction coordinate diagram for a reaction based on the knowledge of free energy or enthalpy change associated with the transformation which helps him to place the reactant and product into perspective and whether any intermediate is formed or not. One guideline for drawing diagrams for complex reactions is the principle of least motion which says that a favored reaction proceeding from a reactant to an intermediate or from one intermediate to another or product is one which has the least change in nuclear position or electronic configuration. Thus, it can be said that the reactions involving dramatic changes in position of nuclei actually occur through a series of simple chemical reactions. Hammond postulate is another tool which assists in drawing the energy of a transition state relative to a reactant, an intermediate or a product. It states that the transition state resembles the reactant, intermediate or product that it is closest in energy to, as long the energy difference between the transition state and the adjacent structure is not too large. This postulate helps to accurately predict the shape of a reaction coordinate diagram and also gives an insight into the molecular structure at the transition state.
Kinetic and thermodynamic considerations
A chemical reaction can be defined by two important parameters- the Gibbs free energy associated with a chemical transformation and the rate of such a transformation. These parameters are independent of each other. While free energy change describes the stability of products relative to reactants, the rate of any reaction is defined by the energy of the transition state relative to the starting material. Depending on these parameters, a reaction can be favorable or unfavorable, fast or slow and reversible or irreversible, as shown in figure 8.
A favorable reaction is one in which the change in free energy ∆G° is negative (exergonic) or in other words, the free energy of product, G°product, is less than the free energy of the starting materials, G°reactant. ∆G°> 0 (endergonic) corresponds to an unfavorable reaction. The ∆G° can be written as a function of change in enthalpy (∆H°) and change in entropy (∆S°) as ∆G°= ∆H° – T∆S°. Practically, enthalpies, not free energy, are used to determine whether a reaction is favorable or unfavorable, because ∆H° is easier to measure and T∆S° is usually too small to be of any significance (for T < 100 °C). A reaction with ∆H°<0 is called exothermic reaction while one with ∆H°>0 is endothermic.

The relative stability of reactant and product does not define the feasibility of any reaction all by itself. For any reaction to proceed, the starting material must have enough energy to cross over an energy barrier. This energy barrier is known as activation energy (∆G≠) and the rate of reaction is dependent on the height of this barrier. A low energy barrier corresponds to a fast reaction and high energy barrier corresponds to a slow reaction. A reaction is in equilibrium when the rate of forward reaction is equal to the rate of reverse reaction. Such a reaction is said to be reversible. If the starting material and product(s) are in equilibrium then their relative abundance is decided by the difference in free energy between them. In principle, all elementary steps are reversible, but in many cases the equilibrium lies so much towards the product side that the starting material is effectively no longer observable or present in sufficient concentration to have an effect on reactivity. Practically speaking, the reaction is considered to be irreversible.
While most reversible processes will have a reasonably small K of 103 or less, this is not a hard and fast rule, and a number of chemical processes require reversibility of even very favorable reactions. For instance, the reaction of an carboxylic acid with amines to form a salt takes place with K of 105–6, and at ordinary temperatures, this process is regarded as irreversible. Yet, with sufficient heating, the reverse reaction takes place to allow formation of the tetrahedral intermediate and, ultimately, amide and water. (For an extreme example requiring reversibility of a step with K > 1011, see demethylation.) A reaction can also be rendered irreversible if a subsequent, faster step takes place to consume the initial product(s), or a gas is evolved in an open system. Thus, there is no value of K that serves as a "dividing line" between reversible and irreversible processes. Instead, reversibility depends on timescale, temperature, the reaction conditions, and the overall energy landscape.
When a reactant can form two different products depending on the reaction conditions, it becomes important to choose the right conditions to favor the desired product. If a reaction is carried out at relatively lower temperature, then the product formed is one lying across the smaller energy barrier. This is called kinetic control and the ratio of the products formed depends on the relative energy barriers leading to the products. Relative stabilities of the products do not matter. However, at higher temperatures the molecules have enough energy to cross over both energy barriers leading to the products. In such a case, the product ratio is determined solely by the energies of the products and energies of the barrier do not matter. This is known as thermodynamic control and it can only be achieved when the products can inter-convert and equilibrate under the reaction condition. A reaction coordinate diagram can also be used to qualitatively illustrate kinetic and thermodynamic control in a reaction.

Applications
Following are few examples on how to interpret reaction coordinate diagrams and use them in analyzing reactions.
Solvent Effect: In general, if the transition state for the rate determining step corresponds to a more charged species relative to the starting material then increasing the polarity of the solvent will increase the rate of the reaction since a more polar solvent be more effective at stabilizing the transition state (ΔG‡ would decrease). If the transition state structure corresponds to a less charged species then increasing the solvents polarity would decrease the reaction rate since a more polar solvent would be more effective at stabilizing the starting material (ΔGo would decrease which in turn increases ΔG‡).[8]
SN1 vs SN2
The SN1 and SN2 mechanisms are used as an example to demonstrate how solvent effects can be indicated in reaction coordinate diagrams.
- SN1: Figure 10 shows the rate determining step for an SN1 mechanism, formation of the carbocation intermediate, and the corresponding reaction coordinate diagram. For an SN1 mechanism the transition state structure shows a partial charge density relative to the neutral ground state structure. Therefore, increasing the solvent polarity, for example from hexanes (shown as blue) to ether (shown in red), would decrease the rate of the reaction. As shown in figure 9, the starting material has approximately the same stability in both solvents (therefore ΔΔGo=ΔGopolar - ΔGonon polar is small) and the transition state is stabilized more in ether meaning ΔΔG≠ = ΔG≠polar - ΔG≠non-polar is large.
- SN2: For an SN2 mechanism a strongly basic nucleophile (i.e. a charged nucleophile) is favorable. In figure 11 below the rate determining step for Williamson ether synthesis is shown.[9][10] The starting material is methyl chloride and an ethoxide ion which has a localized negative charge meaning it is more stable in polar solvents. The figure shows a transition state structure as the methyl chloride undergoes nucleophilic attack. In the transition state structure the charge is distributed between the Cl and the O atoms and the more polar solvent is less effective at stabilizing the transition state structure relative to the starting materials. In other words, the energy difference between the polar and non-polar solvent is greater for the ground state (for the starting material) than in the transition state.
Catalysts: There are two types of catalysts, positive and negative. Positive catalysts increase the reaction rate and negative catalysts (or inhibitors) slow down a reaction and possibly cause the reaction not occur at all. The purpose of a catalyst is to alter the activation energy. Figure 12 illustrates the purpose of a catalyst in that only the activation energy is changed and not the relative thermodynamic stabilities, shown in the figure as ΔH, of the products and reactants. This means that a catalyst will not alter the equilibrium concentrations of the products and reactants but will only allow the reaction to reach equilibrium faster. Figure 13 shows the catalyzed pathway occurring in multiple steps which is a more realistic depiction of a catalyzed process. The new catalyzed pathway can occur through the same mechanism as the uncatalyzed reaction or through an alternate mechanism.[4] An enzyme is a biological catalyst that increases the rate for many vital biochemical reactions. Figure 13 shows a common way to illustrate the effect of an enzyme on a given biochemical reaction.[11]
See also
- Gibbs free energy
- Enthalpy
- Entropy
- Computational chemistry
- Molecular mechanics
- Born–Oppenheimer approximation
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Lewars, E.G. (2011). Computational Chemistry. Springer. pp. 9–43. ISBN 978-9048138616. https://www.springer.com/chemistry/theoretical+and+computational+chemistry/book/978-90-481-3860-9.
- ↑ 2.0 2.1 Szabo, Attila; Ostlund, Neil (1989). Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. Dover. ISBN 0-486-69186-1.
- ↑ 3.0 3.1 3.2 3.3 Sherrill, David. "Potential Energy Surfaces". http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/pes-lecture.pdf. Retrieved 2013-10-27.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Anslyn, Dougherty, Eric, Dennis (2006). Modern Physical Organic Chemistry. University Science Books. ISBN 1-891389-31-9.
- ↑ Sherrill, David. "Introduction to Molecular Mechanics". http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/molmech-lecture.pdf.
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Intrinsic reaction coordinate". doi:10.1351/goldbook.IT07057
- ↑ 7.0 7.1 Grossman, Robert (31 July 2007). The Art of Writing Reasonable Organic Reaction Mechanisms, 2nd ed. Springer. ISBN 978-0-387-95468-4. https://archive.org/details/artofwritingreas00gros.
- ↑ Bruice, Paula (2007). Organic Chemistry, 5th ed.. NJ: Pearson Prentice Hall. ISBN 978-0-13-196316-0.
- ↑ Neuman, Robert (2013). Organic Chemistry. Robert C. Neuman, Jr.. pp. Ch.7, 1–71. http://web.chem.ucsb.edu/~neuman/orgchembyneuman/BookContents.html.
- ↑ Organic Chemistry Portal. "Nucleophilic Substitution". https://www.organic-chemistry.org/namedreactions/nucleophilic-substitution-sn1-sn2.shtm. Retrieved 2013-10-25.
- ↑ Silverman, Richard (2004). The Organic Chemistry of Drug Design and Drug Action, 2nd ed. Elsevier. p. 178. ISBN 0-12-643732-7. https://archive.org/details/organicchemistry00silv_0/page/178.










