Convex combination




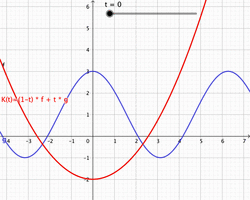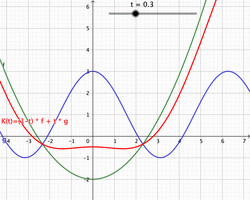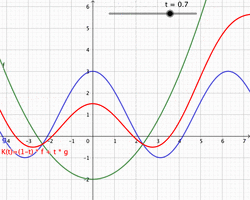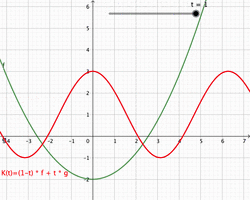
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1.[1] In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the count of the weights as in a standard weighted average.
More formally, given a finite number of points [math]\displaystyle{ x_1, x_2, \dots, x_n }[/math] in a real vector space, a convex combination of these points is a point of the form
- [math]\displaystyle{ \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n }[/math]
where the real numbers [math]\displaystyle{ \alpha_i }[/math] satisfy [math]\displaystyle{ \alpha_i\ge 0 }[/math] and [math]\displaystyle{ \alpha_1+\alpha_2+\cdots+\alpha_n=1. }[/math][1]
As a particular example, every convex combination of two points lies on the line segment between the points.[1]
A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical to the set of all their convex combinations.[1]
There exist subsets of a vector space that are not closed under linear combinations but are closed under convex combinations. For example, the interval [math]\displaystyle{ [0,1] }[/math] is convex but generates the real-number line under linear combinations. Another example is the convex set of probability distributions, as linear combinations preserve neither nonnegativity nor affinity (i.e., having total integral one).
Other objects
- A random variable [math]\displaystyle{ X }[/math] is said to have an [math]\displaystyle{ n }[/math]-component finite mixture distribution if its probability density function is a convex combination of [math]\displaystyle{ n }[/math] so-called component densities.
Related constructions
- A conical combination is a linear combination with nonnegative coefficients. When a point [math]\displaystyle{ x }[/math] is to be used as the reference origin for defining displacement vectors, then [math]\displaystyle{ x }[/math] is a convex combination of [math]\displaystyle{ n }[/math] points [math]\displaystyle{ x_1, x_2, \dots, x_n }[/math] if and only if the zero displacement is a non-trivial conical combination of their [math]\displaystyle{ n }[/math] respective displacement vectors relative to [math]\displaystyle{ x }[/math].
- Weighted means are functionally the same as convex combinations, but they use a different notation. The coefficients (weights) in a weighted mean are not required to sum to 1; instead the weighted linear combination is explicitly divided by the sum of the weights.
- Affine combinations are like convex combinations, but the coefficients are not required to be non-negative. Hence affine combinations are defined in vector spaces over any field.
See also
- Affine hull
- Carathéodory's theorem (convex hull)
- Simplex
- Barycentric coordinate system
- Convex space
References
External links
- Convex sum/combination with a trianglr - interaktive illustration
- Convex sum/combination with a hexagon - interaktive illustration
- Convex sum/combination with a tetraeder - interaktive illustration
de:Linearkombination#Konvexkombination
 |

