Poncelet–Steiner theorem

From HandWiki
Revision as of 18:33, 6 February 2024 by WikiGary (talk | contribs) (add)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Universality of construction using just a straightedge and a single circle with center
To draw the parallel (h) to a diameter g through any given point P. Chose auxiliary point C anywhere on the straight line through B and P outside of BP. (Steiner)

In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions having additional restrictions imposed on the traditional rules. This result states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given. This theorem is related to the rusty compass equivalence.

Any Euclidean construction, insofar as the given and required elements are points (or lines), if it can be completed with both the compass and the straightedge together, may be completed with the straightedge alone provided that no fewer than one circle with its center exist in the plane.

Though a compass can make constructions significantly easier, it is implied that there is no functional purpose of the compass once the first circle has been drawn. All constructions remain possible, though it is naturally understood that circles and their arcs cannot be drawn without the compass. This means only that the compass may be used for aesthetic purposes, rather than for the purposes of construction. All points that uniquely define a construction, which can be determined with the use of the compass, are equally determinable without, albeit with greater difficulty.

Constructions carried out in adherence with this theorem - relying solely on the use of a straightedge tool without the aid of a compass - are known as Steiner constructions. Steiner constructions may involve any number of circles, including none, already drawn in the plane, with or without their centers. They may involve all manner of unique shapes and curves preexisting in the plane, also, provided that the straightedge tool is the only physical tool at the geometers disposal. Whereas the Poncelet-Steiner theorem stipulates the existence of a circle and its center, and affirms that a single circle is equivalent to a compass.

History

"The geometrical constructions, carried out using the straight line and a fixed circle, as a subject of teaching at higher educational institutions and for practical use; by Jacob Steiner, Doctor of philosophy, Royal Prussian professor and distinguished teacher of mathematics at the commercial school in Berlin. With two copper plaques. Berlin, with Ferdinand Dummler. 1833."

In the tenth century, the Persian mathematician Abu al-Wafa' Buzjani (940−998) considered geometric constructions using a straightedge and a compass with a fixed opening, a so-called rusty compass. Constructions of this type appeared to have some practical significance as they were used by artists Leonardo da Vinci and Albrecht Dürer in Europe in the late fifteenth century. A new viewpoint developed in the mid sixteenth century when the size of the opening was considered fixed but arbitrary and the question of how many of Euclid's constructions could be obtained was paramount.[1]

Renaissance mathematician Lodovico Ferrari, a student of Gerolamo Cardano in a "mathematical challenge" against Niccolò Fontana Tartaglia was able to show that "all of Euclid" (that is, the straightedge and compass constructions in the first six books of Euclid's Elements) could be accomplished with a straightedge and rusty compass. Within ten years additional sets of solutions were obtained by Cardano, Tartaglia and Tartaglia's student Benedetti. During the next century these solutions were generally forgotten until, in 1673, Georg Mohr published (anonymously and in Dutch) Euclidis Curiosi containing his own solutions. Mohr had only heard about the existence of the earlier results and this led him to work on the problem.[2]

Showing that "all of Euclid" could be performed with straightedge and rusty compass is not the same as proving that all straightedge and compass constructions could be done with a straightedge and just a rusty compass. Such a proof would require the formalization of what a straightedge and compass could construct. This groundwork was provided by Jean Victor Poncelet in 1822, having been motivated by Mohr's work on the Mohr-Mascheroni theorem. He also conjectured and suggested a possible proof that a straightedge and rusty compass would be equivalent to a straightedge and compass, and moreover, the rusty compass need only be used once. The result that "a straightedge and single circle with given centre is equivalent to a straightedge and compass" was proved by Jakob Steiner in 1833.[3][1]

Relationships to other constructs

Various other notions, tools, terminology, etc., is often associated (sometimes loosely) to the Poncelet-Steiner theorem. Some are listed here.

Steiner constructions

The term Steiner construction typically refers to any geometric construction that utilizes the straightedge tool only, and is sometimes simply called a straightedge-only construction. No stipulations are made about what geometric objects already exist in the plane or their relative placement; any such conditions are postulated ahead of time. Also, no implications are made about what is or is not possible to construct.

Therefore, all constructions adhering to the Poncelet-Steiner theorem are Steiner constructions, though not all Steiner constructions abide by the condition of only one circle with its center provided in the plane. The Poncelet-Steiner theorem does not require an actual compass - it is presumed that the circle preexists in the plane - therefore all constructions herein demonstrating the Poncelet-Steiner theorem are Steiner constructions.

Rusty compass

The rusty compass describes a compass whose hinge is so rusted as to be fused such that its legs - the needle and pencil - are unable to adjust width. In essence, it is a compass whose distance is fixed, and which draws circles of a predetermined and constant, but arbitrary radius. Circles may be drawn centered at any arbitrary point, but the radius is unchangeable.

As a restricted construction paradigm, the rusty compass constructions allow the use of a straightedge and the fixed-width compass. The rusty compass equivalence:

All points necessary to uniquely describe any compass-straightedge construction may be achieved with a straightedge and fixed-width compass.

It is naturally understood that the arbitrary-radius compass may be used for aesthetic purposes; only the arc of the fixed-width compass may be used for construction.

In some sense, the rusty compass is a generalization and simplification of the Poncelet-Steiner theorem. Though not more powerful, it is certainly more convenient. The Poncelet-Steiner theorem requires a single circle with arbitrary radius and center point to be placed in the plane. As it is the only drawn circle, whether or not it was drawn by a rusty compass is immaterial and equivalent. The benefit of general rusty compass constructions, however, is that the compass may be used repeatedly to redraw circles centered at any desired point, albeit with the same radius, thus simplifying many constructions. Naturally if all constructions are possible with a single circle arbitrarily placed in the plane, then the same can surely be said about a straightedge and rusty compass, with which at least one circle may be arbitrarily placed.

It is known that a straightedge and a rusty compass is sufficient to construct all that is possible with straightedge and standard compass - with the implied understanding that circular arcs of arbitrary radii cannot be drawn, and only need be drawn for aesthetic purposes rather than constructive ones. Historically this was proven when the Poncelet-Steiner theorem was proven, which is a stronger result. The rusty compass, therefore, is no weaker than the Poncelet-Steiner theorem. The rusty compass is also no stronger.

The Poncelet-Steiner theorem reduces Ferrari's rusty compass equivalence, a claim at the time, to a single-use compass:

All points necessary to uniquely describe any compass-straightedge construction may be achieved with only a straightedge, once the first circle has been placed.

The Poncelet-Steiner theorem takes the rusty compass scenario, and breaks the compass completely after its first use.

Steiner's theorem

Not to be confused for Steiner's parallel axis theorem

If only one circle is to be given and no other special information, Steiner's theorem implies that the center of the circle must be provided along with the arc of the circle. This is done by proving the impossibility of constructing the circle's center from straightedge alone using only a single circle in the plane, without its center. An argument using projective transformations and Steiner's conic sections is used.

With only one circle provided in the plane, its center cannot be constructed by straightedge alone.

A naïve summary of the proof is as follows. With the use of a straightedge tool, only linear projective transformations are possible, and linear projective transformations are reversible operations. Lines project onto lines under any linear projective transformation, while conic sections project onto conic sections under a linear projective transformation, but the latter are skewed such that eccentricities, foci, and centers of circles are not preserved. Under different sequences of mappings, the center does not map uniquely and reversibly. This would not be the case if lines could be used to determine a circles center. As linear transformations are reversible operations and would thus produce unique results, the fact that unique results are not possible implies the impossibility of center-point constructions. The uniqueness of the constructed center would depend on additional information which makes the construction reversible.

Thus it is not possible to construct everything that can be constructed with straightedge and compass with straightedge alone. Consequently, requirements on the Poncelet-Steiner theorem cannot be weakened with respect to the circle center. If the centre of the only given circle is not provided, it cannot be obtained by a straightedge alone. Many constructions are impossible with straightedge alone. Something more is necessary, and a circle with its center identified is sufficient.

Alternative Frameworks to the Single Circle with Center

Alternatively, the center may be omitted with sufficient additional information. This is not a weakening of the Poncelet-Steiner theorem, merely an alternative framework. Nor is it a contradiction of Steiner's Theorem which hypothesizes only a single circle. The inclusion of this sufficient alternative information, which always includes at least two circles, disambiguates the mappings under the projective transformations, thus allowing various Steiner constructions to recover the circle center.

Each of these alternatives requires at least two circles devoid of their centers, plus some other unique piece of information. Some alternatives include two concentric or two intersecting circles, or three circles, or other variations wherein the provided circles are devoid of their centers. In each, some additional unique-but-sufficient criterion is met, such as concentricity, intersection points, a third circle, etc., respectively. In any of these cases, the center of a circle can be constructed, thereby reducing the problem to the Poncelet-Steiner theorem hypothesis (with the added convenience of having additional circles in the plane, all of whose centers may now be constructed).

Constructive proof approach

To prove the theorem, each of the basic constructions of compass and straightedge need to be proven to be possible by using a straightedge alone (provided that a circle and its center exist in the plane), as these are the foundations of, or elementary steps for, all other constructions. That is to say, all constructions can be written as a series of steps involving these five basic constructions:

  1. Creating the line through two existing points
  2. Creating the circle through one point with centre another point
  3. Creating the point which is the intersection of two existing, non-parallel lines
  4. Creating the one or two points in the intersection of a line and a circle (if they intersect)
  5. Creating the one or two points in the intersection of two circles (if they intersect).

#1 – A line through two points

This can be done with a straightedge alone. Neither a compass nor a circle is required.

#2 – A circle through one point with defined center

It is understood that the arc of a circle cannot be drawn without a compass. A circle is considered to be given by any two points, one defining the center and one existing on the circumference at radius. Any such pair define a unique circle, although the converse is not true: for any given circle there is no unique pair defining it. In keeping with the intent of the theorem which we aim to prove, the actual circle need not be drawn but for aesthetic reasons.

#3 – Intersection of two lines

This construction can also be done directly with a straightedge.

#4, #5 – Intersections involving the circle

Thus, to prove the theorem, only constructions #4 and #5 need be proven possible using only a straightedge and a given circle with its center.

Notes

Any doubts about constructions #1 or #3 would apply equally to the traditional construction paradigm involving the compass, and thus are not concerns unique to the Poncelet-Steiner theorem.

Construction #2 should not be of concern. Even though it is undisputed that a unique circle is defined by a center point and a point on its circumference, the pertinent question is whether or not this is sufficient information for the purposes of construction, or if the drawn arc is required. The arc of the circle is only used in traditional construction paradigms for the purposes of circle-circle and circle-line intersections, therein the arc of the circle is used directly to identify intersection points. Thus if constructions #4 and #5 are satisfiable without the arc of the circle with which to intersect, then it will prove the non-necessity of drawing the arc. This would therefore imply that construction #2 is satisfied by a simple labeling of two points, identifying the unique circle.

Constructive proof

In general constructions there are often several variations that will produce the same result. The choices made in such a variant can be made without loss of generality. However, when a construction is being used to prove that something can be done, it is not necessary to describe all these various choices and, for the sake of clarity of exposition, only one variant will be given below. The variants chosen below are done so for their ubiquity in application rather than their simplicity under any particular set of special conditions.

The constructive proof doesn't merely serve as a proof of the theorem, but also demonstrates the practical application of the most basic constructions, such that the claim of constructability with a straightedge could be employed in practice, in the most general case.

Note on Nomenclature

In the constructions below, a circle defined by a center point P and a point on its circumference, Q, through which the arc of the circle passes, is denoted P(Q). As most circles are not compass-drawn, center and circumference points are named explicitly. The arc may also be named. Per the theorem, when a compass-drawn circle is provided it is simply referred to as the given circle or the provided circle. The provided circle should always be assumed to be placed arbitrarily in the plane with an arbitrary radius (i.e. in general position).

Caveats

The intersection points between any line and the given circle may be found directly. The Poncelet-Steiner Theorem does not prohibit the normal treatment of circles already drawn in the plane; normal construction rules apply. The theorem only prohibits the construction of new circular arcs with a compass.

Steiner constructions and those constructions herein proving the Poncelet-Steiner theorem require the arbitrary placement of points in space. In some construction paradigms - such as in the geometric definition of the constructible number - this may be prohibited. With such a restriction against the placement of arbitrary points, the single circle may indeed be weaker than the compass.

Some preliminary constructions

To prove the above constructions #4 and #5, which are included below, a few necessary intermediary constructions are also explained below since they are used and referenced frequently. These are also straightedge-only constructions. All constructions below rely on basic constructions #1,#2,#3, and any other construction that is listed prior to it.

Parallel of a line having a colinear bisected segment

Construction of a parallel line through an arbitrary point, of a given arbitrary line having a bisected segment embedded.

This construction does not require the use of the given circle. Naturally any line that passes through the center of the given circle implicitly has a bisected segment: the diameter is bisected by the center. The animated GIF file embedded at the introduction to this article demonstrates this construction - relying on the bisected diameter; the arc of the circle is never used - which is reiterated here without the circle and with enumerated steps.

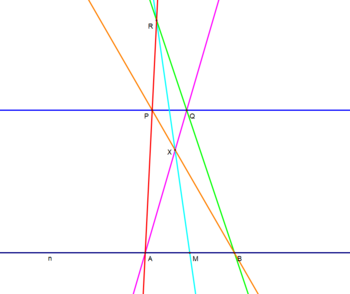
Given an arbitrary line n (in black) on which there exist two points A and B, having a midpoint M between them, and an arbitrary point P in the plane (assumed not to be on line n) through which a parallel of line n is to be made:

  1. Construct a line AP (in red).
  2. Construct a line BP (in orange).
  3. Define an arbitrary point R on line AP.
  4. Construct a line BR (in green).
  5. Construct a line MR (in light blue).
  6. Lines MR and BP intersect at point X.
  7. Construct a line AX (in purple).
  8. Lines BR and AX intersect at point Q.
  9. Construct a line PQ (in dark blue), the desired parallel.

In some literature the bisected line segment is sometimes viewed as a one-dimensional "circle" existing on the line. Alternatively, some literature views the bisected line segment as a two dimensional circle in three dimensional space with the line passing through a diameter, but not parallel to the plane, thus intersecting the plane of construction at two points on the circumference with the midpoint simply being the prescribed circle center.

This construction is a special case of the projective harmonic conjugate construction, which is not demonstrated in this article.

Creating a bisected segment on a line

If the line passes through the center of a circle, the segment defined by the diameter through the circle is bisected by the center of the circle. In the general case, however, any other line in the plane may have a bisected segment constructed onto it. This construction does require the use of the given circle.

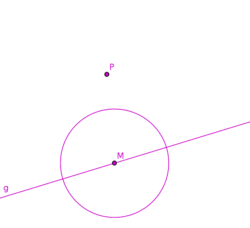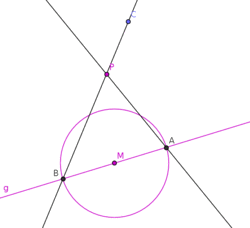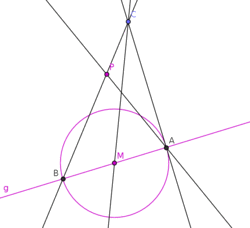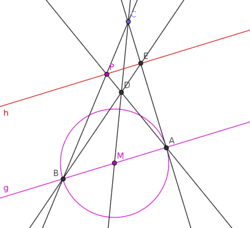
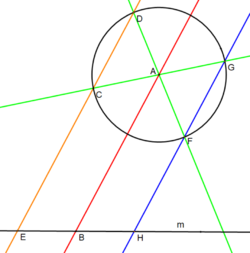
Construction of an arbitrary bisected line segment on a given line.

Given a line, m (in black), and a circle centered at A, we wish to create points E, B, and H on the line such that B is the midpoint:

  1. Draw an arbitrary line (in red) passing through the given circles center, A, and the desired midpoint B (chosen arbitrarily) on the line m.
    • Notice that the red line, AB, passes through the center of the circle and highlights a diameter, bisected by the circle center. Any parallel may be made from this line according to the previous construction.
  2. Choose an arbitrary point C on the given circle
    • For convenience the point should not lie on the perpendicular of line AB through the circle center.
  3. Construct a line (in orange), passing through C, that is parallel to the red line AB.
    • If point C is on the perpendicular of AB through the circle center, the parallel would be a tangent to the circle. The construction is possible by other means not listed in this article, but it is also unnecessary to choose such a point.
    • This parallel intersects the given circle at D.
    • This parallel also intersects the black line m at E, defining one end of the line segment.
  4. Create two lines (in green), AC and AD, that each pass through the given circles center.
    • These green lines intersect the given circle at points G and F, respectively.
  5. Line FG (in blue) intersects the line m at H, defining the other endpoint of the line segment.
    • Segment EH now exists coincident with line m and having midpoint B.

As point C is chosen arbitrarily, there is no need for it to inconveniently be on the perpendicular of line AB through the circle center. If however it is, line CD is merely the tangent line to the circle through point C, which is coincident to point D. This construction is possible though the construction is not listed in this article. Points F and G may be constructed as before, and will also equal one another. And again, line GF is merely the tangent line to the circle at that point. Thus points E, H and their midpoint B may be found, as before, with only a minor change adding a subconstruction.

Constructing a parallel of any line

This construction does require the use of the given circle. In order to generalize the parallel line construction to all possible lines, not just the ones with a collinear bisected line segment, it becomes necessary to have additional information. In keeping with the Poncelet-Steiner theorem, a circle (with center) is the object of choice for this construction.

To construct a parallel line of any given line, through any point in the plane, we trivially combine two constructions:

  1. Any line from which a parallel is to be made must have a bisected segment constructed onto it, if one does not already exist.
  2. A parallel is then constructed according to the previous parallel construction involving the collinear bisected segment.

In alternative constructions, which are not demonstrated in this article, a parallel may be constructed from any pair of lines which are already parallel to one another; thus a third parallel may be produced from any two, without the use of a circle. Additionally, a parallel of any line may be constructed whenever there exists in the plane any parallelogram, also without the use of a given circle.

Constructing a perpendicular line

Construction of a perpendicular line.

This construction does require the use of the given circle and takes advantage of Thales's theorem.

From a given line m, and a given point A in the plane, a perpendicular to the line is to be constructed through the point. Provided is the given circle O(r).

  1. If the desired line from which a perpendicular is to be made, m, does not pass through the given circle - as is depicted - or it also passes through the given circle's center, then a new parallel line (in red) may be constructed arbitrarily such that it does pass through the given circle but not its center, and the perpendicular is to be made from this line instead.
  2. This red line which passes through the given circle but not its center, will intersect the given circle in two points, B and C.
  3. Draw a line BO (in orange), through the circle center.
    • This line intersects the given circle at point D.
  4. Draw a line DC (in light green).
    • This line is perpendicular to the red (and therefore the black) lines, BC and m.
  5. Construct a parallel of line DC through point A using previous constructions.
    • A perpendicular of the original black line, m, now exists in the plane, line DC.
    • A parallel of any line may be constructed through any point in the plane.

If the line from which a perpendicular is to be made does pass through the circle center, an alternative approach would be to construct the tangent lines to the circle at the lines points of intersection, using Steiner constructions. This is not demonstrated in this article.

Another option in the event the line passes through the circles center would be to construct a parallel to it through the circle at an arbitrary point. An isosceles trapezoid (or potentially an isosceles triangle) is formed by the intersection points to the circle of both lines. The two non-parallel sides of which may be extended to an intersection point between them, and a line drawn from there through the circle's center. This line is perpendicular, and the diameter is bisected by the center.

By an alternative construction not demonstrated in this article, a perpendicular of any line may be constructed without a circle, provided there exists in the plane any square.

Constructing the midpoint of any segment (segment bisection)

Construction of the midpoint of an arbitrary line segment from a non-collinear parallel line.

Given is a line segment AB, which is to be bisected. Optionally, a parallel line m exists in the plane.

  1. If the line m, which is parallel to line segment AB, does not exist in the plane then it must be constructed according to earlier constructions using the given circle in the plane (not depicted).
    • A given circle in the plane is not required for this construction if the parallel already exists.
    • The parallel may be placed in the plane arbitrarily, so long as it is not collinear with the line segment.
  2. Arbitrarily choose a point C in the plane which is not collinear with the line or the line segment.
    • One may, alternatively, construct point C as the intersection of lines AD and BE, provided that points D and E already exist on a parallel line m.
  3. Draw a line AC (in red), intersecting line m at point D.
  4. Draw a line BC (in orange), intersecting line m at point E.
  5. Draw two lines, AE and BD (each in light green), intersecting each other at point X
  6. Draw a line CX (in blue), intersecting segment AB at point M.
    • Point M is the desired midpoint of segment AB.
    • Line CX also bisects segment DE

For added perspective, in some sense this construction is a variant of a previous construction of a parallel from a bisected line segment, and is therefore also a special case of the projective harmonic conjugate (not provided in this article). It is the same set of lines when taken on whole, but constructed in a different order, and from a different initial set of conditions, arriving at a different end goal.

Since any arbitrary segment on one of two parallel lines can be bisected, and any line with a bisected segment on it may have a parallel constructed, the two scenarios are geometrically equivalent propositions. They imply one another; a simple construction can convert one scenario into the other using no additional information.

In an alternative construction, any line segment may be bisected whenever a parallelogram exists in the plane.

Rotating a line segment

To define a circle only the center and one point - any point - on the circumference is required. In principle a new point B' is constructed such that circle A(B) is equal to circle A(B'), though the point B is not equal to point B' . In essence, segment AB is rotated about the axis point A, to AB' , for a different set of defining points for the same circle.

Steiner construction of the rotation of a line segment

One way of going about this which satisfies most conditions is as follows:

  1. Draw the line segment AB (in black).
  2. Construct a parallel (in red) of line AB through the center, point O, of the given circle.
    • The parallel intersects the given circle at some point b.
  3. Choose a point b' arbitrarily on the given circle not colinear with line Ob.
  4. Draw a line Ob' (in orange).
  5. Construct a parallel line to Ob' through point A (in pink).
  6. Draw a line bb' (in light green), connecting the points on the circles circumference.
  7. Construct a parallel of line bb' through point B (in blue).
  8. Intersect the blue and pink parallels, from points B and A, respectively.
    • This is point B' .
    • Point B' is the desired point, rotating the line segment and defining the same circle centered at A.

This construction will fail if the desired rotation is diametrically opposite the circle (i.e. a half-circle rotation). One solution to this scenario is to employ two separate rotation constructions, neither one a half-circle rotation from the previous, one acting as an intermediary step. Choose any rotation angle arbitrarily, complete the rotation, then choose the supplemental angle and perform the rotation a second time.

There does exist a second, alternative rotation construction solution, based on projections and perspective points. Though it avoids the aforementioned half-circle rotation complication, it does have its own complications, which are similarly resolved with intermediary rotation constructions. The construction is no more versatile. It is not demonstrated in this article.

Constructing the radical axis between circles

Straightedge-only construction of the radical axis between circles.

This construction does require the use of the given circle (which is not depicted) for the referenced sub-constructions previously demonstrated.

Suppose two circles A(B) and C(D) are implicitly given, defined only by the points A, B, C, and D in the plane, with their centers defined, but are not compass-constructed. The radical axis, line m (in dark blue), between the two circles may be constructed:

  1. Draw a line AC (in orange) through the circle centers.
  2. Draw a line segment BD (in red) between the points on the circumference of the circles.
  3. Find the midpoint, M, of segment BD.
  4. Draw lines AM and CM (both in light green), connecting the segment midpoint with each of the circle centers.
  5. Construct a line j (in purple) passing through point B, and perpendicular to AM.
    • Line j is the radical axes between circle M(B) and circle A(B).
  6. Construct a line k (in dark green) passing through point D, and perpendicular to CM.
    • Line k is the radical axes between circle M(B) and circle C(D).
  7. Lines j and k intersect at point X.
    • If the lines j and k are parallel then the segment midpoint M is on the line AC - the centers of circles A(B), C(D), and M(B) are colinear - and the construction will fail. An alternative approach is required (see below).
    • Point X is the power center between circles A(B), C(D), and M(B), and therefore is the unique point that lies on the radical axis between any two of the three circles.
  8. Construct a line m (in dark blue) perpendicular to line AC and passing through point X.
    • Line m is the desired radical axis.

In the event that the construction of the radical axis fails due to there not being an intersection point X between parallel lines j and k, which results from the coincidental placement of the midpoint M on the line AC, an alternative approach is required. One such approach is to rotate the segment AB about the axis point A (the center of circle A(B)). Once arrived at the arbitrary rotation AB' , which defines the same circle, the radical axis construction can begin anew without issue.

Intersecting a line with a circle (Construction #4)

The straightedge-only construction of the intersection points between a line and a circle.

This construction does require the use of the provided circle, O(r). Any line may be naturally intersected with any compass-drawn circle.

Given is the line m (in black) and the circle P(Q), which is not compass-constructed. The intersection points of the circle P(Q) and the line m, which are point A and B, may be constructed:

  1. Draw a line PQ (in red) through the points defining the circle.
    • If point O is colinear with line PQ then segment PQ will need to be rotated about the center point P of the circle, and this construction restarted anew.
  2. Construct a parallel (in orange) of line PQ through the center O of the provided circle.
    • The parallel intersects the provided circle at two points, one of which is arbitrarily chosen: R.
  3. Draw a line PO (in light green), through the centers of the two circles (i.e. the one provided by compass construction and the one which is to be intersected).
  4. Draw a line QR (in light blue), connecting the two points on the circumferences of the two circles.
  5. Intersect the lines PO and QR at point X.
    • If point X does not exist due to lines PO and QR being parallel - which results from circles P(Q) and O(r) having equal radii - then refer back to step 2 and choose the alternate point of intersection, R.
  6. Choosing a point M arbitrarily on line m, such that it is not on line PO, draw a line PM (in pink).
    • For construction simplicity and only if line PQ is not parallel to line m, lines PM and PQ may be coincident.
  7. Draw a line MX (in brown).
  8. Construct a parallel (in dark purple) of line PM through the center O of the provided circle.
    • The parallel intersects the line MX at a point N.
  9. Construct a parallel (in yellow) of line m through the point N.
    • The parallel intersects the provided circle at points C and D.
    • If the parallel does not intersect the provided circle then neither does the line m intersect circle P(Q).
  10. Draw lines CX and DX (both in dark blue).
    • These lines both intersect line m at points A and B, respectively.
  11. Points A and B are the desired points of intersection between the line m and the circle P(Q).

Intersecting two circles (Construction #5)

The intersection between two circles becomes a trivial combination of two earlier constructions:

  1. Construct the radical axis between the two circles.
  2. Construct the intersection points between the radical axis and either one of the two circles arbitrarily chosen:
    • The radical axis is a line, so this construction is possible per the previous construction: basic construction #4.
  3. These points are the desired points of intersection of the circles.
    • The two circles and the radical axis all intersect at the same loci of points: two points, one point if tangential, or none if they do not intersect.
    • If the radical axis does not intersect one circle then it intersects neither, and neither do the two circles intersect.

A circle through one point centered at another point (Construction #2, revisited)

The second basic construction - describing a full circle with just two defining points - never needed an arc to be constructed with the compass in order for the circle to be utilized in constructions. Namely, the intersections of circles both with circles and with lines, which together are the essence of all constructions involving a circle, are achievable without the arc. Thus defining a circle by its center and by any arbitrary point on its circumference is sufficient to fully describe the entire circle and construct with it. As such, the arc only serves an aesthetic purpose. Basic construction #2 is satisfied.

Conclusion

Since all five basic constructions have been shown to be achievable with only a straightedge, provided that a single circle with its center is placed in the plane, this proves the Poncelet-Steiner theorem.

Projective Geometry and the Poncelet-Steiner Theorem

Further information: Projective geometry

Though a distinct topic in its own right, many of the concepts of projective geometry are applied here to Steiner constructions. Jean-Victor Poncelet was a major contributor to the subject when he postulated the theorem of this article, which Jakob Steiner later proved. Many of the related concepts developed in projective geometry include but are not limited to: concurrence, "points at infinity", perspective, ratios and cross ratios, stable or fixed points of involutions, invariants, homogeneity, linear transformations, projective harmonics, and others. A thorough treatment of Steiner constructions and their proofs require a background in projective geometry, though the subject of projective geometry is not restricted to straightedge-only constructions.

Other types of restricted construction

Restricted constructions involving the compass

The Poncelet–Steiner theorem can be contrasted with the Mohr–Mascheroni theorem, which states that any compass and straightedge construction can be performed with only a compass. The straightedge is not required but for aesthetic purposes; nothing else is needed in the plane.

The rusty compass restriction allows the use of a compass and straightedge, provided that the compass produces circles of fixed radius. Although the rusty compass constructions were explored since the 10th century, and all of Euclid was shown to be constructable with a rusty compass by the 17th century, the Poncelet-Steiner theorem proves that the rusty compass and straightedge together are more than sufficient for any and all Euclidean construction. Indeed, the rusty compass becomes a tool simplifying constructions over merely the straightedge and single circle. Viewed the other way, the Poncelet-Steiner theorem not only fixes the width of the rusty compass, but ensures that the compass breaks after its first use.

The compass equivalence theorem proves that the rigid compass (also called the modern compass) - one that holds its spacing when lifted from the plane - is equivalent to the traditional collapsing compass (also called divider) - one that does not retain its spacing, thus "resetting to zero", every time it is lifted from the plane. The ability to transfer distances (i.e. construct congruent circles) - an operation made trivial by the rigid compass - was proven by Euclid to be possible with the collapsing compass. In fact it can be done using only the collapsing compass, without the straightedge tool. Consequently the rigid compass and collapsing compasses are equivalent; what can be constructed by one can be constructed by the other.

Restricted Steiner constructions

The requirement placed on the Poncelet-Steiner theorem - that one circle with its center provided exist in the plane - has been since generalized, or strengthened, to include alternative but equally restrictive conditions.

Other unique scenarios undoubtedly exist than those listed here. This is not an exhaustive list of possibilities.

Poncelet-Steiner without the full circular arc

In one such alternative, the entire circle is not required at all. In 1904, Francesco Severi proved that any small arc (of the circle), together with the centre, will suffice.[4] This construction breaks the rusty compass at any point before the first circle is completed, but after it has begun, thus drawing some continuous portion of the arc of the circle in the plane, and still all constructions remain possible. Thus, the conditions hypothesizing the Poncelet-Steiner theorem may indeed be weakened, but only with respect to the completeness of the circular arc, and not, per the Steiner theorem, with respect to the center.

The theorem demonstrates the Steiner construction of the intersection points between a line and the circle of an arc, regardless of the size or position of the arc, using only a straightedge and the arc. The construction, also, does not make use of the center of the circle of the arc. Though the center is required to complete all of Euclid, as the Steiner theorem and the Poncelet-Steiner theorem both proves, the center is not needed in order to intersect a line with the circle of that arc. Using this construction, the arc, and the center of the circle of the arc, all of the above Poncelet-Steiner constructions are equally achievable, albeit with greater difficulty.

Poncelet-Steiner without the circle center

In two other alternatives, the centre may be omitted entirely provided that given are either two concentric circles, or two distinct intersecting circles, of which there are two cases: two intersection points and one intersection point (tangential circles). From any of these scenarios, centres can be constructed, reducing the scenario to the original hypothesis. These do not contradict Steiner's theorem which, although stating a center is absolutely required, also hypothesizes only one circle exists.

Still other variations exist. It suffices to have two non-intersecting, non-concentric circles (without their centres), provided that at least one point is given on either the centerline through them or on the radical axis between them, or provided any two parallel lines arbitrarily in the plane. It also suffices, alternatively, to have three non-intersecting circles.[5] Once a single center is constructed, the scenario again reduces to the original hypothesis of the Poncelet-Steiner theorem.

In each of these scenarios, more information exists than just a second circle. The fact that two circles are concentric, or that two circles have known intersection points, or the presence of a third circle, or of a point on either a centerline or a radical axis, constitutes an additional piece of information beyond merely the presence of a second circle.

Also in each of the previously mentioned scenarios, the completeness of the circular arc is not necessary, as per Severi's 1904 theorem, provided that circle intersections are explicitly given whenever arcs of the circle(s) do not exist where intersection points do. That is, if intersection points cannot be found directly by way of the two arcs, they must be provided. The completeness of the circular arc is otherwise redundant.

Extended, liberated, or neusis, constructions

Instead of restricting the rules of construction further, it is of equal interest to study relaxing the restrictions. These are sometimes called extended constructions, because they extend what is constructible by extending the allowable toolset. These constructions are also called neusis constructions (from Greek) because they employ tools other than the compass and straightedge, or liberated constructions because they alleviate the restrictions of the traditional paradigm.

Just as geometers have studied what remains possible to construct (and how) when additional restrictions are placed on traditional construction rules - such as compass only, straightedge only, rusty compass, etc. - they have also studied what constructions becomes possible that weren't already when the natural restrictions inherent to traditional construction rules are alleviated. Questions such as "what becomes constructible", "how might it be constructed", "what are the fewest traditional rules to be broken", "what are the simplest tools needed", "which seemingly different tools are equivalent", etc. are asked.

The arbitrary angle is not trisectable using traditional compass and straightedge rules, for example, but the trisection becomes constructible when allowed the additional tool of an ellipse in the plane, which is itself not constructible. Some of the traditional unsolved problems such as angle trisection, doubling the cube, squaring the circle, finding cubic roots, etc., since proven to be impossible by straightedge and compass alone, have been resolved using an expanded set of tools. In general, the objects studied to extend the scope of what is constructible have included:

  • Non-constructible "auxiliary" curves in the plane - including any of the conic sections, cycloids, lemniscates, limaçons, the Archimedean spiral, Euler spiral, any of the trisectrices or quadratrices, and others.
  • Physical tools other than the compass and straightedge - generally called neuseis - which include specific tools such as the Tomahawk, markable and double-edged straightedges, graduated rulers, right triangular rulers, linkages, ellipsographs, French curves, and others.
  • Paper-folding techniques, derived from the mathematical and geometric study of Origami.

The ancient geometers considered the compass and straightedge constructions (known as planar constructions) as ideal and preferred. Second to that they preferred solid constructions, which included the use of conic sections in the plane other than the circle. They favored thirdly the use of arbitrary smooth curves in the plane, and least of all the use of neuseis (alternative physical handheld tools). It is doubtful that the ancient geometers - at least of the western world - even considered paper folding.

The term neusis or neusis construction may also refer to a specific tool or method employed by the ancient geometers.

Approximations

It is worthwhile to point out that in all construction paradigms, the implicit rule is that all constructions must terminate in a finite number of applications of the available tools (compass and straightedge), and produce the exact intended results. Entire discussions could be made with either of these conditions alleviated.

For any otherwise non-constructible figure:

  • It is possible to approximate a construction to a predetermined level of accuracy using only compass and straightedge, using a reiterative approach.
  • Exact construction may become possible at the infinite limit of this convergent process, but requires infinite constructions.

For example, an angle trisection may be performed exactly using an infinite sequence of angle bisections. If the construction is terminated at some finite iteration, an accurate approximation of a trisection can be achieved to arbitrary accuracy. Although each point, line or circle is a valid construction, what it aims to approximate can never truly be achieved.

There are, of course, exactly constructible figures that are reasonable approximations for non-constructible figures, such as relatively simple non-iterative constructions for an approximation of the heptagon.

See also

Notes

  1. ↑ 1.0 1.1 Eves 1963, p.205
  2. ↑ Retz & Keihn 1989, p.195
  3. ↑ (in german) Die geometrischen Konstructionen, ausgeführt mittelst der geraden Linie und eines festen Kreises, als Lehrgegenstand auf höheren Unterrichts-Anstalten und zur praktischen Benutzung. Berlin: Ferdinand Dümmler. 1833. https://archive.org/details/bub_gb_xHc1T1W-ZXUC. Retrieved 2 April 2013. 
  4. ↑ Retz & Keihn 1989, p. 196
  5. ↑ Wolfram's Math World

References

  • Eves, Howard (1963), A Survey of Geometry /Volume one, Allyn and Bacon 
  • Retz, Merlyn; Keihn, Meta Darlene (1989), "Compass and Straightedge Constructions", Historical Topics for the Mathematics Classroom, National Council of Teachers of Mathematics (NCTM), pp. 192–196, ISBN 9780873532815 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Poncelet–Steiner_theorem&oldid=3372531"