Constructible number
In geometry and algebra, a real number [math]\displaystyle{ r }[/math] is constructible if and only if, given a line segment of unit length, a line segment of length [math]\displaystyle{ |r| }[/math] can be constructed with compass and straightedge in a finite number of steps. Equivalently, [math]\displaystyle{ r }[/math] is constructible if and only if there is a closed-form expression for [math]\displaystyle{ r }[/math] using only integers and the operations for addition, subtraction, multiplication, division, and square roots.
The geometric definition of constructible numbers motivates a corresponding definition of constructible points, which can again be described either geometrically or algebraically. A point is constructible if it can be produced as one of the points of a compass and straight edge construction (an endpoint of a line segment or crossing point of two lines or circles), starting from a given unit length segment. Alternatively and equivalently, taking the two endpoints of the given segment to be the points (0, 0) and (1, 0) of a Cartesian coordinate system, a point is constructible if and only if its Cartesian coordinates are both constructible numbers.[1] Constructible numbers and points have also been called ruler and compass numbers and ruler and compass points, to distinguish them from numbers and points that may be constructed using other processes.[2]
The set of constructible numbers forms a field: applying any of the four basic arithmetic operations to members of this set produces another constructible number. This field is a field extension of the rational numbers and in turn is contained in the field of algebraic numbers.[3] It is the Euclidean closure of the rational numbers, the smallest field extension of the rationals that includes the square roots of all of its positive numbers.[4]
The proof of the equivalence between the algebraic and geometric definitions of constructible numbers has the effect of transforming geometric questions about compass and straightedge constructions into algebra, including several famous problems from ancient Greek mathematics. The algebraic formulation of these questions led to proofs that their solutions are not constructible, after the geometric formulation of the same problems previously defied centuries of attack.
Geometric definitions
Geometrically constructible points
Let [math]\displaystyle{ O }[/math] and [math]\displaystyle{ A }[/math] be two given distinct points in the Euclidean plane, and define [math]\displaystyle{ S }[/math] to be the set of points that can be constructed with compass and straightedge starting with [math]\displaystyle{ O }[/math] and [math]\displaystyle{ A }[/math]. Then the points of [math]\displaystyle{ S }[/math] are called constructible points. [math]\displaystyle{ O }[/math] and [math]\displaystyle{ A }[/math] are, by definition, elements of [math]\displaystyle{ S }[/math]. To more precisely describe the remaining elements of [math]\displaystyle{ S }[/math], make the following two definitions:[5]
- a line segment whose endpoints are in [math]\displaystyle{ S }[/math] is called a constructed segment, and
- a circle whose center is in [math]\displaystyle{ S }[/math] and which passes through a point of [math]\displaystyle{ S }[/math] (alternatively, whose radius is the distance between some pair of distinct points of [math]\displaystyle{ S }[/math]) is called a constructed circle.
Then, the points of [math]\displaystyle{ S }[/math], besides [math]\displaystyle{ O }[/math] and [math]\displaystyle{ A }[/math] are:[5][6]
- the intersection of two non-parallel constructed segments, or lines through constructed segments,
- the intersection points of a constructed circle and a constructed segment, or line through a constructed segment, or
- the intersection points of two distinct constructed circles.
As an example, the midpoint of constructed segment [math]\displaystyle{ OA }[/math] is a constructible point. One construction for it is to construct two circles with [math]\displaystyle{ OA }[/math] as radius, and the line through the two crossing points of these two circles. Then the midpoint of segment [math]\displaystyle{ OA }[/math] is the point where this segment is crossed by the constructed line.[7]
Geometrically constructible numbers
The starting information for the geometric formulation can be used to define a Cartesian coordinate system in which the point [math]\displaystyle{ O }[/math] is associated to the origin having coordinates [math]\displaystyle{ (0,0) }[/math] and in which the point [math]\displaystyle{ A }[/math] is associated with the coordinates [math]\displaystyle{ (1, 0) }[/math]. The points of [math]\displaystyle{ S }[/math] may now be used to link the geometry and algebra by defining a constructible number to be a coordinate of a constructible point.[8]
Equivalent definitions are that a constructible number is the [math]\displaystyle{ x }[/math]-coordinate of a constructible point [math]\displaystyle{ (x,0) }[/math][6] or the length of a constructible line segment.[9] In one direction of this equivalence, if a constructible point has coordinates [math]\displaystyle{ (x,y) }[/math], then the point [math]\displaystyle{ (x,0) }[/math] can be constructed as its perpendicular projection onto the [math]\displaystyle{ x }[/math]-axis, and the segment from the origin to this point has length [math]\displaystyle{ x }[/math]. In the reverse direction, if [math]\displaystyle{ x }[/math] is the length of a constructible line segment, then intersecting the [math]\displaystyle{ x }[/math]-axis with a circle centered at [math]\displaystyle{ O }[/math] with radius [math]\displaystyle{ x }[/math] gives the point [math]\displaystyle{ (x,0) }[/math]. It follows from this equivalence that every point whose Cartesian coordinates are geometrically constructible numbers is itself a geometrically constructible point. For, when [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are geometrically constructible numbers, point [math]\displaystyle{ (x,y) }[/math] can be constructed as the intersection of lines through [math]\displaystyle{ (x,0) }[/math] and [math]\displaystyle{ (0,y) }[/math], perpendicular to the coordinate axes.[10]
Algebraic definitions
Algebraically constructible numbers
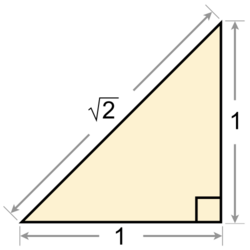
The algebraically constructible real numbers are the subset of the real numbers that can be described by formulas that combine integers using the operations of addition, subtraction, multiplication, multiplicative inverse, and square roots of positive numbers. Even more simply, at the expense of making these formulas longer, the integers in these formulas can be restricted to be only 0 and 1.[11] For instance, the square root of 2 is constructible, because it can be described by the formulas [math]\displaystyle{ \sqrt2 }[/math] or [math]\displaystyle{ \sqrt{1+1} }[/math].
Analogously, the algebraically constructible complex numbers are the subset of complex numbers that have formulas of the same type, using a more general version of the square root that is not restricted to positive numbers but can instead take arbitrary complex numbers as its argument, and produces the principal square root of its argument. Alternatively, the same system of complex numbers may be defined as the complex numbers whose real and imaginary parts are both constructible real numbers.[12] For instance, the complex number [math]\displaystyle{ i }[/math] has the formulas [math]\displaystyle{ \sqrt{-1} }[/math] or [math]\displaystyle{ \sqrt{0-1} }[/math], and its real and imaginary parts are the constructible numbers 0 and 1 respectively.
These two definitions of the constructible complex numbers are equivalent.[13] In one direction, if [math]\displaystyle{ q=x+iy }[/math] is a complex number whose real part [math]\displaystyle{ x }[/math] and imaginary part [math]\displaystyle{ y }[/math] are both constructible real numbers, then replacing [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] by their formulas within the larger formula [math]\displaystyle{ x+y\sqrt{-1} }[/math] produces a formula for [math]\displaystyle{ q }[/math] as a complex number. In the other direction, any formula for an algebraically constructible complex number can be transformed into formulas for its real and imaginary parts, by recursively expanding each operation in the formula into operations on the real and imaginary parts of its arguments, using the expansions[14]
- [math]\displaystyle{ (a+ib)\pm (c+id)=(a \pm c)+i(b \pm d) }[/math]
- [math]\displaystyle{ (a+ib)(c+id)=(ac-bd) + i(ad+bc) }[/math]
- [math]\displaystyle{ \frac{1}{a+ib}=\frac{a}{a^2+b^2} + i \frac{-b}{a^2+b^2} }[/math]
- [math]\displaystyle{ \sqrt{a+ib} = \frac{(a+r)\sqrt{r}}{s} + i\frac{b\sqrt{r}}{s} }[/math], where [math]\displaystyle{ r=\sqrt{a^2+b^2{}_{\!}} }[/math] and [math]\displaystyle{ s=\sqrt{(a+r)^2+b^2} }[/math].
Algebraically constructible points
The algebraically constructible points may be defined as the points whose two real Cartesian coordinates are both algebraically constructible real numbers. Alternatively, they may be defined as the points in the complex plane given by algebraically constructible complex numbers. By the equivalence between the two definitions for algebraically constructible complex numbers, these two definitions of algebraically constructible points are also equivalent.[13]
Equivalence of algebraic and geometric definitions
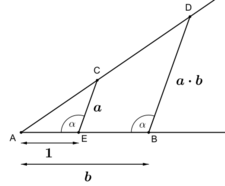
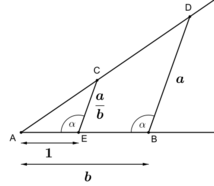
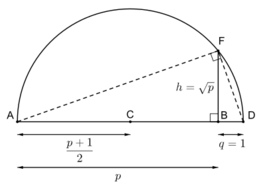
If [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are the non-zero lengths of geometrically constructed segments then elementary compass and straightedge constructions can be used to obtain constructed segments of lengths [math]\displaystyle{ a+b }[/math], [math]\displaystyle{ |a-b| }[/math], [math]\displaystyle{ ab }[/math], and [math]\displaystyle{ a/b }[/math]. The latter two can be done with a construction based on the intercept theorem. A slightly less elementary construction using these tools is based on the geometric mean theorem and will construct a segment of length [math]\displaystyle{ \sqrt{a} }[/math] from a constructed segment of length [math]\displaystyle{ a }[/math]. It follows that every algebraically constructible number is geometrically constructible, by using these techniques to translate a formula for the number into a construction for the number.[15]
In the other direction, a set of geometric objects may be specified by algebraically constructible real numbers: coordinates for points, slope and [math]\displaystyle{ y }[/math]-intercept for lines, and center and radius for circles. It is possible (but tedious) to develop formulas in terms of these values, using only arithmetic and square roots, for each additional object that might be added in a single step of a compass-and-straightedge construction. It follows from these formulas that every geometrically constructible number is algebraically constructible.[16]
Algebraic properties
The definition of algebraically constructible numbers includes the sum, difference, product, and multiplicative inverse of any of these numbers, the same operations that define a field in abstract algebra. Thus, the constructible numbers (defined in any of the above ways) form a field. More specifically, the constructible real numbers form a Euclidean field, an ordered field containing a square root of each of its positive elements.[17] Examining the properties of this field and its subfields leads to necessary conditions on a number to be constructible, that can be used to show that specific numbers arising in classical geometric construction problems are not constructible.
It is convenient to consider, in place of the whole field of constructible numbers, the subfield [math]\displaystyle{ \mathbb{Q}(\gamma) }[/math] generated by any given constructible number [math]\displaystyle{ \gamma }[/math], and to use the algebraic construction of [math]\displaystyle{ \gamma }[/math] to decompose this field. If [math]\displaystyle{ \gamma }[/math] is a constructible real number, then the values occurring within a formula constructing it can be used to produce a finite sequence of real numbers [math]\displaystyle{ \alpha_1,\dots, a_n=\gamma }[/math] such that, for each [math]\displaystyle{ i }[/math], [math]\displaystyle{ \mathbb{Q}(\alpha_1,\dots,a_i) }[/math] is an extension of [math]\displaystyle{ \mathbb{Q}(\alpha_1,\dots,a_{i-1}) }[/math] of degree 2.[18] Using slightly different terminology, a real number is constructible if and only if it lies in a field at the top of a finite tower of real quadratic extensions, [math]\displaystyle{ \mathbb{Q} = K_0 \subseteq K_1 \subseteq \dots \subseteq K_n, }[/math] starting with the rational field [math]\displaystyle{ \mathbb{Q} }[/math] where [math]\displaystyle{ \gamma }[/math] is in [math]\displaystyle{ K_n }[/math] and for all [math]\displaystyle{ 0\lt j\le n }[/math], [math]\displaystyle{ [K_j:K_{j-1}]=2 }[/math].[19] It follows from this decomposition that the degree of the field extension [math]\displaystyle{ [\mathbb{Q}(\gamma):\mathbb{Q}] }[/math] is [math]\displaystyle{ 2^r }[/math], where [math]\displaystyle{ r }[/math] counts the number of quadratic extension steps.[20]
Analogously to the real case, a complex number is constructible if and only if it lies in a field at the top of a finite tower of complex quadratic extensions.[21] More precisely, [math]\displaystyle{ \gamma }[/math] is constructible if and only if there exists a tower of fields [math]\displaystyle{ \mathbb{Q} = F_0 \subseteq F_1 \subseteq \dots \subseteq F_n, }[/math] where [math]\displaystyle{ \gamma }[/math] is in [math]\displaystyle{ F_n }[/math], and for all [math]\displaystyle{ 0\lt j\le n }[/math], [math]\displaystyle{ [F_j:F_{j-1}]= 2 }[/math]. The difference between this characterization and that of the real constructible numbers is only that the fields in this tower are not restricted to being real. Consequently, if a complex number [math]\displaystyle{ \gamma }[/math] is constructible, then [math]\displaystyle{ [\mathbb{Q}(\gamma):\mathbb{Q}] }[/math] is a power of two. However, this necessary condition is not sufficient: there exist field extensions whose degree is a power of two that cannot be factored into a sequence of quadratic extensions.[22]
The fields that can be generated in this way from towers of quadratic extensions of [math]\displaystyle{ \mathbb{Q} }[/math] are called iterated quadratic extensions of [math]\displaystyle{ \mathbb{Q} }[/math]. The fields of real and complex constructible numbers are the unions of all real or complex iterated quadratic extensions of [math]\displaystyle{ \mathbb{Q} }[/math].[23]
Trigonometric numbers
Trigonometric numbers are the cosines or sines of angles that are rational multiples of [math]\displaystyle{ \pi }[/math]. These numbers are always algebraic, but they may not be constructible. The cosine or sine of the angle [math]\displaystyle{ 2\pi/n }[/math] is constructible only for certain special numbers [math]\displaystyle{ n }[/math]:[24]
- The powers of two
- The Fermat primes, prime numbers that are one plus a power of two
- The products of powers of two and any number of distinct Fermat primes.
Thus, for example, [math]\displaystyle{ \cos(\pi/15) }[/math] is constructible because 15 is the product of the Fermat primes 3 and 5; but [math]\displaystyle{ \cos(\pi/9) }[/math] is not constructible (not being the product of distinct Fermat primes) and neither is [math]\displaystyle{ \cos(\pi/7) }[/math] (being a non-Fermat prime).
Impossible constructions
The Ancient Greece thought that certain problems of straightedge and compass construction they could not solve were simply obstinate, not unsolvable.[25] However, the non-constructibility of certain numbers proves that these constructions are logically impossible to perform.[26] (The problems themselves, however, are solvable using methods that go beyond the constraint of working only with straightedge and compass, and the Greeks knew how to solve them in this way. One such example is Archimedes' Neusis construction solution of the problem of Angle trisection.)[27]
In particular, the algebraic formulation of constructible numbers leads to a proof of the impossibility of the following construction problems:
- Doubling the cube
- The problem of doubling the unit square is solved by the construction of another square on the diagonal of the first one, with side length [math]\displaystyle{ \sqrt2 }[/math] and area [math]\displaystyle{ 2 }[/math]. Analogously, the problem of doubling the cube asks for the construction of the length [math]\displaystyle{ \sqrt[3]{2} }[/math] of the side of a cube with volume [math]\displaystyle{ 2 }[/math]. It is not constructible, because the minimal polynomial of this length, [math]\displaystyle{ x^3-2 }[/math], has degree 3 over [math]\displaystyle{ \Q }[/math].[28] As a cubic polynomial whose only real root is irrational, this polynomial must be irreducible, because if it had a quadratic real root then the quadratic conjugate would provide a second real root.[29]
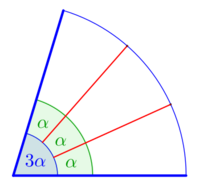
- Angle trisection
- In this problem, from a given angle [math]\displaystyle{ \theta }[/math], one should construct an angle [math]\displaystyle{ \theta/3 }[/math]. Algebraically, angles can be represented by their trigonometric functions, such as their sines or cosines, which give the Cartesian coordinates of the endpoint of a line segment forming the given angle with the initial segment. Thus, an angle [math]\displaystyle{ \theta }[/math] is constructible when [math]\displaystyle{ x=\cos\theta }[/math] is a constructible number, and the problem of trisecting the angle can be formulated as one of constructing [math]\displaystyle{ \cos(\tfrac{1}{3}\arccos x) }[/math]. For example, the angle [math]\displaystyle{ \theta=\pi/3=60^\circ }[/math] of an equilateral triangle can be constructed by compass and straightedge, with [math]\displaystyle{ x=\cos\theta=\tfrac12 }[/math]. However, its trisection [math]\displaystyle{ \theta/3=\pi/9=20^\circ }[/math] cannot be constructed, because [math]\displaystyle{ \cos\pi/9 }[/math] has minimal polynomial [math]\displaystyle{ 8x^3-6x-1 }[/math] of degree 3 over [math]\displaystyle{ \Q }[/math]. Because this specific instance of the trisection problem cannot be solved by compass and straightedge, the general problem also cannot be solved.[30]
- Squaring the circle
- A square with area [math]\displaystyle{ \pi }[/math], the same area as a unit circle, would have side length [math]\displaystyle{ \sqrt\pi }[/math], a transcendental number. Therefore, this square and its side length are not constructible, because it is not algebraic over [math]\displaystyle{ \Q }[/math].[31]
- Regular polygons
- If a regular [math]\displaystyle{ n }[/math]-gon is constructed with its center at the origin, the angles between the segments from the center to consecutive vertices are [math]\displaystyle{ 2\pi/n }[/math]. The polygon can be constructed only when the cosine of this angle is a trigonometric number. Thus, for instance, a 15-gon is constructible, but the regular heptagon is not constructible, because 7 is prime but not a Fermat prime.[32] For a more direct proof of its non-constructibility, represent the vertices of a regular heptagon as the complex roots of the polynomial [math]\displaystyle{ x^7-1 }[/math]. Removing the factor [math]\displaystyle{ x-1 }[/math], dividing by [math]\displaystyle{ x^3 }[/math], and substituting [math]\displaystyle{ y=x+1/x }[/math] gives the simpler polynomial [math]\displaystyle{ y^3+y^2-2y-1 }[/math], an irreducible cubic with three real roots, each two times the real part of a complex-number vertex. Its roots are not constructible, so the heptagon is also not constructible.[33]
- Alhazen's problem
- If two points and a circular mirror are given, where on the circle does one of the given points see the reflected image of the other? Geometrically, the lines from each given point to the point of reflection meet the circle at equal angles and in equal-length chords. However, it is impossible to construct a point of reflection using a compass and straightedge. In particular, for a unit circle with the two points [math]\displaystyle{ (\tfrac16,\tfrac16) }[/math] and [math]\displaystyle{ (-\tfrac12,\tfrac12) }[/math] inside it, the solution has coordinates forming roots of an irreducible degree-four polynomial [math]\displaystyle{ x^4-2x^3+4x^2+2x-1 }[/math]. Although its degree is a power of two, the splitting field of this polynomial has degree divisible by three, so it does not come from an iterated quadratic extension and Alhazen's problem has no compass and straightedge solution.[34]
History
The birth of the concept of constructible numbers is inextricably linked with the history of the three impossible compass and straightedge constructions: doubling the cube, trisecting an angle, and squaring the circle. The restriction of using only compass and straightedge in geometric constructions is often credited to Plato due to a passage in Plutarch. According to Plutarch, Plato gave the duplication of the cube (Delian) problem to Eudoxus and Archytas and Menaechmus, who solved the problem using mechanical means, earning a rebuke from Plato for not solving the problem using pure geometry.[35] However, this attribution is challenged,[36] due, in part, to the existence of another version of the story (attributed to Eratosthenes by Eutocius of Ascalon) that says that all three found solutions but they were too abstract to be of practical value.[37] Proclus, citing Eudemus of Rhodes, credited Oenopides (circa 450 BCE) with two ruler and compass constructions, leading some authors to hypothesize that Oenopides originated the restriction.[38] The restriction to compass and straightedge is essential to the impossibility of the classic construction problems. Angle trisection, for instance, can be done in many ways, several known to the ancient Greeks. The Quadratrix of Hippias of Elis, the conics of Menaechmus, or the marked straightedge (neusis) construction of Archimedes have all been used, as has a more modern approach via paper folding.[39]
Although not one of the classic three construction problems, the problem of constructing regular polygons with straightedge and compass is often treated alongside them. The Greeks knew how to construct regular [math]\displaystyle{ n }[/math]-gons with [math]\displaystyle{ n=2^h }[/math] (for any integer [math]\displaystyle{ h\ge 2 }[/math]), 3, 5, or the product of any two or three of these numbers, but other regular [math]\displaystyle{ n }[/math]-gons eluded them. In 1796 Carl Friedrich Gauss, then an eighteen-year-old student, announced in a newspaper that he had constructed a regular 17-gon with straightedge and compass.[40] Gauss's treatment was algebraic rather than geometric; in fact, he did not actually construct the polygon, but rather showed that the cosine of a central angle was a constructible number. The argument was generalized in his 1801 book Disquisitiones Arithmeticae giving the sufficient condition for the construction of a regular [math]\displaystyle{ n }[/math]-gon. Gauss claimed, but did not prove, that the condition was also necessary and several authors, notably Felix Klein,[41] attributed this part of the proof to him as well.[42] Alhazen's problem is also not one of the classic three problems, but despite being named after Ibn al-Haytham (Alhazen), a medieval Islamic mathematician, it already appear's in Ptolemy's work on optics from the second century.[20]
Pierre Wantzel (1837) proved algebraically that the problems of doubling the cube and trisecting the angle are impossible to solve if one uses only compass and straightedge. In the same paper he also solved the problem of determining which regular polygons are constructible: a regular polygon is constructible if and only if the number of its sides is the product of a power of two and any number of distinct Fermat primes (i.e., the sufficient conditions given by Gauss are also necessary).[24][43] An attempted proof of the impossibility of squaring the circle was given by James Gregory in Vera Circuli et Hyperbolae Quadratura (The True Squaring of the Circle and of the Hyperbola) in 1667. Although his proof was faulty, it was the first paper to attempt to solve the problem using algebraic properties of π. It was not until 1882 that Ferdinand von Lindemann rigorously proved its impossibility, by extending the work of Charles Hermite and proving that π is a transcendental number.[44][45] Alhazen's problem was not proved impossible to solve by compass and straightedge until the work of (Elkin 1965).[46]
The study of constructible numbers, per se, was initiated by René Descartes in La Géométrie, an appendix to his book Discourse on the Method published in 1637. Descartes associated numbers to geometrical line segments in order to display the power of his philosophical method by solving an ancient straightedge and compass construction problem put forth by Pappus.[47]
See also
Notes
- ↑ (Kazarinoff 2003); (Martin 1998), Corollary 2.16, p. 41.
- ↑ Martin (1998), pp. 31–32.
- ↑ Courant & Robbins (1996), Section III.2.2, "All constructible numbers are algebraic", pp. 133–134.
- ↑ Kazarinoff (2003), p. 46.
- ↑ 5.0 5.1 Kazarinoff (2003), p. 10.
- ↑ 6.0 6.1 Martin (1998), Definition 2.1, pp. 30–31.
- ↑ This construction for the midpoint is given in Book I, Proposition 10 of Euclid's Elements.
- ↑ Kazarinoff (2003), p. 18.
- ↑ (Herstein 1986). To use the length-based definition, it is necessary to include the number zero as a constructible number, as a special case.
- ↑ (Moise 1974), p. 227; (Martin 1998), Theorem 2.4, p. 33.
- ↑ Martin (1998), pp. 36–37.
- ↑ Roman (1995), p. 207.
- ↑ 13.0 13.1 (Lawrence Zorzitto), p. 440.
- ↑ For the addition and multiplication formula, see (Kay 2021), Theorem 8.1.10, p. 187. For the division formula, see (Kay 2021), Equations 8.8, p. 188, and 9.2, p. 224. The expansion of the square root can be derived from the half-angle formula of trigonometry; see an equivalent formula at (Lawrence Zorzitto), p. 440.
- ↑ (Herstein 1986); (Moise 1974); (Fraleigh 1994); (Courant Robbins).
- ↑ (Martin 1998); (Courant Robbins).
- ↑ Martin (1998), Theorem 2.7, p. 35.
- ↑ Fraleigh (1994), p. 429.
- ↑ Roman (1995), p. 59.
- ↑ 20.0 20.1 Neumann (1998).
- ↑ Rotman (2006), p. 361.
- ↑ Rotman (2006), p. 362.
- ↑ Martin (1998), Theorem 2.10, p. 37.
- ↑ 24.0 24.1 Martin (1998), p. 46.
- ↑ Stewart (1989), p. 51.
- ↑ Klein (1897), p. 3.
- ↑ The description of these alternative solutions makes up much of the content of (Knorr 1986).
- ↑ (Klein 1897); (Fraleigh 1994)
- ↑ Courant & Robbins (1996), Section III.3.1, "Doubling the cube", pp. 134–135.
- ↑ (Fraleigh 1994); (Courant Robbins)
- ↑ Fraleigh (1994), pp. 429–430.
- ↑ Fraleigh (1994), p. 504.
- ↑ Courant & Robbins (1996), Section III.3.4 "The regular heptagon", pp. 138–139.
- ↑ (Neumann 1998). (Elkin 1965) comes to the same conclusion using different points and a different polynomial.
- ↑ Plutarch, Quaestiones convivales VIII.ii , 718ef.
- ↑ Kazarinoff (2003), p. 28.
- ↑ Knorr (1986), p. 4.
- ↑ Knorr (1986), pp. 15–17.
- ↑ Friedman (2018), pp. 1–3.
- ↑ Kazarinoff (2003), p. 29.
- ↑ Klein (1897), p. 16.
- ↑ Kazarinoff (2003), p. 30.
- ↑ Wantzel (1837).
- ↑ Martin (1998), p. 44.
- ↑ Klein (1897), Chapter IV: The transcendence of the number π, pp. 68–77..
- ↑ (Elkin 1965); see also (Neumann 1998) for an independent solution with more of the history of the problem.
- ↑ Boyer (2004), pp. 83–88.
References
- Boyer, Carl B. (2004), History of Analytic Geometry, Dover, ISBN 978-0-486-43832-0
- Courant, Richard; Robbins, Herbert (1996), "Chapter III: Geometrical constructions, the algebra of number fields", What is Mathematics? An elementary approach to ideas and methods (2nd ed.), Oxford University Press, pp. 117–164, ISBN 0-19-510519-2
- Elkin, Jack M. (March 1965), "A deceptively easy problem", The Mathematics Teacher 58 (3): 194–199, doi:10.5951/MT.58.3.0194
- Fraleigh, John B. (1994), A First Course in Abstract Algebra (5th ed.), Addison Wesley, ISBN 978-0-201-53467-2
- Friedman, Michael (2018), A History of Folding in Mathematics: Mathematizing the Margins, Science Networks. Historical Studies, 59, Birkhäuser, doi:10.1007/978-3-319-72487-4, ISBN 978-3-319-72486-7
- Herstein, I. N. (1986), Abstract Algebra, Macmillan, ISBN 0-02-353820-1
- Kay, Anthony (2021), Number Systems: A Path into Rigorous Mathematics, Taylor & Francis, ISBN 978-0-367-18065-2
- Kazarinoff, Nicholas D. (2003), Ruler and the Round: Classic Problems in Geometric Constructions, Dover, ISBN 0-486-42515-0
- Klein, Felix (1897), Famous Problems of Elementary Geometry, Ginn & Co, https://archive.org/details/famousproblemse00kleigoog
- Knorr, Wilbur Richard (1986), The Ancient Tradition of Geometric Problems, Dover Books on Mathematics, Courier Dover Publications, ISBN 978-0-486-67532-9
- Lawrence, John W.; Zorzitto, Frank A. (2021), Abstract Algebra: A Comprehensive Introduction, Cambridge Mathematical Textbooks, Cambridge University Press, ISBN 978-1-108-86551-7
- Martin, George E. (1998), Geometric Constructions, Undergraduate Texts in Mathematics, Springer-Verlag, New York, doi:10.1007/978-1-4612-0629-3, ISBN 0-387-98276-0
- Moise, Edwin E. (1974), Elementary Geometry from an Advanced Standpoint (2nd ed.), Addison Wesley, ISBN 0-201-04793-4
- Neumann, Peter M. (1998), "Reflections on reflection in a spherical mirror", American Mathematical Monthly 105 (6): 523–528, doi:10.2307/2589403
- Roman, Steven (1995), Field Theory, Springer-Verlag, ISBN 978-0-387-94408-1
- Rotman, Joseph J. (2006), A First Course in Abstract Algebra with Applications (3rd ed.), Prentice Hall, ISBN 978-0-13-186267-8
- Stewart, Ian (1989), Galois Theory (2nd ed.), Chapman and Hall, ISBN 978-0-412-34550-0
- Wantzel, P. L. (1837), "Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas", Journal de Mathématiques Pures et Appliquées 1 (2): 366–372, http://visualiseur.bnf.fr/ConsulterElementNum?O=NUMM-16381&Deb=374&Fin=380&E=PDF
External links
- Weisstein, Eric W.. "Constructible Number". http://mathworld.wolfram.com/ConstructibleNumber.html.
- Constructible Numbers at Cut-the-knot
 |