Feistel cipher
In cryptography, a Feistel cipher (also known as Luby–Rackoff block cipher) is a symmetric structure used in the construction of block ciphers, named after the Germany -born physicist and cryptographer Horst Feistel, who did pioneering research while working for IBM; it is also commonly known as a Feistel network. A large proportion of block ciphers use the scheme, including the US Data Encryption Standard, the Soviet/Russian GOST and the more recent Blowfish and Twofish ciphers. In a Feistel cipher, encryption and decryption are very similar operations, and both consist of iteratively running a function called a "round function" a fixed number of times.
History
Many modern symmetric block ciphers are based on Feistel networks. Feistel networks were first seen commercially in IBM's Lucifer cipher, designed by Horst Feistel and Don Coppersmith in 1973. Feistel networks gained respectability when the U.S. Federal Government adopted the DES (a cipher based on Lucifer, with changes made by the NSA) in 1976. Like other components of the DES, the iterative nature of the Feistel construction makes implementing the cryptosystem in hardware easier (particularly on the hardware available at the time of DES's design).
Design
A Feistel network uses a round function, a function which takes two inputs – a data block and a subkey – and returns one output of the same size as the data block.[1] In each round, the round function is run on half of the data to be encrypted, and its output is XORed with the other half of the data. This is repeated a fixed number of times, and the final output is the encrypted data. An important advantage of Feistel networks compared to other cipher designs such as substitution–permutation networks is that the entire operation is guaranteed to be invertible (that is, encrypted data can be decrypted), even if the round function is not itself invertible. The round function can be made arbitrarily complicated, since it does not need to be designed to be invertible.[2]:465 [3]:347 Furthermore, the encryption and decryption operations are very similar, even identical in some cases, requiring only a reversal of the key schedule. Therefore, the size of the code or circuitry required to implement such a cipher is nearly halved.
Theoretical work
The structure and properties of Feistel ciphers have been extensively analyzed by cryptographers.
Michael Luby and Charles Rackoff analyzed the Feistel cipher construction and proved that if the round function is a cryptographically secure pseudorandom function, with Ki used as the seed, then 3 rounds are sufficient to make the block cipher a pseudorandom permutation, while 4 rounds are sufficient to make it a "strong" pseudorandom permutation (which means that it remains pseudorandom even to an adversary who gets oracle access to its inverse permutation).[4] Because of this very important result of Luby and Rackoff, Feistel ciphers are sometimes called Luby–Rackoff block ciphers.
Further theoretical work has generalized the construction somewhat and given more precise bounds for security.[5][6]
Construction details
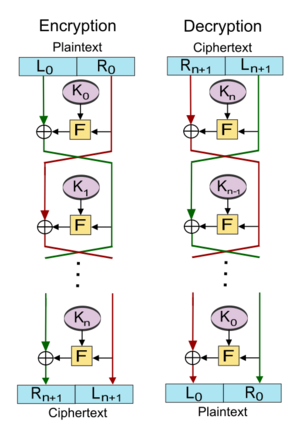
Let [math]\displaystyle{ \mathrm{F} }[/math] be the round function and let [math]\displaystyle{ K_0, K_1, \ldots, K_n }[/math] be the sub-keys for the rounds [math]\displaystyle{ 0, 1, \ldots, n }[/math] respectively.
Then the basic operation is as follows:
Split the plaintext block into two equal pieces: ([math]\displaystyle{ L_0 }[/math], [math]\displaystyle{ R_0 }[/math]).
For each round [math]\displaystyle{ i = 0, 1, \dots, n }[/math], compute
- [math]\displaystyle{ L_{i+1} = R_i, }[/math]
- [math]\displaystyle{ R_{i+1}= L_i \oplus \mathrm{F}(R_i, K_i), }[/math]
where [math]\displaystyle{ \oplus }[/math] means XOR. Then the ciphertext is [math]\displaystyle{ (R_{n+1}, L_{n+1}) }[/math].
Decryption of a ciphertext [math]\displaystyle{ (R_{n+1}, L_{n+1}) }[/math] is accomplished by computing for [math]\displaystyle{ i = n, n - 1, \ldots, 0 }[/math]
- [math]\displaystyle{ R_{i} = L_{i+1}, }[/math]
- [math]\displaystyle{ L_{i} = R_{i+1} \oplus \operatorname{F}(L_{i+1}, K_i). }[/math]
Then [math]\displaystyle{ (L_0, R_0) }[/math] is the plaintext again.
The diagram illustrates both encryption and decryption. Note the reversal of the subkey order for decryption; this is the only difference between encryption and decryption.
Unbalanced Feistel cipher
Unbalanced Feistel ciphers use a modified structure where [math]\displaystyle{ L_0 }[/math] and [math]\displaystyle{ R_0 }[/math] are not of equal lengths.[7] The Skipjack cipher is an example of such a cipher. The Texas Instruments digital signature transponder uses a proprietary unbalanced Feistel cipher to perform challenge–response authentication.[8]
The Thorp shuffle is an extreme case of an unbalanced Feistel cipher in which one side is a single bit. This has better provable security than a balanced Feistel cipher but requires more rounds.[9]
Other uses
The Feistel construction is also used in cryptographic algorithms other than block ciphers. For example, the optimal asymmetric encryption padding (OAEP) scheme uses a simple Feistel network to randomize ciphertexts in certain asymmetric-key encryption schemes.
A generalized Feistel algorithm can be used to create strong permutations on small domains of size not a power of two (see format-preserving encryption).[9]
Feistel networks as a design component
Whether the entire cipher is a Feistel cipher or not, Feistel-like networks can be used as a component of a cipher's design. For example, MISTY1 is a Feistel cipher using a three-round Feistel network in its round function, Skipjack is a modified Feistel cipher using a Feistel network in its G permutation, and Threefish (part of Skein) is a non-Feistel block cipher that uses a Feistel-like MIX function.
List of Feistel ciphers
Feistel or modified Feistel:
|
|
|
Generalised Feistel:
- CAST-256
- CLEFIA
- MacGuffin
- RC2
- RC6
- Skipjack
- SMS4
See also
- Cryptography
- Stream cipher
- Substitution–permutation network
- Lifting scheme for discrete wavelet transform has pretty much the same structure
- Format-preserving encryption
- Lai–Massey scheme
References
- ↑ Menezes, Alfred J.; Oorschot, Paul C. van; Vanstone, Scott A. (2001). Handbook of Applied Cryptography (Fifth ed.). Taylor & Francis. p. 251. ISBN 978-0849385230. https://archive.org/details/handbookofapplie0000mene/page/251.
- ↑ Schneier, Bruce (1996). Applied Cryptography. New York: John Wiley & Sons. ISBN 0-471-12845-7.
- ↑ Stinson, Douglas R. (1995). Cryptography: Theory and Practice. Boca Raton: CRC Press. ISBN 0-8493-8521-0.
- ↑ Luby, Michael; Rackoff, Charles (April 1988), "How to Construct Pseudorandom Permutations from Pseudorandom Functions", SIAM Journal on Computing 17 (2): 373–386, doi:10.1137/0217022, ISSN 0097-5397.
- ↑ Patarin, Jacques (October 2003), Boneh, Dan, ed., Advances in Cryptology - CRYPTO 2003, Lecture Notes in Computer Science, 2729, pp. 513–529, doi:10.1007/b11817, ISBN 978-3-540-40674-7, https://www.iacr.org/archive/crypto2003/27290510/27290510.pdf, retrieved 2009-07-27
- ↑ Zheng, Yuliang; Matsumoto, Tsutomu; Imai, Hideki (1989-08-20). "On the Construction of Block Ciphers Provably Secure and Not Relying on Any Unproved Hypotheses" (in en). Advances in Cryptology — CRYPTO' 89 Proceedings. Lecture Notes in Computer Science. 435. pp. 461–480. doi:10.1007/0-387-34805-0_42. ISBN 978-0-387-97317-3.
- ↑ Schneier, Bruce; Kelsey, John (1996-02-21). "Unbalanced Feistel networks and block cipher design" (in en). Fast Software Encryption. Lecture Notes in Computer Science. 1039. pp. 121–144. doi:10.1007/3-540-60865-6_49. ISBN 978-3-540-60865-3. https://www.schneier.com/academic/paperfiles/paper-unbalanced-feistel.ps.gz. Retrieved 2017-11-21.
- ↑ Bono, Stephen; Green, Matthew; Stubblefield, Adam; Juels, Ari; Rubin, Aviel; Szydlo, Michael (2005-08-05). "Security Analysis of a Cryptographically-Enabled RFID Device". Proceedings of the USENIX Security Symposium. https://www.usenix.org/event/sec05/tech/bono/bono.pdf. Retrieved 2017-11-21.
- ↑ 9.0 9.1 Morris, Ben; Rogaway, Phillip; Stegers, Till (2009). "How to Encipher Messages on a Small Domain" (in en). Advances in Cryptology - CRYPTO 2009. Lecture Notes in Computer Science. 5677. pp. 286–302. doi:10.1007/978-3-642-03356-8_17. ISBN 978-3-642-03355-1. http://www.cs.ucdavis.edu/~rogaway/papers/thorp.pdf. Retrieved 2017-11-21.
 |