Block cipher mode of operation
In cryptography, a block cipher mode of operation is an algorithm that uses a block cipher to provide information security such as confidentiality or authenticity.[1] A block cipher by itself is only suitable for the secure cryptographic transformation (encryption or decryption) of one fixed-length group of bits called a block.[2] A mode of operation describes how to repeatedly apply a cipher's single-block operation to securely transform amounts of data larger than a block.[3][4][5]
Most modes require a unique binary sequence, often called an initialization vector (IV), for each encryption operation. The IV has to be non-repeating and, for some modes, random as well. The initialization vector is used to ensure distinct ciphertexts are produced even when the same plaintext is encrypted multiple times independently with the same key.[6] Block ciphers may be capable of operating on more than one block size, but during transformation the block size is always fixed. Block cipher modes operate on whole blocks and require that the last part of the data be padded to a full block if it is smaller than the current block size.[2] There are, however, modes that do not require padding because they effectively use a block cipher as a stream cipher.
Historically, encryption modes have been studied extensively in regard to their error propagation properties under various scenarios of data modification. Later development regarded integrity protection as an entirely separate cryptographic goal. Some modern modes of operation combine confidentiality and authenticity in an efficient way, and are known as authenticated encryption modes.[7]
History and standardization
The earliest modes of operation, ECB, CBC, OFB, and CFB (see below for all), date back to 1981 and were specified in FIPS 81, DES Modes of Operation. In 2001, the US National Institute of Standards and Technology (NIST) revised its list of approved modes of operation by including AES as a block cipher and adding CTR mode in SP800-38A, Recommendation for Block Cipher Modes of Operation. Finally, in January, 2010, NIST added XTS-AES in SP800-38E, Recommendation for Block Cipher Modes of Operation: The XTS-AES Mode for Confidentiality on Storage Devices. Other confidentiality modes exist which have not been approved by NIST. For example, CTS is ciphertext stealing mode and available in many popular cryptographic libraries.
The block cipher modes ECB, CBC, OFB, CFB, CTR, and XTS provide confidentiality, but they do not protect against accidental modification or malicious tampering. Modification or tampering can be detected with a separate message authentication code such as CBC-MAC, or a digital signature. The cryptographic community recognized the need for dedicated integrity assurances and NIST responded with HMAC, CMAC, and GMAC. HMAC was approved in 2002 as FIPS 198, The Keyed-Hash Message Authentication Code (HMAC), CMAC was released in 2005 under SP800-38B, Recommendation for Block Cipher Modes of Operation: The CMAC Mode for Authentication, and GMAC was formalized in 2007 under SP800-38D, Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC.
The cryptographic community observed that compositing (combining) a confidentiality mode with an authenticity mode could be difficult and error prone. They therefore began to supply modes which combined confidentiality and data integrity into a single cryptographic primitive (an encryption algorithm). These combined modes are referred to as authenticated encryption, AE or "authenc". Examples of AE modes are CCM (SP800-38C), GCM (SP800-38D), CWC, EAX, IAPM, and OCB.
Modes of operation are defined by a number of national and internationally recognized standards bodies. Notable standards organizations include NIST, ISO (with ISO/IEC 10116[5]), the IEC, the IEEE, ANSI, and the IETF.
Initialization vector (IV)
An initialization vector (IV) or starting variable (SV)[5] is a block of bits that is used by several modes to randomize the encryption and hence to produce distinct ciphertexts even if the same plaintext is encrypted multiple times, without the need for a slower re-keying process.[citation needed]
An initialization vector has different security requirements than a key, so the IV usually does not need to be secret. For most block cipher modes it is important that an initialization vector is never reused under the same key, i.e. it must be a cryptographic nonce. Many block cipher modes have stronger requirements, such as the IV must be random or pseudorandom. Some block ciphers have particular problems with certain initialization vectors, such as all zero IV generating no encryption (for some keys).
It is recommended to review relevant IV requirements for the particular block cipher mode in relevant specification, for example SP800-38A.
For CBC and CFB, reusing an IV leaks some information about the first block of plaintext, and about any common prefix shared by the two messages.
For OFB and CTR, reusing an IV causes key bitstream re-use, which breaks security.[8] This can be seen because both modes effectively create a bitstream that is XORed with the plaintext, and this bitstream is dependent on the key and IV only.
In CBC mode, the IV must be unpredictable (random or pseudorandom) at encryption time; in particular, the (previously) common practice of re-using the last ciphertext block of a message as the IV for the next message is insecure (for example, this method was used by SSL 2.0). If an attacker knows the IV (or the previous block of ciphertext) before the next plaintext is specified, they can check their guess about plaintext of some block that was encrypted with the same key before (this is known as the TLS CBC IV attack).[9]
For some keys, an all-zero initialization vector may generate some block cipher modes (CFB-8, OFB-8) to get the internal state stuck at all-zero. For CFB-8, an all-zero IV and an all-zero plaintext, causes 1/256 of keys to generate no encryption, plaintext is returned as ciphertext.[10] For OFB-8, using all zero initialization vector will generate no encryption for 1/256 of keys.[11] OFB-8 encryption returns the plaintext unencrypted for affected keys.
Some modes (such as AES-SIV and AES-GCM-SIV) are built to be more nonce-misuse resistant, i.e. resilient to scenarios in which the randomness generation is faulty or under the control of the attacker.
- Synthetic initialization vectors (SIV) synthesize an internal IV by running a pseudo-random function (PRF) construction called S2V on the input (additional data and plaintext), preventing any external data from directly controlling the IV. External nonces / IV may be fed into S2V as an additional data field.
- AES-GCM-SIVs synthesize an internal IV by running POLYVAL Galois mode of authentication on input (additional data and plaintext), followed by an AES operation.
Padding
A block cipher works on units of a fixed size (known as a block size), but messages come in a variety of lengths. So some modes (namely ECB and CBC) require that the final block be padded before encryption. Several padding schemes exist. The simplest is to add null bytes to the plaintext to bring its length up to a multiple of the block size, but care must be taken that the original length of the plaintext can be recovered; this is trivial, for example, if the plaintext is a C style string which contains no null bytes except at the end. Slightly more complex is the original DES method, which is to add a single one bit, followed by enough zero bits to fill out the block; if the message ends on a block boundary, a whole padding block will be added. Most sophisticated are CBC-specific schemes such as ciphertext stealing or residual block termination, which do not cause any extra ciphertext, at the expense of some additional complexity. Schneier and Ferguson suggest two possibilities, both simple: append a byte with value 128 (hex 80), followed by as many zero bytes as needed to fill the last block, or pad the last block with n bytes all with value n.
CFB, OFB and CTR modes do not require any special measures to handle messages whose lengths are not multiples of the block size, since the modes work by XORing the plaintext with the output of the block cipher. The last partial block of plaintext is XORed with the first few bytes of the last keystream block, producing a final ciphertext block that is the same size as the final partial plaintext block. This characteristic of stream ciphers makes them suitable for applications that require the encrypted ciphertext data to be the same size as the original plaintext data, and for applications that transmit data in streaming form where it is inconvenient to add padding bytes.
Common modes
Authenticated encryption with additional data (AEAD) modes
A number of modes of operation have been designed to combine secrecy and authentication in a single cryptographic primitive. Examples of such modes are ,[12] integrity-aware cipher block chaining (IACBC)[clarification needed], integrity-aware parallelizable mode (IAPM),[13] OCB, EAX, CWC, CCM, and GCM. Authenticated encryption modes are classified as single-pass modes or double-pass modes. Some single-pass authenticated encryption algorithms, such as OCB mode, are encumbered by patents, while others were specifically designed and released in a way to avoid such encumberment.
In addition, some modes also allow for the authentication of unencrypted associated data, and these are called AEAD (authenticated encryption with associated data) schemes. For example, EAX mode is a double-pass AEAD scheme while OCB mode is single-pass.
Galois/counter (GCM)
| GCM | |
|---|---|
| Galois/counter | |
| Encryption parallelizable | Yes |
| Decryption parallelizable | Yes |
| Random read access | Yes |
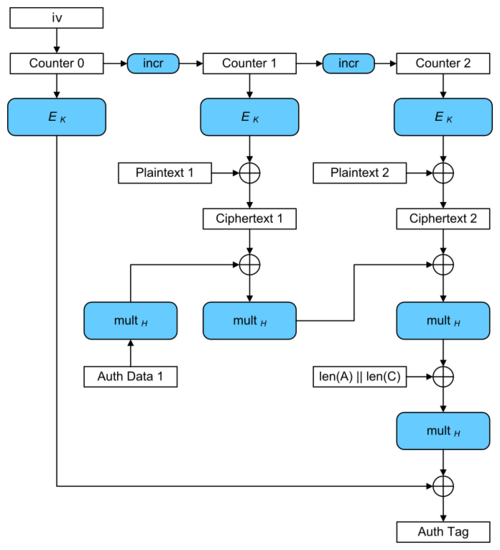
Galois/counter mode (GCM) combines the well-known counter mode of encryption with the new Galois mode of authentication. The key feature is the ease of parallel computation of the Galois field multiplication used for authentication. This feature permits higher throughput than encryption algorithms.
GCM is defined for block ciphers with a block size of 128 bits. Galois message authentication code (GMAC) is an authentication-only variant of the GCM which can form an incremental message authentication code. Both GCM and GMAC can accept initialization vectors of arbitrary length. GCM can take full advantage of parallel processing and implementing GCM can make efficient use of an instruction pipeline or a hardware pipeline. The CBC mode of operation incurs pipeline stalls that hamper its efficiency and performance.
Like in CTR, blocks are numbered sequentially, and then this block number is combined with an IV and encrypted with a block cipher E, usually AES. The result of this encryption is then XORed with the plaintext to produce the ciphertext. Like all counter modes, this is essentially a stream cipher, and so it is essential that a different IV is used for each stream that is encrypted.
The ciphertext blocks are considered coefficients of a polynomial which is then evaluated at a key-dependent point H, using finite field arithmetic. The result is then encrypted, producing an authentication tag that can be used to verify the integrity of the data. The encrypted text then contains the IV, ciphertext, and authentication tag.
Counter with cipher block chaining message authentication code (CCM)
Counter with cipher block chaining message authentication code (counter with CBC-MAC; CCM) is an authenticated encryption algorithm designed to provide both authentication and confidentiality. CCM mode is only defined for block ciphers with a block length of 128 bits.[14][15]
Synthetic initialization vector (SIV)
Synthetic initialization vector (SIV) is a nonce-misuse resistant block cipher mode.
SIV synthesizes an internal IV using the pseudorandom function S2V. S2V is a keyed hash is based on CMAC, and the input to the function is:
- Additional authenticated data (zero, one or many AAD fields are supported)
- Plaintext
- Authentication key (K1).
SIV encrypts the S2V output and the plaintext using AES-CTR, keyed with the encryption key (K2).
SIV can support external nonce-based authenticated encryption, in which case one of the authenticated data fields is utilized for this purpose. RFC5297[16] specifies that for interoperability purposes the last authenticated data field should be used external nonce.
Owing to the use of two keys, the authentication key K1 and encryption key K2, naming schemes for SIV AEAD-variants may lead to some confusion; for example AEAD_AES_SIV_CMAC_256 refers to AES-SIV with two AES-128 keys and not AES-256.
AES-GCM-SIV
AES-GCM-SIV is a mode of operation for the Advanced Encryption Standard which provides similar performance to Galois/counter mode as well as misuse resistance in the event of the reuse of a cryptographic nonce. The construction is defined in RFC 8452.[17]
AES-GCM-SIV synthesizes the internal IV. It derives a hash of the additional authenticated data and plaintext using the POLYVAL Galois hash function. The hash is then encrypted an AES-key, and used as authentication tag and AES-CTR initialization vector.
AES-GCM-SIV is an improvement over the very similarly named algorithm GCM-SIV, with a few very small changes (e.g. how AES-CTR is initialized), but which yields practical benefits to its security "This addition allows for encrypting up to 250 messages with the same key, compared to the significant limitation of only 232 messages that were allowed with GCM-SIV."[18]
Confidentiality only modes
Many modes of operation have been defined. Some of these are described below. The purpose of cipher modes is to mask patterns which exist in encrypted data, as illustrated in the description of the weakness of ECB.
Different cipher modes mask patterns by cascading outputs from the cipher block or other globally deterministic variables into the subsequent cipher block. The inputs of the listed modes are summarized in the following table:
| Mode | Formulas | Ciphertext | |
|---|---|---|---|
| Electronic codebook | (ECB) | Yi = F(PlainTexti, Key) | Yi |
| Cipher block chaining | (CBC) | Yi = PlainTexti XOR Ciphertexti−1 | F(Y, Key); Ciphertext0 = IV |
| Propagating CBC | (PCBC) | Yi = PlainTexti XOR (Ciphertexti−1 XOR PlainTexti−1) | F(Y, Key); Ciphertext0 = IV |
| Cipher feedback | (CFB) | Yi = Ciphertexti−1 | Plaintext XOR F(Y, Key); Ciphertext0 = IV |
| Output feedback | (OFB) | Yi = F(Yi−1, Key); Y0 = F(IV, Key) | Plaintext XOR Yi |
| Counter | (CTR) | Yi = F(IV + g(i), Key); IV = token() | Plaintext XOR Yi |
Note: g(i) is any deterministic function, often the identity function.
Electronic codebook (ECB)
| ECB | |
|---|---|
| Electronic codebook | |
| Encryption parallelizable | Yes |
| Decryption parallelizable | Yes |
| Random read access | Yes |
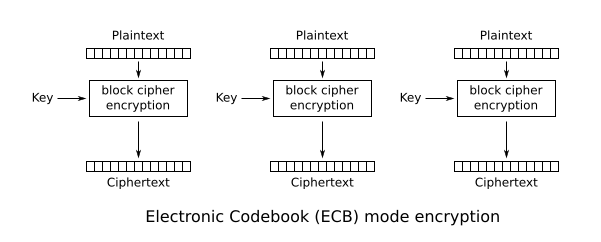
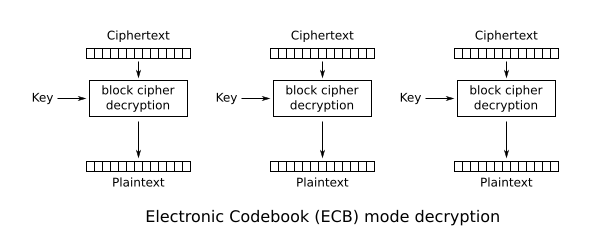
The simplest (and not to be used anymore) of the encryption modes is the electronic codebook (ECB) mode (named after conventional physical codebooks[19]). The message is divided into blocks, and each block is encrypted separately.
The disadvantage of this method is a lack of diffusion. Because ECB encrypts identical plaintext blocks into identical ciphertext blocks, it does not hide data patterns well. ECB is not recommended for use in cryptographic protocols.[20][21][22]
A striking example of the degree to which ECB can leave plaintext data patterns in the ciphertext can be seen when ECB mode is used to encrypt a bitmap image which uses large areas of uniform color. While the color of each individual pixel is encrypted, the overall image may still be discerned, as the pattern of identically colored pixels in the original remains in the encrypted version.
ECB mode can also make protocols without integrity protection even more susceptible to replay attacks, since each block gets decrypted in exactly the same way.[citation needed]
Cipher block chaining (CBC)
| CBC | |
|---|---|
| Cipher block chaining | |
| Encryption parallelizable | No |
| Decryption parallelizable | Yes |
| Random read access | Yes |
Ehrsam, Meyer, Smith and Tuchman invented the cipher block chaining (CBC) mode of operation in 1976.[23] In CBC mode, each block of plaintext is XORed with the previous ciphertext block before being encrypted. This way, each ciphertext block depends on all plaintext blocks processed up to that point. To make each message unique, an initialization vector must be used in the first block.
If the first block has index 1, the mathematical formula for CBC encryption is
- [math]\displaystyle{ C_i = E_K(P_i \oplus C_{i-1}), }[/math]
- [math]\displaystyle{ C_0 = IV, }[/math]
while the mathematical formula for CBC decryption is
- [math]\displaystyle{ P_i = D_K(C_i) \oplus C_{i-1}, }[/math]
- [math]\displaystyle{ C_0 = IV. }[/math]
Example
CBC has been the most commonly used mode of operation. Its main drawbacks are that encryption is sequential (i.e., it cannot be parallelized), and that the message must be padded to a multiple of the cipher block size. One way to handle this last issue is through the method known as ciphertext stealing. Note that a one-bit change in a plaintext or initialization vector (IV) affects all following ciphertext blocks.
Decrypting with the incorrect IV causes the first block of plaintext to be corrupt but subsequent plaintext blocks will be correct. This is because each block is XORed with the ciphertext of the previous block, not the plaintext, so one does not need to decrypt the previous block before using it as the IV for the decryption of the current one. This means that a plaintext block can be recovered from two adjacent blocks of ciphertext. As a consequence, decryption can be parallelized. Note that a one-bit change to the ciphertext causes complete corruption of the corresponding block of plaintext, and inverts the corresponding bit in the following block of plaintext, but the rest of the blocks remain intact. This peculiarity is exploited in different padding oracle attacks, such as POODLE.
Explicit initialization vectors[24] take advantage of this property by prepending a single random block to the plaintext. Encryption is done as normal, except the IV does not need to be communicated to the decryption routine. Whatever IV decryption uses, only the random block is "corrupted". It can be safely discarded and the rest of the decryption is the original plaintext.
Propagating cipher block chaining (PCBC)
| PCBC | |
|---|---|
| Propagating cipher block chaining | |
| Encryption parallelizable | No |
| Decryption parallelizable | No |
| Random read access | No |
The propagating cipher block chaining[25] or plaintext cipher-block chaining[26] mode was designed to cause small changes in the ciphertext to propagate indefinitely when decrypting, as well as when encrypting. In PCBC mode, each block of plaintext is XORed with both the previous plaintext block and the previous ciphertext block before being encrypted. Like with CBC mode, an initialization vector is used in the first block. Unlike CBC, decrypting PCBC with the incorrect IV (initialization vector) causes all blocks of plaintext to be corrupt.
Encryption and decryption algorithms are as follows:
- [math]\displaystyle{ C_i = E_K(P_i \oplus P_{i-1} \oplus C_{i-1}), P_0 \oplus C_0 = IV, }[/math]
- [math]\displaystyle{ P_i = D_K(C_i) \oplus P_{i-1} \oplus C_{i-1}, P_0 \oplus C_0 = IV. }[/math]
PCBC is used in Kerberos v4 and WASTE, most notably, but otherwise is not common. On a message encrypted in PCBC mode, if two adjacent ciphertext blocks are exchanged, this does not affect the decryption of subsequent blocks.[27] For this reason, PCBC is not used in Kerberos v5.
This can be proven very easily. If we have the following ciphertexts, in this exact order: c1, c2, c3. Than the plaintext associated with c3 (noted as p3) has the following value:
p3 = DecAlg(c1) xor iv xor c1 xor DecAlg(c2) xor c2 xor DecAlg(c3).
If we exchange two adjacent ciphertext blocks: c1 and c2, we will have the following ciphertexts, in this exact order: c2, c1, c3. Than the plaintext associated with c3 (noted as p3) has the following value:
p3 = DecAlg(c2) xor iv xor c2 xor DecAlg(c1) xor c1 xor DecAlg(c3).
We can very easily see that the two values of p3 are IDENTICAL because xor is a commutative operation/operator.
Proof done.
Cipher feedback (CFB)
Full-block CFB
| CFB | |
|---|---|
| Cipher feedback | |
| Encryption parallelizable | No |
| Decryption parallelizable | Yes |
| Random read access | Yes |
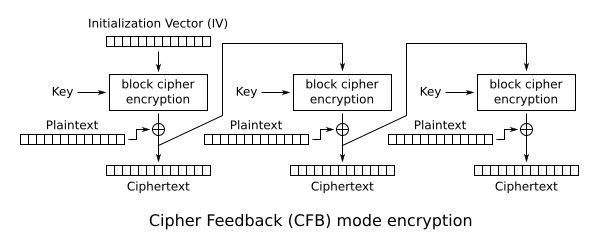
The cipher feedback (CFB) mode, in its simplest form uses the entire output of the block cipher. In this variation, it is very similar to CBC, turning a block cipher into a self-synchronizing stream cipher. CFB decryption in this variation is almost identical to CBC encryption performed in reverse:
- [math]\displaystyle{ \begin{align} C_i &= \begin{cases} \text{IV}, & i = 0 \\ E_K (C_{i-1}) \oplus P_i, & \text{otherwise} \end{cases} \\ P_i &= E_K (C_{i-1}) \oplus C_i, \end{align} }[/math]
CFB-1, CFB-8, CFB-64, CFB-128, etc.
NIST SP800-38A defines CFB with a bit-width.[28] The CFB mode also requires an integer parameter, denoted s, such that 1 ≤ s ≤ b. In the specification of the CFB mode below, each plaintext segment (Pj) and ciphertext segment (Cj) consists of s bits. The value of s is sometimes incorporated into the name of the mode, e.g., the 1-bit CFB mode, the 8-bit CFB mode, the 64-bit CFB mode, or the 128-bit CFB mode.
These modes will truncate the output of the underlying block cipher.
- [math]\displaystyle{ I_0 = \text{IV}. }[/math]
- [math]\displaystyle{ I_i = \big((I_{i-1} \ll s) + C_i\big) \bmod 2^b, }[/math]
- [math]\displaystyle{ C_i = \operatorname{MSB}_s\big(E_K(I_{i-1})\big) \oplus P_i, }[/math]
- [math]\displaystyle{ P_i = \operatorname{MSB}_s\big(E_K(I_{i-1})\big) \oplus C_i, }[/math]
CFB-1 is considered self synchronizing and resilient to loss of ciphertext; "When the 1-bit CFB mode is used, then the synchronization is automatically restored b+1 positions after the inserted or deleted bit. For other values of s in the CFB mode, and for the other confidentiality modes in this recommendation, the synchronization must be restored externally." (NIST SP800-38A). I.e. 1-bit loss in a 128-bit-wide block cipher like AES will render 129 invalid bits before emitting valid bits.
CFB may also self synchronize in some special cases other than those specified. For example, a one bit change in CFB-128 with an underlying 128 bit block cipher, will re-synchronize after two blocks. (However, CFB-128 etc. will not handle bit loss gracefully; a one-bit loss will cause the decryptor to lose alignment with the encryptor)
CFB compared to other modes
Like CBC mode, changes in the plaintext propagate forever in the ciphertext, and encryption cannot be parallelized. Also like CBC, decryption can be parallelized.
CFB, OFB and CTR share two advantages over CBC mode: the block cipher is only ever used in the encrypting direction, and the message does not need to be padded to a multiple of the cipher block size (though ciphertext stealing can also be used for CBC mode to make padding unnecessary).
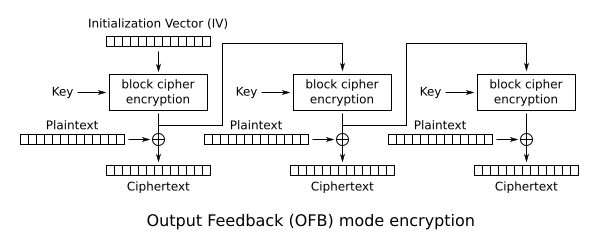
Output feedback (OFB)
| OFB | |
|---|---|
| Output feedback | |
| Encryption parallelizable | No |
| Decryption parallelizable | No |
| Random read access | No |
The output feedback (OFB) mode makes a block cipher into a synchronous stream cipher. It generates keystream blocks, which are then XORed with the plaintext blocks to get the ciphertext. Just as with other stream ciphers, flipping a bit in the ciphertext produces a flipped bit in the plaintext at the same location. This property allows many error-correcting codes to function normally even when applied before encryption.
Because of the symmetry of the XOR operation, encryption and decryption are exactly the same:
- [math]\displaystyle{ C_j = P_j \oplus M_j, }[/math]
- [math]\displaystyle{ P_j = C_j \oplus O_j, }[/math]
- [math]\displaystyle{ O_j = E_K(I_j), }[/math]
- [math]\displaystyle{ I_j = O_{j-1}, }[/math]
- [math]\displaystyle{ I_0 = \text{IV}. }[/math]
Each output feedback block cipher operation depends on all previous ones, and so cannot be performed in parallel. However, because the plaintext or ciphertext is only used for the final XOR, the block cipher operations may be performed in advance, allowing the final step to be performed in parallel once the plaintext or ciphertext is available.
It is possible to obtain an OFB mode keystream by using CBC mode with a constant string of zeroes as input. This can be useful, because it allows the usage of fast hardware implementations of CBC mode for OFB mode encryption.
Using OFB mode with a partial block as feedback like CFB mode reduces the average cycle length by a factor of 232 or more. A mathematical model proposed by Davies and Parkin and substantiated by experimental results showed that only with full feedback an average cycle length near to the obtainable maximum can be achieved. For this reason, support for truncated feedback was removed from the specification of OFB.[29]
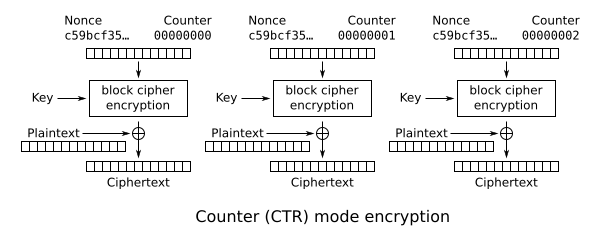
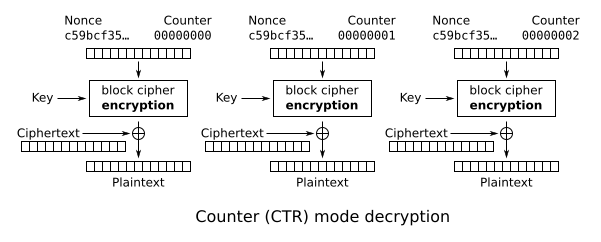
Counter (CTR)
| CTR | |
|---|---|
| Counter | |
| Encryption parallelizable | Yes |
| Decryption parallelizable | Yes |
| Random read access | Yes |
- Note: CTR mode (CM) is also known as integer counter mode (ICM) and segmented integer counter (SIC) mode.
Like OFB, counter mode turns a block cipher into a stream cipher. It generates the next keystream block by encrypting successive values of a "counter". The counter can be any function which produces a sequence which is guaranteed not to repeat for a long time, although an actual increment-by-one counter is the simplest and most popular. The usage of a simple deterministic input function used to be controversial; critics argued that "deliberately exposing a cryptosystem to a known systematic input represents an unnecessary risk".[30] However, today CTR mode is widely accepted, and any problems are considered a weakness of the underlying block cipher, which is expected to be secure regardless of systemic bias in its input.[31] Along with CBC, CTR mode is one of two block cipher modes recommended by Niels Ferguson and Bruce Schneier.[32]
CTR mode was introduced by Whitfield Diffie and Martin Hellman in 1979.[31]
CTR mode has similar characteristics to OFB, but also allows a random-access property during decryption. CTR mode is well suited to operate on a multi-processor machine, where blocks can be encrypted in parallel. Furthermore, it does not suffer from the short-cycle problem that can affect OFB.[33]
If the IV/nonce is random, then they can be combined with the counter using any invertible operation (concatenation, addition, or XOR) to produce the actual unique counter block for encryption. In case of a non-random nonce (such as a packet counter), the nonce and counter should be concatenated (e.g., storing the nonce in the upper 64 bits and the counter in the lower 64 bits of a 128-bit counter block). Simply adding or XORing the nonce and counter into a single value would break the security under a chosen-plaintext attack in many cases, since the attacker may be able to manipulate the entire IV–counter pair to cause a collision. Once an attacker controls the IV–counter pair and plaintext, XOR of the ciphertext with the known plaintext would yield a value that, when XORed with the ciphertext of the other block sharing the same IV–counter pair, would decrypt that block.[34]
Note that the nonce in this diagram is equivalent to the initialization vector (IV) in the other diagrams. However, if the offset/location information is corrupt, it will be impossible to partially recover such data due to the dependence on byte offset.
Error propagation
"Error propagation" properties describe how a decryption behaves during bit errors, i.e. how error in one bit cascades to different decrypted bits.
Bit errors may occur intentionally in attacks or randomly due to transmission errors.
- Random bit errors occur independently in any bit position with an expected probability of ½.
- Specific bit errors occur in the same bit position(s) as the original bit error(s).
- Specific bit errors in stream cipher modes (OFB, CTR, etc.) are trivial. They affect only the specific bit intended.
- Specific bit errors in more complex modes such (e.g. CBC): adaptive chosen-ciphertext attack may intelligently combine many different specific bit errors to break the cipher mode. In Padding oracle attack, CBC can be decrypted in the attack by guessing encryption secrets based on error responses. The Padding Oracle attack variant "CBC-R" (CBC Reverse) lets the attacker construct any valid message.
For modern authenticated encryption (AEAD) or protocols with message authentication codes chained in MAC-Then-Encrypt order, any bit error should completely abort decryption and must not generate any specific bit errors to decryptor. I.e. if decryption succeeded, there should not be any bit error. As such error propagation is less important subject in modern cipher modes than in traditional confidentiality-only modes.
| Mode | Effect of bit errors in Ci | Effect of bit errors in the IV or nonce |
|---|---|---|
| ECB | Random bit errors in Pi | N/A |
| CBC | Random bit errors in Pi Specific bit errors in Pi+1 |
Specific bit errors in P1 |
| CFB | Specific bit errors in Pi Random bit errors in Pi+1, …, until synchronization is restored |
Random bit errors in P1, …, until synchronization is restored |
| OFB | Specific bit errors in Pi | Random bit errors in P1, P2, …, Pn |
| CTR | Specific bit errors in Pi | Random bit errors in Pi for bit error in counter block Ti |
(Source: SP800-38A Table D.2: Summary of Effect of Bit Errors on Decryption)
It might be observed, for example, that a one-block error in the transmitted ciphertext would result in a one-block error in the reconstructed plaintext for ECB mode encryption, while in CBC mode such an error would affect two blocks. Some felt that such resilience was desirable in the face of random errors (e.g., line noise), while others argued that error correcting increased the scope for attackers to maliciously tamper with a message.
However, when proper integrity protection is used, such an error will result (with high probability) in the entire message being rejected. If resistance to random error is desirable, error-correcting codes should be applied to the ciphertext before transmission.
Other modes and other cryptographic primitives
Many more modes of operation for block ciphers have been suggested. Some have been accepted, fully described (even standardized), and are in use. Others have been found insecure, and should never be used. Still others don't categorize as confidentiality, authenticity, or authenticated encryption – for example key feedback mode and Davies–Meyer hashing.
NIST maintains a list of proposed modes for block ciphers at Modes Development.[28][35]
Disk encryption often uses special purpose modes specifically designed for the application. Tweakable narrow-block encryption modes (LRW, XEX, and XTS) and wide-block encryption modes (CMC and EME) are designed to securely encrypt sectors of a disk (see disk encryption theory).
Many modes use an initialization vector (IV) which, depending on the mode, may have requirements such as being only used once (a nonce) or being unpredictable ahead of its publication, etc. Reusing an IV with the same key in CTR, GCM or OFB mode results in XORing the same keystream with two or more plaintexts, a clear misuse of a stream, with a catastrophic loss of security. Deterministic authenticated encryption modes such as the NIST Key Wrap algorithm and the SIV (RFC 5297) AEAD mode do not require an IV as an input, and return the same ciphertext and authentication tag every time for a given plaintext and key. Other IV misuse-resistant modes such as AES-GCM-SIV benefit from an IV input, for example in the maximum amount of data that can be safely encrypted with one key, while not failing catastrophically if the same IV is used multiple times.
Block ciphers can also be used in other cryptographic protocols. They are generally used in modes of operation similar to the block modes described here. As with all protocols, to be cryptographically secure, care must be taken to design these modes of operation correctly.
There are several schemes which use a block cipher to build a cryptographic hash function. See one-way compression function for descriptions of several such methods.
Cryptographically secure pseudorandom number generators (CSPRNGs) can also be built using block ciphers.
Message authentication codes (MACs) are often built from block ciphers. CBC-MAC, OMAC and PMAC are examples.
See also
References
- ↑ NIST Computer Security Division's (CSD) Security Technology Group (STG) (2013). "Block cipher modes". Cryptographic Toolkit. NIST. http://csrc.nist.gov/groups/ST/toolkit/BCM/index.html.
- ↑ 2.0 2.1 Ferguson, N.; Schneier, B.; Kohno, T. (2010). Cryptography Engineering: Design Principles and Practical Applications. Indianapolis: Wiley Publishing, Inc.. pp. 63, 64. ISBN 978-0-470-47424-2.
- ↑ NIST Computer Security Division's (CSD) Security Technology Group (STG) (2013). "Proposed modes". Cryptographic Toolkit. NIST. http://csrc.nist.gov/groups/ST/toolkit/BCM/modes_development.html.
- ↑ Alfred J. Menezes; Paul C. van Oorschot; Scott A. Vanstone (1996). Handbook of Applied Cryptography. CRC Press. pp. 228–233. ISBN 0-8493-8523-7. https://archive.org/details/handbookofapplie0000mene/page/228.
- ↑ 5.0 5.1 5.2 "ISO/IEC 10116:2006 – Information technology – Security techniques – Modes of operation for an n-bit block cipher". ISO Standards Catalogue. 2006. http://www.iso.org/iso/iso_catalogue/catalogue_tc/catalogue_detail.htm?csnumber=38761.
- ↑ Conrad, Eric; Misenar, Seth; Feldman, Joshua (2017-01-01), Conrad, Eric; Misenar, Seth; Feldman, Joshua, eds., "Chapter 3 - Domain 3: Security engineering" (in en), Eleventh Hour CISSP® (Third Edition) (Syngress): pp. 47–93, doi:10.1016/b978-0-12-811248-9.00003-6, ISBN 978-0-12-811248-9, http://www.sciencedirect.com/science/article/pii/B9780128112489000036, retrieved 2020-11-01
- ↑ NIST Computer Security Division's (CSD) Security Technology Group (STG) (2013). "Current modes". Cryptographic Toolkit. NIST. http://csrc.nist.gov/groups/ST/toolkit/BCM/current_modes.html.
- ↑ "Stream Cipher Reuse: A Graphic Example". Cryptosmith LLC. 31 May 2008. http://cryptosmith.com/2008/05/31/stream-reuse/.
- ↑ B. Moeller (May 20, 2004), Security of CBC Ciphersuites in SSL/TLS: Problems and Countermeasures, http://www.openssl.org/~bodo/tls-cbc.txt
- ↑ Tervoort, Tom. "Zerologon: Unauthenticated domain controller compromise by subverting Netlogon cryptography (CVE-2020-1472)". https://www.secura.com/pathtoimg.php?id=2055.
- ↑ Blaufish (14 October 2020). "Netlogon CFB8 considered harmful. OFB8 also.". https://github.com/blaufish/cfb8-vulnerable.
- ↑ Gligor, Virgil D.; Donescu, Pompiliu (2002). "Fast Encryption and Authentication: XCBC Encryption and XECB Authentication Modes". in Matsui, M.. Fast Software Encryption 2001. 2355. Berlin: Springer. pp. 92–108. doi:10.1007/3-540-45473-X_8. ISBN 978-3-540-43869-4. https://link.springer.com/content/pdf/10.1007%2F3-540-45473-X_8.pdf.
- ↑ Jutla, Charanjit S. (May 2001). "Encryption Modes with Almost Free Message Integrity". Eurocrypt 2001. 2045. Springer. doi:10.1007/3-540-44987-6_32. https://iacr.org/archive/eurocrypt2001/20450525.pdf.
- ↑ Template:Cite tech report
- ↑ Whiting, D.; Housley, R.; Ferguson, N. (September 2003), Counter with CBC-MAC (CCM), IETF, doi:10.17487/RFC3610, RFC 3610, https://tools.ietf.org/html/rfc3610
- ↑ Harkins, Dan (October 2008). "Synthetic Initialization Vector (SIV) Authenticated Encryption Using the Advanced Encryption Standard (AES)". https://tools.ietf.org/html/rfc5297.
- ↑ Gueron, S. (April 2019), AES-GCM-SIV: Nonce Misuse-Resistant Authenticated Encryption, IETF, doi:10.17487/RFC8452, RFC 8452, https://tools.ietf.org/html/rfc8452, retrieved August 14, 2019
- ↑ Gueron, Shay; Langley, Adam; Lindell, Yehuda (14 Dec 2018). "AES-GCM-SIV: Specification and Analysis". Cryptology ePrint Archive Report (2017/168). https://eprint.iacr.org/2017/168. Retrieved 19 October 2020.
- ↑ "Recommendation for Block Cipher Modes of Operation". NIST. p. 9. http://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-38a.pdf.
- ↑ Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (2018). Handbook of Applied Cryptography. CRC Press. p. 228. ISBN 9780429881329. https://books.google.com/books?id=YyCyDwAAQBAJ.
- ↑ Dam, Kenneth W.; Lin, Herbert S. (1996). Cryptography's Role in Securing the Information Society. National Academies Press. p. 132. ISBN 9780309054751. https://books.google.com/books?id=H8OaAgAAQBAJ.
- ↑ Schneier, Bruce (2015). Applied Cryptography: Protocols, Algorithms and Source Code in C. John Wiley & Sons. p. 208. ISBN 9781119096726. https://books.google.com/books?id=VjC9BgAAQBAJ.
- ↑ William F. Ehrsam, Carl H. W. Meyer, John L. Smith, Walter L. Tuchman, "Message verification and transmission error detection by block chaining", US Patent 4074066, 1976.
- ↑ "The Transport Layer Security (TLS) Protocol Version 1.1". p. 20. http://www.ietf.org/rfc/rfc4346.txt.
- ↑ "Kryptographie FAQ: Frage 84: What are the Counter and PCBC Modes?". http://www.iks-jena.de/mitarb/lutz/security/cryptfaq/q84.html.
- ↑ Kaufman, C.; Perlman, R.; Speciner, M. (2002). Network Security (2nd ed.). Upper Saddle River, NJ: Prentice Hall. p. 319. ISBN 0130460192.
- ↑ Kohl, J. (1990). "The Use of Encryption in Kerberos for Network Authentication". Proceedings, Crypto '89. Berlin: Springer. ISBN 0387973176. http://dsns.csie.nctu.edu.tw/research/crypto/HTML/PDF/C89/35.PDF.
- ↑ 28.0 28.1 (NIST), Author: Morris Dworkin (2001). SP 800-38A, Recommendation for Block Cipher Modes of Operation: Methods and Techniques. doi:10.6028/NIST.SP.800-38A. http://csrc.nist.gov/publications/nistpubs/800-38a/sp800-38a.pdf. Retrieved 28 April 2018.
- ↑ Davies, D. W.; Parkin, G. I. P. (1983). "The average cycle size of the key stream in output feedback encipherment". Advances in Cryptology, Proceedings of CRYPTO 82. New York: Plenum Press. pp. 263–282. ISBN 0306413663.
- ↑ Jueneman, Robert R. (1983). "Analysis of certain aspects of output feedback mode". Advances in Cryptology, Proceedings of CRYPTO 82. New York: Plenum Press. pp. 99–127. ISBN 0306413663.
- ↑ 31.0 31.1 Lipmaa, Helger; Wagner, David; Rogaway, Phillip (2000). "Comments to NIST concerning AES Modes of Operations: CTR-Mode Encryption". http://csrc.nist.gov/groups/ST/toolkit/BCM/documents/proposedmodes/ctr/ctr-spec.pdf.
- ↑ Ferguson, Niels; Schneier, Bruce; Kohno, Tadayoshi (2010). Cryptography Engineering. p. 71.
- ↑ "Basic Block Cipher Modes". http://www.quadibloc.com/crypto/co040601.htm.
- ↑ "Cryptography I". https://www.coursera.org/learn/crypto.
- ↑ "Modes Development – Block Cipher Techniques – CSRC". Computer Security Division, Information Technology Laboratory, National Institute of Standards and Technology, U.S. Department of Commerce. 4 January 2017. http://csrc.nist.gov/groups/ST/toolkit/BCM/modes_development.html.
 |  |
