Kendall rank correlation coefficient

Short description: Statistic for rank correlation

In statistics, the Kendall rank correlation coefficient, commonly referred to as Kendall's τ coefficient (after the Greek letter τ, tau), is a statistic used to measure the ordinal association between two measured quantities. A τ test is a non-parametric hypothesis test for statistical dependence based on the τ coefficient. It is a measure of rank correlation: the similarity of the orderings of the data when ranked by each of the quantities. It is named after Maurice Kendall, who developed it in 1938, though Gustav Fechner had proposed a similar measure in the context of time series in 1897.

Intuitively, the Kendall correlation between two variables will be high when observations have a similar (or identical for a correlation of 1) rank (i.e. relative position label of the observations within the variable: 1st, 2nd, 3rd, etc.) between the two variables, and low when observations have a dissimilar (or fully different for a correlation of −1) rank between the two variables.

Both Kendall's [math]\displaystyle{ \tau }[/math] and Spearman's [math]\displaystyle{ \rho }[/math] can be formulated as special cases of a more general correlation coefficient. Its notions of concordance and discordance also appear in other areas of statistics, like the Rand index in cluster analysis.

Definition

All points in the gray area are concordant and all points in the white area are discordant with respect to point [math]\displaystyle{ (X_1, Y_1) }[/math]. With [math]\displaystyle{ n=30 }[/math] points, there are a total of [math]\displaystyle{ \binom{30}{2} = 435 }[/math] possible point pairs. In this example there are 395 concordant point pairs and 40 discordant point pairs, leading to a Kendall rank correlation coefficient of 0.816.

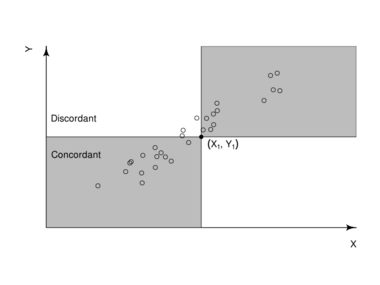
Let [math]\displaystyle{ (x_1,y_1), ..., (x_n,y_n) }[/math] be a set of observations of the joint random variables X and Y, such that all the values of ([math]\displaystyle{ x_i }[/math]) and ([math]\displaystyle{ y_i }[/math]) are unique (ties are neglected for simplicity). Any pair of observations [math]\displaystyle{ (x_i,y_i) }[/math] and [math]\displaystyle{ (x_j,y_j) }[/math], where [math]\displaystyle{ i \lt j }[/math], are said to be concordant if the sort order of [math]\displaystyle{ (x_i,x_j) }[/math] and [math]\displaystyle{ (y_i,y_j) }[/math] agrees: that is, if either both [math]\displaystyle{ x_i\gt x_j }[/math] and [math]\displaystyle{ y_i\gt y_j }[/math] holds or both [math]\displaystyle{ x_i\lt x_j }[/math] and [math]\displaystyle{ y_i\lt y_j }[/math]; otherwise they are said to be discordant.

The Kendall τ coefficient is defined as:

[math]\displaystyle{ \tau = \frac{(\text{number of concordant pairs}) - (\text{number of discordant pairs})}{ (\text{number of pairs}) } = 1- \frac{2 (\text{number of discordant pairs})}{ {n \choose 2} } . }[/math]

where [math]\displaystyle{ {n \choose 2} = {n (n-1) \over 2} }[/math] is the binomial coefficient for the number of ways to choose two items from n items.

The number of discordant pairs is equal to the inversion number that permutes the y-sequence into the same order as the x-sequence.

Properties

The denominator is the total number of pair combinations, so the coefficient must be in the range −1 ≤ τ ≤ 1.

• If the agreement between the two rankings is perfect (i.e., the two rankings are the same) the coefficient has value 1.
• If the disagreement between the two rankings is perfect (i.e., one ranking is the reverse of the other) the coefficient has value −1.
• If X and Y are independent and not constant, then the expectation of the coefficient is zero.
• An explicit expression for Kendall's rank coefficient is [math]\displaystyle{ \tau= \frac{2}{n(n-1)}\sum_{i\lt j} \sgn(x_i-x_j)\sgn(y_i-y_j) }[/math].

Hypothesis test

The Kendall rank coefficient is often used as a test statistic in a statistical hypothesis test to establish whether two variables may be regarded as statistically dependent. This test is non-parametric, as it does not rely on any assumptions on the distributions of X or Y or the distribution of (X,Y).

Under the null hypothesis of independence of X and Y, the sampling distribution of τ has an expected value of zero. The precise distribution cannot be characterized in terms of common distributions, but may be calculated exactly for small samples; for larger samples, it is common to use an approximation to the normal distribution, with mean zero and variance [math]\displaystyle{ 2(2n+5)/9n (n-1) }[/math].

The following proof is from Valz & McLeod (1990; 1995).

Proof

Proof

WLOG, we reorder the data pairs, so that [math]\displaystyle{ x_1 \lt x_2 \lt \cdots \lt x_n }[/math]. By assumption of independence, the order of [math]\displaystyle{ y_1, ..., y_n }[/math] is a permutation sampled uniformly at random from [math]\displaystyle{ S_n }[/math], the permutation group on [math]\displaystyle{ 1:n }[/math].

For each permutation, its unique [math]\displaystyle{ l }[/math] inversion code is [math]\displaystyle{ l_0l_1\cdots l_{n-1} }[/math] such that each [math]\displaystyle{ l_i }[/math] is in the range [math]\displaystyle{ 0:i }[/math]. Sampling a permutation uniformly is equivalent to sampling a [math]\displaystyle{ l }[/math]-inversion code uniformly, which is equivalent to sampling each [math]\displaystyle{ l_i }[/math] uniformly and independently.

Then we have [math]\displaystyle{ \begin{aligned} E[\tau_A^2] &= E\left[\left(1-\frac{4\sum_i l_i}{n(n-1)}\right)^2\right] \\ &= 1 - \frac{8}{n(n-1)}\sum_i E[l_i] + \frac{16}{n^2(n-1)^2}\sum_{ij} E[l_il_j] \\ &= 1 - \frac{8}{n(n-1)}\sum_i E[l_i] + \frac{16}{n^2(n-1)^2} \left(\sum_{ij} E[l_i]E[l_j] + \sum_i V[l_i] \right) \\ &= 1 - \frac{8}{n(n-1)}\sum_i E[l_i] +\frac{16}{n^2(n-1)^2} \sum_{ij} E[l_i]E[l_j] + \frac{16}{n^2(n-1)^2} \left( \sum_i V[l_i] \right) \\ &=\left(1-\frac{4\sum_i E[l_i]}{n(n-1)}\right)^2 + \frac{16}{n^2(n-1)^2} \left( \sum_i V[l_i] \right) \end{aligned} }[/math]

The first term is just [math]\displaystyle{ E[\tau_A]^2 = 0 }[/math]. The second term can be calculated by noting that [math]\displaystyle{ l_i }[/math] is a uniform random variable on [math]\displaystyle{ 0:i }[/math], so [math]\displaystyle{ E[l_i] = \frac i2 }[/math] and [math]\displaystyle{ E[l_i^2] = \frac{0^2+\cdots + i^2}{i+1} = \frac{i(2i+1)}6 }[/math], then using the sum of squares formula again.

Asymptotic normality — At the [math]\displaystyle{ n\to \infty }[/math] limit, [math]\displaystyle{ z_A = \frac{\tau_A}{\sqrt{Var[\tau_A]}} = {n_C - n_D \over \sqrt{n(n-1)(2n+5)/18} } }[/math] converges in distribution to the standard normal distribution.

Proof

Use a result from A class of statistics with asymptotically normal distribution Hoeffding (1948).

Case of standard normal distributions

If [math]\displaystyle{ (x_1, y_1), (x_2, y_2), ..., (x_n, y_n) }[/math] are IID samples from the same jointly normal distribution with a known Pearson correlation coefficient [math]\displaystyle{ r }[/math], then the expectation of Kendall rank correlation has a closed-form formula.

Greiner’s equality — If [math]\displaystyle{ X, Y }[/math] are jointly normal, with correlation [math]\displaystyle{ r }[/math], then [math]\displaystyle{ r = \sin{\left(\frac\pi 2 E[\tau_A]\right)} }[/math]

The name is credited to Richard Greiner (1909) by P. A. P. Moran.

Proof

Proof

Define the following quantities.

• [math]\displaystyle{ A^+ := \{(\Delta x, \Delta y) : \Delta x \Delta y \gt 0\} }[/math]
• [math]\displaystyle{ \Delta_{i,j} := (x_i - x_j , y_i - y_j) }[/math] is a point in [math]\displaystyle{ \R^2 }[/math].

In the notation, we see that the number of concordant pairs, [math]\displaystyle{ n_C }[/math], is equal to the number of [math]\displaystyle{ \Delta_{i, j} }[/math] that fall in the subset [math]\displaystyle{ A^+ }[/math]. That is, [math]\displaystyle{ n_C = \sum_{1 \leq i \lt j \leq n} 1_{\Delta_{i,j} \in A^+} }[/math].

Thus, [math]\displaystyle{ E[\tau_A] = \frac{4}{n(n-1)}E[n_C] - 1 = \frac{4}{n(n-1)}\sum_{1 \leq i \lt j \leq n} Pr(\Delta_{i,j} \in A^+) - 1 }[/math]

Since each [math]\displaystyle{ (x_i, y_i) }[/math] is an IID sample of the jointly normal distribution, the pairing does not matter, so each term in the summation is exactly the same, and so [math]\displaystyle{ E[\tau_A] = 2 Pr(\Delta_{1,2} \in A^+) - 1 }[/math] and it remains to calculate the probability. We perform this by repeated affine transforms.

First normalize [math]\displaystyle{ X, Y }[/math] by subtracting the mean and dividing the standard deviation. This does not change [math]\displaystyle{ \tau_A }[/math]. This gives us [math]\displaystyle{ \begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} 1 & r \\ r & 1 \end{bmatrix}^{1/2} \begin{bmatrix} z \\ w \end{bmatrix} }[/math] where [math]\displaystyle{ (Z, W) }[/math] is sampled from the standard normal distribution on [math]\displaystyle{ \R^2 }[/math].

Thus, [math]\displaystyle{ \Delta_{1,2} = \sqrt 2\begin{bmatrix} 1 & r \\ r & 1 \end{bmatrix}^{1/2} \begin{bmatrix} (z_1-z_2)/\sqrt{2} \\ (w_1-w_2)/\sqrt{2} \end{bmatrix} }[/math] where the vector [math]\displaystyle{ \begin{bmatrix} (z_1-z_2)/\sqrt{2} \\ (w_1-w_2)/\sqrt{2} \end{bmatrix} }[/math] is still distributed as the standard normal distribution on [math]\displaystyle{ \R^2 }[/math]. It remains to perform some unenlightening tedious matrix exponentiations and trigonometry, which can be skipped over.

Thus, [math]\displaystyle{ \Delta_{1,2} \in A^+ }[/math] iff [math]\displaystyle{ \begin{bmatrix} (z_1-z_2)/\sqrt{2} \\ (w_1-w_2)/\sqrt{2} \end{bmatrix} \in \frac{1}{\sqrt 2}\begin{bmatrix} 1 & r \\ r & 1 \end{bmatrix}^{-1/2} A^+ = \frac{1}{2\sqrt 2} \begin{bmatrix} \frac{1}{\sqrt{1+r}}+ \frac{1}{\sqrt{1-r}} & \frac{1}{\sqrt{1+r}} - \frac{1}{\sqrt{1-r}} \\ \frac{1}{\sqrt{1+r}} - \frac{1}{\sqrt{1-r}} & \frac{1}{\sqrt{1+r}} + \frac{1}{\sqrt{1-r}} \end{bmatrix}A^+ }[/math] where the subset on the right is a “squashed” version of two quadrants. Since the standard normal distribution is rotationally symmetric, we need only calculate the angle spanned by each squashed quadrant.

The first quadrant is the sector bounded by the two rays [math]\displaystyle{ (1, 0), (0, 1) }[/math]. It is transformed to the sector bounded by the two rays [math]\displaystyle{ (\frac{1}{\sqrt{1+r}}+ \frac{1}{\sqrt{1-r}}, \frac{1}{\sqrt{1+r}} - \frac{1}{\sqrt{1-r}}) }[/math] and [math]\displaystyle{ (\frac{1}{\sqrt{1+r}} - \frac{1}{\sqrt{1-r}}, \frac{1}{\sqrt{1+r}}+ \frac{1}{\sqrt{1-r}}) }[/math]. They respectively make angle [math]\displaystyle{ \theta }[/math] with the horizontal and vertical axis, where [math]\displaystyle{ \theta = \arctan\frac{\frac{1}{\sqrt{1+r}} - \frac{1}{\sqrt{1-r}}}{\frac{1}{\sqrt{1+r}}+ \frac{1}{\sqrt{1-r}}} }[/math]

Together, the two transformed quadrants span an angle of [math]\displaystyle{ \pi + 4\theta }[/math], so [math]\displaystyle{ Pr(\Delta_{1,2} \in A^+) = \frac{\pi + 4\theta}{2\pi} }[/math] and therefore
[math]\displaystyle{ \sin{\left(\frac\pi 2 E[\tau_A]\right)} = \sin(2\theta) = r }[/math]

Accounting for ties

A pair [math]\displaystyle{ \{ (x_{i},y_{i}),(x_{j},y_{j}) \} }[/math] is said to be tied if and only if [math]\displaystyle{ x_{i} = x_{j} }[/math] or [math]\displaystyle{ y_{i} = y_{j} }[/math]; a tied pair is neither concordant nor discordant. When tied pairs arise in the data, the coefficient may be modified in a number of ways to keep it in the range [−1, 1]:

Tau-a

The Tau-a statistic tests the strength of association of the cross tabulations. Both variables have to be ordinal. Tau-a will not make any adjustment for ties. It is defined as:

[math]\displaystyle{ \tau_A = \frac{n_c-n_d}{n_0} }[/math]

where n_c, n_d and n₀ are defined as in the next section.

Tau-b

The Tau-b statistic, unlike Tau-a, makes adjustments for ties. Values of Tau-b range from −1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.

The Kendall Tau-b coefficient is defined as:

[math]\displaystyle{ \tau_B = \frac{n_c-n_d}{\sqrt{(n_0-n_1)(n_0-n_2)}} }[/math]

where

[math]\displaystyle{ \begin{align} n_0 & = n(n-1)/2\\ n_1 & = \sum_i t_i (t_i-1)/2 \\ n_2 & = \sum_j u_j (u_j-1)/2 \\ n_c & = \text{Number of concordant pairs} \\ n_d & = \text{Number of discordant pairs} \\ t_i & = \text{Number of tied values in the } i^\text{th} \text{ group of ties for the first quantity} \\ u_j & = \text{Number of tied values in the } j^\text{th} \text{ group of ties for the second quantity} \end{align} }[/math]

A simple algorithm developed in BASIC computes Tau-b coefficient using an alternative formula.

Be aware that some statistical packages, e.g. SPSS, use alternative formulas for computational efficiency, with double the 'usual' number of concordant and discordant pairs.

Tau-c

Tau-c (also called Stuart-Kendall Tau-c) is more suitable than Tau-b for the analysis of data based on non-square (i.e. rectangular) contingency tables. So use Tau-b if the underlying scale of both variables has the same number of possible values (before ranking) and Tau-c if they differ. For instance, one variable might be scored on a 5-point scale (very good, good, average, bad, very bad), whereas the other might be based on a finer 10-point scale.

The Kendall Tau-c coefficient is defined as:

[math]\displaystyle{ \tau_C = \frac{2 (n_c-n_d)}{n^2 \frac{(m-1)}{m}} = \tau_A \frac{n-1}{n} \frac{m}{m-1} }[/math]

where

[math]\displaystyle{ \begin{align} n_c & = \text{Number of concordant pairs} \\ n_d & = \text{Number of discordant pairs} \\ r & = \text{Number of rows} \\ c & = \text{Number of columns} \\ m & = \min(r, c) \end{align} }[/math]

Significance tests

When two quantities are statistically dependent, the distribution of [math]\displaystyle{ \tau }[/math] is not easily characterizable in terms of known distributions. However, for [math]\displaystyle{ \tau_A }[/math] the following statistic, [math]\displaystyle{ z_A }[/math], is approximately distributed as a standard normal when the variables are statistically independent:

[math]\displaystyle{ z_A = {n_c - n_d \over \sqrt{\frac{1}{18}v_0} } }[/math]

where [math]\displaystyle{ v_0 = n(n-1)(2n+5) }[/math].

Thus, to test whether two variables are statistically dependent, one computes [math]\displaystyle{ z_A }[/math], and finds the cumulative probability for a standard normal distribution at [math]\displaystyle{ -|z_A| }[/math]. For a 2-tailed test, multiply that number by two to obtain the p-value. If the p-value is below a given significance level, one rejects the null hypothesis (at that significance level) that the quantities are statistically independent.

Numerous adjustments should be added to [math]\displaystyle{ z_A }[/math] when accounting for ties. The following statistic, [math]\displaystyle{ z_B }[/math], has the same distribution as the [math]\displaystyle{ \tau_B }[/math] distribution, and is again approximately equal to a standard normal distribution when the quantities are statistically independent:

[math]\displaystyle{ z_B = {n_c - n_d \over \sqrt{ v } } }[/math]

where

[math]\displaystyle{ \begin{array}{ccl} v & = & \frac{1}{18} v_0 - (v_t + v_u)/18 + (v_1 + v_2) \\ v_0 & = & n (n-1) (2n+5) \\ v_t & = & \sum_i t_i (t_i-1) (2 t_i+5)\\ v_u & = & \sum_j u_j (u_j-1)(2 u_j+5) \\ v_1 & = & \sum_i t_i (t_i-1) \sum_j u_j (u_j-1) / (2n(n-1)) \\ v_2 & = & \sum_i t_i (t_i-1) (t_i-2) \sum_j u_j (u_j-1) (u_j-2) / (9 n (n-1) (n-2)) \end{array} }[/math]

This is sometimes referred to as the Mann-Kendall test.

Algorithms

The direct computation of the numerator [math]\displaystyle{ n_c - n_d }[/math], involves two nested iterations, as characterized by the following pseudocode:

numer := 0
for i := 2..N do
    for j := 1..(i − 1) do
        numer := numer + sign(x[i] − x[j]) × sign(y[i] − y[j])
return numer

Although quick to implement, this algorithm is [math]\displaystyle{ O(n^2) }[/math] in complexity and becomes very slow on large samples. A more sophisticated algorithm built upon the Merge Sort algorithm can be used to compute the numerator in [math]\displaystyle{ O(n \cdot \log{n}) }[/math] time.

Begin by ordering your data points sorting by the first quantity, [math]\displaystyle{ x }[/math], and secondarily (among ties in [math]\displaystyle{ x }[/math]) by the second quantity, [math]\displaystyle{ y }[/math]. With this initial ordering, [math]\displaystyle{ y }[/math] is not sorted, and the core of the algorithm consists of computing how many steps a Bubble Sort would take to sort this initial [math]\displaystyle{ y }[/math]. An enhanced Merge Sort algorithm, with [math]\displaystyle{ O(n \log n) }[/math] complexity, can be applied to compute the number of swaps, [math]\displaystyle{ S(y) }[/math], that would be required by a Bubble Sort to sort [math]\displaystyle{ y_i }[/math]. Then the numerator for [math]\displaystyle{ \tau }[/math] is computed as:

[math]\displaystyle{ n_c-n_d = n_0 - n_1 - n_2 + n_3 - 2 S(y), }[/math]

where [math]\displaystyle{ n_3 }[/math] is computed like [math]\displaystyle{ n_1 }[/math] and [math]\displaystyle{ n_2 }[/math], but with respect to the joint ties in [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math].

A Merge Sort partitions the data to be sorted, [math]\displaystyle{ y }[/math] into two roughly equal halves, [math]\displaystyle{ y_\mathrm{left} }[/math] and [math]\displaystyle{ y_\mathrm{right} }[/math], then sorts each half recursive, and then merges the two sorted halves into a fully sorted vector. The number of Bubble Sort swaps is equal to:

[math]\displaystyle{ S(y) = S(y_\mathrm{left}) + S(y_\mathrm{right}) + M(Y_\mathrm{left},Y_\mathrm{right}) }[/math]

where [math]\displaystyle{ Y_\mathrm{left} }[/math] and [math]\displaystyle{ Y_\mathrm{right} }[/math] are the sorted versions of [math]\displaystyle{ y_\mathrm{left} }[/math] and [math]\displaystyle{ y_\mathrm{right} }[/math], and [math]\displaystyle{ M(\cdot,\cdot) }[/math] characterizes the Bubble Sort swap-equivalent for a merge operation. [math]\displaystyle{ M(\cdot,\cdot) }[/math] is computed as depicted in the following pseudo-code:

function M(L[1..n], R[1..m]) is
    i := 1
    j := 1
    nSwaps := 0
    while i ≤ n and j ≤ m do
        if R[j] < L[i] then
            nSwaps := nSwaps + n − i + 1
            j := j + 1
        else
            i := i + 1
    return nSwaps

A side effect of the above steps is that you end up with both a sorted version of [math]\displaystyle{ x }[/math] and a sorted version of [math]\displaystyle{ y }[/math]. With these, the factors [math]\displaystyle{ t_i }[/math] and [math]\displaystyle{ u_j }[/math] used to compute [math]\displaystyle{ \tau_B }[/math] are easily obtained in a single linear-time pass through the sorted arrays.

Software Implementations

• R implements the test for [math]\displaystyle{ \tau_B }[/math] cor.test(x, y, method = "kendall") in its "stats" package (also cor(x, y, method = "kendall") will work, but the latter does not return the p-value). All three versions of the coefficient are available in the "DescTools" package along with the confidence intervals: KendallTauA(x,y,conf.level=0.95) for [math]\displaystyle{ \tau_A }[/math], KendallTauB(x,y,conf.level=0.95) for [math]\displaystyle{ \tau_B }[/math], StuartTauC(x,y,conf.level=0.95) for [math]\displaystyle{ \tau_C }[/math].
• For Python, the SciPy library implements the computation of [math]\displaystyle{ \tau_B }[/math] in scipy.stats.kendalltau

See also

• Correlation
• Kendall tau distance
• Kendall's W
• Spearman's rank correlation coefficient
• Goodman and Kruskal's gamma
• Theil–Sen estimator
• Mann–Whitney U test - it is equivalent to Kendall's tau correlation coefficient if one of the variables is binary.

Further reading

• Abdi, H. (2007). "Kendall rank correlation". in Salkind, N.J.. Encyclopedia of Measurement and Statistics. Thousand Oaks (CA): Sage. http://www.utdallas.edu/~herve/Abdi-KendallCorrelation2007-pretty.pdf. 
• Daniel, Wayne W. (1990). "Kendall's tau". Applied Nonparametric Statistics (2nd ed.). Boston: PWS-Kent. pp. 365–377. ISBN 978-0-534-91976-4. https://books.google.com/books?id=0hPvAAAAMAAJ&pg=PA365. 
• Kendall, Maurice; Gibbons, Jean Dickinson (1990). Rank Correlation Methods. Charles Griffin Book Series (5th ed.). Oxford: Oxford University Press. ISBN 978-0195208375. https://archive.org/details/rankcorrelationm0000kend. 
• Bonett, Douglas G.; Wright, Thomas A. (2000). "Sample size requirements for estimating Pearson, Kendall, and Spearman correlations". Psychometrika 65 (1): 23–28. doi:10.1007/BF02294183. 

External links

• Tied rank calculation
• Software for computing Kendall's tau on very large datasets
• Online software: computes Kendall's tau rank correlation

de:Rangkorrelationskoeffizient#Kendalls Tau