Alternated hexagonal tiling honeycomb
| Alternated hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb Semiregular honeycomb |
| Schläfli symbols | h{6,3,3} s{3,6,3} 2s{6,3,6} 2s{6,3[3]} s{3[3,3]} |
| Coxeter diagrams | |
| Cells | {3,3} {3[3]} |
| Faces | triangle {3} |
| Vertex figure | truncated tetrahedron |
| Coxeter groups | [math]\displaystyle{ {\overline{P}}_3 }[/math], [3,3[3]] 1/2 [math]\displaystyle{ {\overline{V}}_3 }[/math], [6,3,3] 1/2 [math]\displaystyle{ {\overline{Y}}_3 }[/math], [3,6,3] 1/2 [math]\displaystyle{ {\overline{Z}}_3 }[/math], [6,3,6] 1/2 [math]\displaystyle{ {\overline{VP}}_3 }[/math], [6,3[3]] 1/2 [math]\displaystyle{ {\overline{PP}}_3 }[/math], [3[3,3]] |
| Properties | Vertex-transitive, edge-transitive, quasiregular |
In three-dimensional hyperbolic geometry, the alternated hexagonal tiling honeycomb, h{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() , is a semiregular tessellation with tetrahedron and triangular tiling cells arranged in an octahedron vertex figure. It is named after its construction, as an alteration of a hexagonal tiling honeycomb.
, is a semiregular tessellation with tetrahedron and triangular tiling cells arranged in an octahedron vertex figure. It is named after its construction, as an alteration of a hexagonal tiling honeycomb.
A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
Symmetry constructions
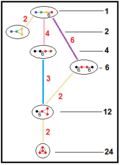
It has five alternated constructions from reflectional Coxeter groups all with four mirrors and only the first being regular: ![]()
![]()
![]()
![]()
![]()
![]()
![]() [6,3,3],
[6,3,3], ![]()
![]()
![]()
![]()
![]()
![]()
![]() [3,6,3],
[3,6,3], ![]()
![]()
![]()
![]()
![]()
![]()
![]() [6,3,6],
[6,3,6], ![]()
![]()
![]()
![]()
![]() [6,3[3]] and [3[3,3]]
[6,3[3]] and [3[3,3]] ![]()
![]()
![]() , having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)*] (remove 3 mirrors, index 24 subgroup); [3,6,3*] or [3*,6,3] (remove 2 mirrors, index 6 subgroup); [1+,6,3,6,1+] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3[3,3]]. The ringed Coxeter diagrams are
, having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)*] (remove 3 mirrors, index 24 subgroup); [3,6,3*] or [3*,6,3] (remove 2 mirrors, index 6 subgroup); [1+,6,3,6,1+] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3[3,3]]. The ringed Coxeter diagrams are ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() and
and ![]()
![]()
![]() , representing different types (colors) of hexagonal tilings in the Wythoff construction.
, representing different types (colors) of hexagonal tilings in the Wythoff construction.
Related honeycombs
The alternated hexagonal tiling honeycomb has 3 related forms: the cantic hexagonal tiling honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ; the runcic hexagonal tiling honeycomb,
; the runcic hexagonal tiling honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ; and the runcicantic hexagonal tiling honeycomb,
; and the runcicantic hexagonal tiling honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Cantic hexagonal tiling honeycomb
| Cantic hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | h2{6,3,3} |
| Coxeter diagrams | |
| Cells | r{3,3} t{3,3} 40px h2{6,3} |
| Faces | triangle {3} hexagon {6} |
| Vertex figure | 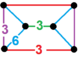 wedge |
| Coxeter groups | [math]\displaystyle{ {\overline{P}}_3 }[/math], [3,3[3]] |
| Properties | Vertex-transitive |
The cantic hexagonal tiling honeycomb, h2{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() , is composed of octahedron, truncated tetrahedron, and trihexagonal tiling facets, with a wedge vertex figure.
, is composed of octahedron, truncated tetrahedron, and trihexagonal tiling facets, with a wedge vertex figure.
Runcic hexagonal tiling honeycomb
| Runcic hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | h3{6,3,3} |
| Coxeter diagrams | |
| Cells | {3,3} {}x{3} 40px rr{3,3} 40px {3[3]} |
| Faces | triangle {3} square {4} hexagon {6} |
| Vertex figure | 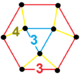 triangular cupola |
| Coxeter groups | [math]\displaystyle{ {\overline{P}}_3 }[/math], [3,3[3]] |
| Properties | Vertex-transitive |
The runcic hexagonal tiling honeycomb, h3{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() , has tetrahedron, triangular prism, cuboctahedron, and triangular tiling facets, with a triangular cupola vertex figure.
, has tetrahedron, triangular prism, cuboctahedron, and triangular tiling facets, with a triangular cupola vertex figure.
Runcicantic hexagonal tiling honeycomb
| Runcicantic hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | h2,3{6,3,3} |
| Coxeter diagrams | |
| Cells | t{3,3} {}x{3} 40px tr{3,3} 40px h2{6,3} |
| Faces | triangle {3} square {4} hexagon {6} |
| Vertex figure | 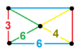 rectangular pyramid |
| Coxeter groups | [math]\displaystyle{ {\overline{P}}_3 }[/math], [3,3[3]] |
| Properties | Vertex-transitive |
The runcicantic hexagonal tiling honeycomb, h2,3{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() , has truncated tetrahedron, triangular prism, truncated octahedron, and trihexagonal tiling facets, with a rectangular pyramid vertex figure.
, has truncated tetrahedron, triangular prism, truncated octahedron, and trihexagonal tiling facets, with a rectangular pyramid vertex figure.
See also
- Convex uniform honeycombs in hyperbolic space
- Regular tessellations of hyperbolic 3-space
- Paracompact uniform honeycombs
- Semiregular honeycomb
- Hexagonal tiling honeycomb
References
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN:0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN:0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space ) Table III
- Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN:0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353 [1] [2]
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H3: p130. [3]
 |