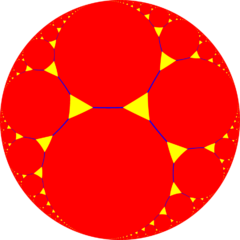
Hexagonal tiling honeycomb

Hexagonal tiling honeycomb
Perspective projection view within Poincaré disk model
Type	Hyperbolic regular honeycomb Paracompact uniform honeycomb
Schläfli symbols	{6,3,3} t{3,6,3} 2t{6,3,6} 2t{6,3[3]} t{3[3,3]}
Coxeter diagrams	↔ ↔ ↔ ↔
Cells	{6,3}
Faces	hexagon {6}
Edge figure	triangle {3}
Vertex figure	tetrahedron {3,3}
Dual	Order-6 tetrahedral honeycomb
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6] [math]\displaystyle{ {\overline{Y}}_3 }[/math], [3,6,3] [math]\displaystyle{ {\overline{Z}}_3 }[/math], [6,3,6] [math]\displaystyle{ {\overline{VP}}_3 }[/math], [6,3[3]] [math]\displaystyle{ {\overline{PP}}_3 }[/math], [3[3,3]]
Properties	Regular

In the field of hyperbolic geometry, the hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere, a surface in hyperbolic space that approaches a single ideal point at infinity.

The Schläfli symbol of the hexagonal tiling honeycomb is {6,3,3}. Since that of the hexagonal tiling is {6,3}, this honeycomb has three such hexagonal tilings meeting at each edge. Since the Schläfli symbol of the tetrahedron is {3,3}, the vertex figure of this honeycomb is a tetrahedron. Thus, four hexagonal tilings meet at each vertex of this honeycomb, six hexagons meet at each vertex, and four edges meet at each vertex.

Images

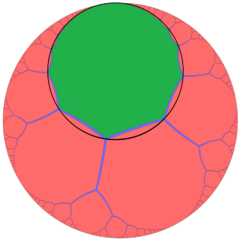
Viewed in perspective outside of a Poincaré disk model, the image above shows one hexagonal tiling cell within the honeycomb, and its mid-radius horosphere (the horosphere incident with edge midpoints). In this projection, the hexagons grow infinitely small towards the infinite boundary, asymptoting towards a single ideal point. It can be seen as similar to the order-3 apeirogonal tiling, {∞,3} of H², with horocycles circumscribing vertices of apeirogonal faces.

{6,3,3}	{∞,3}
One hexagonal tiling cell of the hexagonal tiling honeycomb	An order-3 apeirogonal tiling with a green apeirogon and its horocycle

Symmetry constructions

Subgroup relations

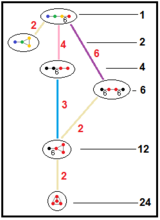
It has a total of five reflectional constructions from five related Coxeter groups all with four mirrors and only the first being regular: [6,3,3], [3,6,3], [6,3,6], [6,3^[3]] and [3^[3,3]] , having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)^*] (remove 3 mirrors, index 24 subgroup); [3,6,3^*] or [3^*,6,3] (remove 2 mirrors, index 6 subgroup); [1⁺,6,3,6,1⁺] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3^[3,3]]. The ringed Coxeter diagrams are , , , and , representing different types (colors) of hexagonal tilings in the Wythoff construction.

Related polytopes and honeycombs

The hexagonal tiling honeycomb is a regular hyperbolic honeycomb in 3-space, and one of 11 which are paracompact.

It is one of 15 uniform paracompact honeycombs in the [6,3,3] Coxeter group, along with its dual, the order-6 tetrahedral honeycomb.

It is part of a sequence of regular polychora, which include the 5-cell {3,3,3}, tesseract {4,3,3}, and 120-cell {5,3,3} of Euclidean 4-space, along with other hyperbolic honeycombs containing tetrahedral vertex figures. It is also part of a sequence of regular honeycombs of the form {6,3,p}, which are each composed of hexagonal tiling cells:

Rectified hexagonal tiling honeycomb

Rectified hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	r{6,3,3} or t1{6,3,3}
Coxeter diagrams	↔
Cells	{3,3} r{6,3} 40px or
Faces	triangle {3} hexagon {6}
Vertex figure	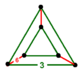triangular prism
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6] [math]\displaystyle{ {\overline{P}}_3 }[/math], [3,3[3]]
Properties	Vertex-transitive, edge-transitive

The rectified hexagonal tiling honeycomb, t₁{6,3,3}, has tetrahedral and trihexagonal tiling facets, with a triangular prism vertex figure. The half-symmetry construction alternates two types of tetrahedra.

Hexagonal tiling honeycomb	Rectified hexagonal tiling honeycomb or
Related H2 tilings
Order-3 apeirogonal tiling	Triapeirogonal tiling or

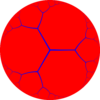
Truncated hexagonal tiling honeycomb

Truncated hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t{6,3,3} or t0,1{6,3,3}
Coxeter diagram
Cells	{3,3} t{6,3}
Faces	triangle {3} dodecagon {12}
Vertex figure	triangular pyramid
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6]
Properties	Vertex-transitive

The truncated hexagonal tiling honeycomb, t_0,1{6,3,3}, has tetrahedral and truncated hexagonal tiling facets, with a triangular pyramid vertex figure.

It is similar to the 2D hyperbolic truncated order-3 apeirogonal tiling, t{∞,3} with apeirogonal and triangle faces:

Bitruncated hexagonal tiling honeycomb

Bitruncated hexagonal tiling honeycomb Bitruncated order-6 tetrahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	2t{6,3,3} or t1,2{6,3,3}
Coxeter diagram	↔
Cells	t{3,3} t{3,6}
Faces	triangle {3} hexagon {6}
Vertex figure	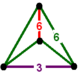digonal disphenoid
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6] [math]\displaystyle{ {\overline{P}}_3 }[/math], [3,3[3]]
Properties	Vertex-transitive

The bitruncated hexagonal tiling honeycomb or bitruncated order-6 tetrahedral honeycomb, t_1,2{6,3,3}, has truncated tetrahedron and hexagonal tiling cells, with a digonal disphenoid vertex figure.

Cantellated hexagonal tiling honeycomb

Cantellated hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	rr{6,3,3} or t0,2{6,3,3}
Coxeter diagram
Cells	r{3,3} rr{6,3} 40px {}×{3}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	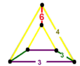wedge
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6]
Properties	Vertex-transitive

The cantellated hexagonal tiling honeycomb, t_0,2{6,3,3}, has octahedron, rhombitrihexagonal tiling, and triangular prism cells, with a wedge vertex figure.

Cantitruncated hexagonal tiling honeycomb

Cantitruncated hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	tr{6,3,3} or t0,1,2{6,3,3}
Coxeter diagram
Cells	t{3,3} tr{6,3} 40px {}×{3}
Faces	triangle {3} square {4} hexagon {6} dodecagon {12}
Vertex figure	mirrored sphenoid
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6]
Properties	Vertex-transitive

The cantitruncated hexagonal tiling honeycomb, t_0,1,2{6,3,3}, has truncated tetrahedron, truncated trihexagonal tiling, and triangular prism cells, with a mirrored sphenoid vertex figure.

Runcinated hexagonal tiling honeycomb

Runcinated hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,3{6,3,3}
Coxeter diagram
Cells	{3,3} {6,3} 40px {}×{6}40px {}×{3}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	irregular triangular antiprism
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6]
Properties	Vertex-transitive

The runcinated hexagonal tiling honeycomb, t_0,3{6,3,3}, has tetrahedron, hexagonal tiling, hexagonal prism, and triangular prism cells, with an irregular triangular antiprism vertex figure.

Runcitruncated hexagonal tiling honeycomb

Runcitruncated hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,1,3{6,3,3}
Coxeter diagram
Cells	rr{3,3} {}x{3} 40px {}x{12} 40px t{6,3}
Faces	triangle {3} square {4} dodecagon {12}
Vertex figure	isosceles-trapezoidal pyramid
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6]
Properties	Vertex-transitive

The runcitruncated hexagonal tiling honeycomb, t_0,1,3{6,3,3}, has cuboctahedron, triangular prism, dodecagonal prism, and truncated hexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure.

Runcicantellated hexagonal tiling honeycomb

Runcicantellated hexagonal tiling honeycomb runcitruncated order-6 tetrahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,2,3{6,3,3}
Coxeter diagram
Cells	t{3,3} {}x{6} 40px rr{6,3}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	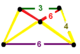isosceles-trapezoidal pyramid
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6]
Properties	Vertex-transitive

The runcicantellated hexagonal tiling honeycomb or runcitruncated order-6 tetrahedral honeycomb, t_0,2,3{6,3,3}, has truncated tetrahedron, hexagonal prism, and rhombitrihexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure.

Omnitruncated hexagonal tiling honeycomb

Omnitruncated hexagonal tiling honeycomb Omnitruncated order-6 tetrahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbol	t0,1,2,3{6,3,3}
Coxeter diagram
Cells	tr{3,3} {}x{6} 40px {}x{12} 40px tr{6,3}
Faces	square {4} hexagon {6} dodecagon {12}
Vertex figure	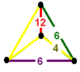irregular tetrahedron
Coxeter groups	[math]\displaystyle{ {\overline{V}}_3 }[/math], [3,3,6]
Properties	Vertex-transitive

The omnitruncated hexagonal tiling honeycomb or omnitruncated order-6 tetrahedral honeycomb, t_0,1,2,3{6,3,3}, has truncated octahedron, hexagonal prism, dodecagonal prism, and truncated trihexagonal tiling cells, with an irregular tetrahedron vertex figure.

See also

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space
• Paracompact uniform honeycombs
• Alternated hexagonal tiling honeycomb

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN:0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN:0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space ) Table III
• Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN:0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
• N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353 [1] [2]
• N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H³: p130. [3]

External links

• John Baez, Visual Insight: {6,3,3} Honeycomb (2014/03/15)
• John Baez, Visual Insight: {6,3,3} Honeycomb in Upper Half Space (2013/09/15)
• John Baez, Visual Insight: Truncated {6,3,3} Honeycomb (2016/12/01)