Proofs of trigonometric identities

Short description: Collection of proofs of equations involving trigonometric functions

There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of right triangles. The proofs given in this article use this definition, and thus apply to non-negative angles not greater than a right angle. For greater and negative angles, see Trigonometric functions.

Other definitions, and therefore other proofs are based on the Taylor series of sine and cosine, or on the differential equation [math]\displaystyle{ f''+f=0 }[/math] to which they are solutions.

Elementary trigonometric identities

Definitions

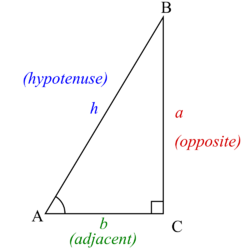
Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle. For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse.

The six trigonometric functions are defined for every real number, except, for some of them, for angles that differ from 0 by a multiple of the right angle (90°). Referring to the diagram at the right, the six trigonometric functions of θ are, for angles smaller than the right angle:

[math]\displaystyle{ \sin \theta = \frac {\mathrm{opposite}}{\mathrm{hypotenuse}} = \frac {a}{h} }[/math]

[math]\displaystyle{ \cos \theta = \frac {\mathrm{adjacent}}{\mathrm{hypotenuse}} = \frac {b}{h} }[/math]

[math]\displaystyle{ \tan \theta = \frac {\mathrm{opposite}}{\mathrm{adjacent}} = \frac {a}{b} }[/math]

[math]\displaystyle{ \cot \theta = \frac {\mathrm{adjacent}}{\mathrm{opposite}} = \frac {b}{a} }[/math]

[math]\displaystyle{ \sec \theta = \frac {\mathrm{hypotenuse}}{\mathrm{adjacent}} = \frac {h}{b} }[/math]

[math]\displaystyle{ \csc \theta = \frac {\mathrm{hypotenuse}}{\mathrm{opposite}} = \frac {h}{a} }[/math]

Ratio identities

In the case of angles smaller than a right angle, the following identities are direct consequences of above definitions through the division identity

[math]\displaystyle{ \frac {a}{b}= \frac {\left(\frac {a}{h}\right)} {\left(\frac {b}{h}\right) }. }[/math]

They remain valid for angles greater than 90° and for negative angles.

[math]\displaystyle{ \tan \theta = \frac{\mathrm{opposite}}{\mathrm{adjacent}} = \frac { \left( \frac{\mathrm{opposite}}{\mathrm{hypotenuse}} \right) } { \left( \frac{\mathrm{adjacent}}{\mathrm{hypotenuse}}\right) } = \frac {\sin \theta} {\cos \theta} }[/math]

[math]\displaystyle{ \cot \theta =\frac{\mathrm{adjacent}}{\mathrm{opposite}} = \frac { \left( \frac{\mathrm{adjacent}}{\mathrm{adjacent}} \right) } { \left( \frac {\mathrm{opposite}}{\mathrm{adjacent}} \right) } = \frac {1}{\tan \theta} = \frac {\cos \theta}{\sin \theta} }[/math]

[math]\displaystyle{ \sec \theta = \frac {1}{\cos \theta} = \frac{\mathrm{hypotenuse}}{\mathrm{adjacent}} }[/math]

[math]\displaystyle{ \csc \theta = \frac {1}{\sin \theta} = \frac{\mathrm{hypotenuse}}{\mathrm{opposite}} }[/math]

[math]\displaystyle{ \tan \theta = \frac{\mathrm{opposite}}{\mathrm{adjacent}} = \frac{\left(\frac{\mathrm{opposite} \times \mathrm{hypotenuse}}{\mathrm{opposite} \times \mathrm{adjacent}} \right) } { \left( \frac {\mathrm{adjacent} \times \mathrm{hypotenuse}} {\mathrm{opposite} \times \mathrm{adjacent} } \right) } = \frac{\left( \frac{\mathrm{hypotenuse}}{\mathrm{adjacent}} \right)} { \left( \frac{\mathrm{hypotenuse}}{\mathrm{opposite}} \right)} = \frac {\sec \theta}{\csc \theta} }[/math]

Or

[math]\displaystyle{ \tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{\left( \frac{1}{\csc \theta} \right) }{\left( \frac{1}{\sec \theta} \right) } = \frac{\left( \frac{\csc \theta \sec \theta}{\csc \theta} \right) }{\left( \frac{\csc \theta \sec \theta}{\sec \theta} \right) } = \frac{\sec \theta}{\csc \theta} }[/math]

[math]\displaystyle{ \cot \theta = \frac {\csc \theta}{\sec \theta} }[/math]

Complementary angle identities

Two angles whose sum is π/2 radians (90 degrees) are complementary. In the diagram, the angles at vertices A and B are complementary, so we can exchange a and b, and change θ to π/2 − θ, obtaining:

[math]\displaystyle{ \sin\left( \pi/2-\theta\right) = \cos \theta }[/math]

[math]\displaystyle{ \cos\left( \pi/2-\theta\right) = \sin \theta }[/math]

[math]\displaystyle{ \tan\left( \pi/2-\theta\right) = \cot \theta }[/math]

[math]\displaystyle{ \cot\left( \pi/2-\theta\right) = \tan \theta }[/math]

[math]\displaystyle{ \sec\left( \pi/2-\theta\right) = \csc \theta }[/math]

[math]\displaystyle{ \csc\left( \pi/2-\theta\right) = \sec \theta }[/math]

Pythagorean identities

Identity 1:

[math]\displaystyle{ \sin^2\theta + \cos^2\theta = 1 }[/math]

The following two results follow from this and the ratio identities. To obtain the first, divide both sides of [math]\displaystyle{ \sin^2\theta + \cos^2\theta = 1 }[/math] by [math]\displaystyle{ \cos^2\theta }[/math]; for the second, divide by [math]\displaystyle{ \sin^2\theta }[/math].

[math]\displaystyle{ \tan^2\theta + 1\ = \sec^2\theta }[/math]

[math]\displaystyle{ \sec^2\theta - \tan^2\theta = 1 }[/math]

Similarly

[math]\displaystyle{ 1\ + \cot^2\theta = \csc^2\theta }[/math]

[math]\displaystyle{ \csc^2\theta - \cot^2\theta = 1 }[/math]

Identity 2:

The following accounts for all three reciprocal functions.

[math]\displaystyle{ \csc^2\theta + \sec^2\theta - \cot^2\theta = 2\ + \tan^2\theta }[/math]

Proof 2:

Refer to the triangle diagram above. Note that [math]\displaystyle{ a^2+b^2=h^2 }[/math] by Pythagorean theorem.

[math]\displaystyle{ \csc^2\theta + \sec^2\theta = \frac{h^2}{a^2} + \frac{h^2}{b^2} = \frac{a^2+b^2}{a^2} + \frac{a^2+b^2}{b^2} = 2\ + \frac{b^2}{a^2} + \frac{a^2}{b^2} }[/math]

Substituting with appropriate functions -

[math]\displaystyle{ 2\ + \frac{b^2}{a^2} + \frac{a^2}{b^2} = 2\ + \tan^2\theta+ \cot^2\theta }[/math]

Rearranging gives:

[math]\displaystyle{ \csc^2\theta + \sec^2\theta - \cot^2\theta = 2\ + \tan^2\theta }[/math]

Angle sum identities

Sine

Illustration of the sum formula.

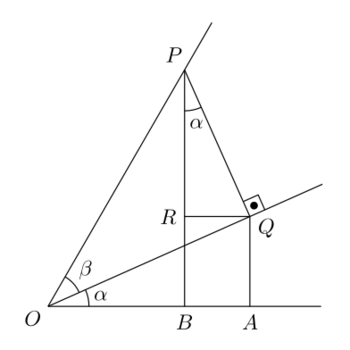
Draw a horizontal line (the x-axis); mark an origin O. Draw a line from O at an angle [math]\displaystyle{ \alpha }[/math] above the horizontal line and a second line at an angle [math]\displaystyle{ \beta }[/math] above that; the angle between the second line and the x-axis is [math]\displaystyle{ \alpha + \beta }[/math].

Place P on the line defined by [math]\displaystyle{ \alpha + \beta }[/math] at a unit distance from the origin.

Let PQ be a line perpendicular to line OQ defined by angle [math]\displaystyle{ \alpha }[/math], drawn from point Q on this line to point P. [math]\displaystyle{ \therefore }[/math] OQP is a right angle.

Let QA be a perpendicular from point A on the x-axis to Q and PB be a perpendicular from point B on the x-axis to P. [math]\displaystyle{ \therefore }[/math] OAQ and OBP are right angles.

Draw R on PB so that QR is parallel to the x-axis.

Now angle [math]\displaystyle{ RPQ = \alpha }[/math] (because [math]\displaystyle{ OQA = \frac{\pi}{2} - \alpha }[/math], making [math]\displaystyle{ RQO = \alpha, RQP = \frac{\pi}{2}-\alpha }[/math], and finally [math]\displaystyle{ RPQ = \alpha }[/math])

[math]\displaystyle{ RPQ = \tfrac{\pi}{2} - RQP = \tfrac{\pi}{2} - (\tfrac{\pi}{2} - RQO) = RQO = \alpha }[/math]

[math]\displaystyle{ OP = 1 }[/math]

[math]\displaystyle{ PQ = \sin \beta }[/math]

[math]\displaystyle{ OQ = \cos \beta }[/math]

[math]\displaystyle{ \frac{AQ}{OQ} = \sin \alpha }[/math], so [math]\displaystyle{ AQ = \sin \alpha \cos \beta }[/math]

[math]\displaystyle{ \frac{PR}{PQ} = \cos \alpha }[/math], so [math]\displaystyle{ PR = \cos \alpha \sin \beta }[/math]

[math]\displaystyle{ \sin (\alpha + \beta) = PB = RB+PR = AQ+PR = \sin \alpha \cos \beta + \cos \alpha \sin \beta }[/math]

By substituting [math]\displaystyle{ -\beta }[/math] for [math]\displaystyle{ \beta }[/math] and using the reflection identities of even and odd functions, we also get:

[math]\displaystyle{ \sin (\alpha - \beta) = \sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta) }[/math]

[math]\displaystyle{ \sin (\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta }[/math]

Cosine

Using the figure above,

[math]\displaystyle{ OP = 1 }[/math]

[math]\displaystyle{ PQ = \sin \beta }[/math]

[math]\displaystyle{ OQ = \cos \beta }[/math]

[math]\displaystyle{ \frac{OA}{OQ} = \cos \alpha }[/math], so [math]\displaystyle{ OA = \cos \alpha \cos \beta }[/math]

[math]\displaystyle{ \frac{RQ}{PQ} = \sin \alpha }[/math], so [math]\displaystyle{ RQ = \sin \alpha \sin \beta }[/math]

[math]\displaystyle{ \cos (\alpha + \beta) = OB = OA-BA = OA-RQ = \cos \alpha \cos \beta\ - \sin \alpha \sin \beta }[/math]

By substituting [math]\displaystyle{ -\beta }[/math] for [math]\displaystyle{ \beta }[/math] and using the reflection identities of even and odd functions, we also get:

[math]\displaystyle{ \cos (\alpha - \beta) = \cos \alpha \cos (-\beta) - \sin \alpha \sin (-\beta), }[/math]

[math]\displaystyle{ \cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta }[/math]

Also, using the complementary angle formulae,

[math]\displaystyle{ \begin{align} \cos (\alpha + \beta) & = \sin\left( \pi/2-(\alpha + \beta)\right) \\ & = \sin\left( (\pi/2-\alpha) - \beta\right) \\ & = \sin\left( \pi/2-\alpha\right) \cos \beta - \cos\left( \pi/2-\alpha\right) \sin \beta \\ & = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \end{align} }[/math]

Tangent and cotangent

From the sine and cosine formulae, we get

[math]\displaystyle{ \tan (\alpha + \beta) = \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)} = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} }[/math]

Dividing both numerator and denominator by [math]\displaystyle{ \cos \alpha \cos \beta }[/math], we get

[math]\displaystyle{ \tan (\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} }[/math]

Subtracting [math]\displaystyle{ \beta }[/math] from [math]\displaystyle{ \alpha }[/math], using [math]\displaystyle{ \tan (- \beta) = -\tan \beta }[/math],

[math]\displaystyle{ \tan (\alpha - \beta) = \frac{\tan \alpha + \tan (-\beta)}{1 - \tan \alpha \tan (-\beta)} = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} }[/math]

Similarly from the sine and cosine formulae, we get

[math]\displaystyle{ \cot (\alpha + \beta) = \frac{\cos (\alpha + \beta)}{\sin (\alpha + \beta)} = \frac{\cos \alpha \cos \beta - \sin \alpha \sin \beta}{\sin \alpha \cos \beta + \cos \alpha \sin \beta} }[/math]

Then by dividing both numerator and denominator by [math]\displaystyle{ \sin \alpha \sin \beta }[/math], we get

[math]\displaystyle{ \cot (\alpha + \beta) = \frac{\cot \alpha \cot \beta - 1}{\cot \alpha + \cot \beta} }[/math]

Or, using [math]\displaystyle{ \cot \theta = \frac{1}{\tan \theta} }[/math],

[math]\displaystyle{ \cot (\alpha + \beta) = \frac{1 - \tan \alpha \tan \beta}{\tan \alpha + \tan \beta} = \frac{\frac{1}{\tan \alpha \tan \beta} - 1}{\frac{1}{\tan \alpha} + \frac{1}{\tan \beta}} = \frac{\cot \alpha \cot \beta - 1}{\cot \alpha + \cot \beta} }[/math]

Using [math]\displaystyle{ \cot (- \beta) = -\cot \beta }[/math],

[math]\displaystyle{ \cot (\alpha - \beta) = \frac{\cot \alpha \cot (-\beta) - 1}{ \cot \alpha + \cot (-\beta) } = \frac{\cot \alpha \cot \beta + 1}{\cot \beta - \cot \alpha} }[/math]

Double-angle identities

From the angle sum identities, we get

[math]\displaystyle{ \sin (2 \theta) = 2 \sin \theta \cos \theta }[/math]

and

[math]\displaystyle{ \cos (2 \theta) = \cos^2 \theta - \sin^2 \theta }[/math]

The Pythagorean identities give the two alternative forms for the latter of these:

[math]\displaystyle{ \cos (2 \theta) = 2 \cos^2 \theta - 1 }[/math]

[math]\displaystyle{ \cos (2 \theta) = 1 - 2 \sin^2 \theta }[/math]

The angle sum identities also give

[math]\displaystyle{ \tan (2 \theta) = \frac{2 \tan \theta}{1 - \tan^2 \theta} = \frac{2}{\cot \theta - \tan \theta} }[/math]

[math]\displaystyle{ \cot (2 \theta) = \frac{\cot^2 \theta - 1}{2 \cot \theta} = \frac{\cot \theta - \tan \theta}{2} }[/math]

It can also be proved using Euler's formula

[math]\displaystyle{ e^{i \varphi}=\cos \varphi +i \sin \varphi }[/math]

Squaring both sides yields

[math]\displaystyle{ e^{i 2\varphi}=(\cos \varphi +i \sin \varphi)^{2} }[/math]

But replacing the angle with its doubled version, which achieves the same result in the left side of the equation, yields

[math]\displaystyle{ e^{i 2\varphi}=\cos 2\varphi +i \sin 2\varphi }[/math]

It follows that

[math]\displaystyle{ (\cos \varphi +i \sin \varphi)^{2}=\cos 2\varphi +i \sin 2\varphi }[/math].

Expanding the square and simplifying on the left hand side of the equation gives

[math]\displaystyle{ i(2 \sin \varphi \cos \varphi) + \cos^2 \varphi - \sin^2 \varphi\ = \cos 2\varphi +i \sin 2\varphi }[/math].

Because the imaginary and real parts have to be the same, we are left with the original identities

[math]\displaystyle{ \cos^2 \varphi - \sin^2 \varphi\ = \cos 2\varphi }[/math],

and also

[math]\displaystyle{ 2 \sin \varphi \cos \varphi = \sin 2\varphi }[/math].

Half-angle identities

The two identities giving the alternative forms for cos 2θ lead to the following equations:

[math]\displaystyle{ \cos \frac{\theta}{2} = \pm\, \sqrt\frac{1 + \cos \theta}{2}, }[/math]

[math]\displaystyle{ \sin \frac{\theta}{2} = \pm\, \sqrt\frac{1 - \cos \theta}{2}. }[/math]

The sign of the square root needs to be chosen properly—note that if 2 $π$ is added to θ, the quantities inside the square roots are unchanged, but the left-hand-sides of the equations change sign. Therefore, the correct sign to use depends on the value of θ.

For the tan function, the equation is:

[math]\displaystyle{ \tan \frac{\theta}{2} = \pm\, \sqrt\frac{1 - \cos \theta}{1 + \cos \theta}. }[/math]

Then multiplying the numerator and denominator inside the square root by (1 + cos θ) and using Pythagorean identities leads to:

[math]\displaystyle{ \tan \frac{\theta}{2} = \frac{\sin \theta}{1 + \cos \theta}. }[/math]

Also, if the numerator and denominator are both multiplied by (1 - cos θ), the result is:

[math]\displaystyle{ \tan \frac{\theta}{2} = \frac{1 - \cos \theta}{\sin \theta}. }[/math]

This also gives:

[math]\displaystyle{ \tan \frac{\theta}{2} = \csc \theta - \cot \theta. }[/math]

Similar manipulations for the cot function give:

[math]\displaystyle{ \cot \frac{\theta}{2} = \pm\, \sqrt\frac{1 + \cos \theta}{1 - \cos \theta} = \frac{1 + \cos \theta}{\sin \theta} = \frac{\sin \theta}{1 - \cos \theta} = \csc \theta + \cot \theta. }[/math]

Miscellaneous – the triple tangent identity

If [math]\displaystyle{ \psi + \theta + \phi = \pi = }[/math] half circle (for example, [math]\displaystyle{ \psi }[/math], [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math] are the angles of a triangle),

[math]\displaystyle{ \tan(\psi) + \tan(\theta) + \tan(\phi) = \tan(\psi)\tan(\theta)\tan(\phi). }[/math]

Proof:^[1]

[math]\displaystyle{ \begin{align} \psi & = \pi - \theta - \phi \\ \tan(\psi) & = \tan(\pi - \theta - \phi) \\ & = - \tan(\theta + \phi) \\ & = \frac{- \tan\theta - \tan\phi}{1 - \tan\theta \tan\phi} \\ & = \frac{\tan\theta + \tan\phi}{\tan\theta \tan\phi - 1} \\ (\tan\theta \tan\phi - 1) \tan\psi & = \tan\theta + \tan\phi \\ \tan\psi \tan\theta \tan\phi - \tan\psi & = \tan\theta + \tan\phi \\ \tan\psi \tan\theta \tan\phi & = \tan\psi + \tan\theta + \tan\phi \\ \end{align} }[/math]

Miscellaneous – the triple cotangent identity

If [math]\displaystyle{ \psi + \theta + \phi = \tfrac{\pi}{2} = }[/math] quarter circle,

[math]\displaystyle{ \cot(\psi) + \cot(\theta) + \cot(\phi) = \cot(\psi)\cot(\theta)\cot(\phi) }[/math].

Proof:

Replace each of [math]\displaystyle{ \psi }[/math], [math]\displaystyle{ \theta }[/math], and [math]\displaystyle{ \phi }[/math] with their complementary angles, so cotangents turn into tangents and vice versa.

Given

[math]\displaystyle{ \psi + \theta + \phi = \tfrac{\pi}{2} }[/math]

[math]\displaystyle{ \therefore (\tfrac{\pi}{2}-\psi) + (\tfrac{\pi}{2}-\theta) + (\tfrac{\pi}{2}-\phi) = \tfrac{3\pi}{2} - (\psi+\theta+\phi) = \tfrac{3\pi}{2} - \tfrac{\pi}{2} = \pi }[/math]

so the result follows from the triple tangent identity.

Sum to product identities

[math]\displaystyle{ \sin \theta \pm \sin \phi = 2 \sin \left ( \frac{\theta\pm \phi}2 \right ) \cos \left ( \frac{\theta\mp \phi}2 \right ) }[/math]
[math]\displaystyle{ \cos \theta + \cos \phi = 2 \cos \left ( \frac{\theta+\phi}2 \right ) \cos \left ( \frac{\theta-\phi}2 \right ) }[/math]
[math]\displaystyle{ \cos \theta - \cos \phi = -2 \sin \left ( \frac{\theta+\phi}2 \right ) \sin \left ( \frac{\theta-\phi}2 \right ) }[/math]

Proof of sine identities

First, start with the sum-angle identities:

[math]\displaystyle{ \sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta }[/math]

[math]\displaystyle{ \sin (\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta }[/math]

By adding these together,

[math]\displaystyle{ \sin (\alpha + \beta) + \sin (\alpha - \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta + \sin \alpha \cos \beta - \cos \alpha \sin \beta = 2 \sin \alpha \cos \beta }[/math]

Similarly, by subtracting the two sum-angle identities,

[math]\displaystyle{ \sin (\alpha + \beta) - \sin (\alpha - \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta - \sin \alpha \cos \beta + \cos \alpha \sin \beta = 2 \cos \alpha \sin \beta }[/math]

Let [math]\displaystyle{ \alpha + \beta = \theta }[/math] and [math]\displaystyle{ \alpha - \beta = \phi }[/math],

[math]\displaystyle{ \therefore \alpha = \frac{\theta + \phi}2 }[/math] and [math]\displaystyle{ \beta = \frac{\theta - \phi}2 }[/math]

Substitute [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math]

[math]\displaystyle{ \sin \theta + \sin \phi = 2 \sin \left( \frac{\theta + \phi}2 \right) \cos \left( \frac{\theta - \phi}2 \right) }[/math]

[math]\displaystyle{ \sin \theta - \sin \phi = 2 \cos \left( \frac{\theta + \phi}2 \right) \sin \left( \frac{\theta - \phi}2 \right) = 2 \sin \left( \frac{\theta - \phi}2 \right) \cos \left( \frac{\theta + \phi}2 \right) }[/math]

Therefore,

[math]\displaystyle{ \sin \theta \pm \sin \phi = 2 \sin \left( \frac{\theta\pm \phi}2 \right) \cos \left( \frac{\theta\mp \phi}2 \right) }[/math]

Proof of cosine identities

Similarly for cosine, start with the sum-angle identities:

[math]\displaystyle{ \cos (\alpha + \beta) = \cos \alpha \cos \beta\ - \sin \alpha \sin \beta }[/math]

[math]\displaystyle{ \cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta }[/math]

Again, by adding and subtracting

[math]\displaystyle{ \cos (\alpha + \beta) + \cos (\alpha - \beta) = \cos \alpha \cos \beta\ - \sin \alpha \sin \beta + \cos \alpha \cos \beta + \sin \alpha \sin \beta = 2\cos \alpha \cos \beta }[/math]

[math]\displaystyle{ \cos (\alpha + \beta) - \cos (\alpha - \beta) = \cos \alpha \cos \beta\ - \sin \alpha \sin \beta - \cos \alpha \cos \beta - \sin \alpha \sin \beta = -2 \sin \alpha \sin \beta }[/math]

Substitute [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math] as before,

[math]\displaystyle{ \cos \theta + \cos \phi = 2 \cos \left( \frac{\theta+\phi}2 \right) \cos \left( \frac{\theta-\phi}2 \right) }[/math]

[math]\displaystyle{ \cos \theta - \cos \phi = -2 \sin \left( \frac{\theta+\phi}2 \right) \sin \left( \frac{\theta-\phi}2 \right) }[/math]

Inequalities

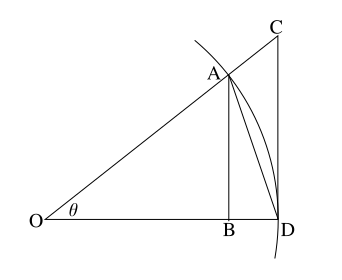
Illustration of the sine and tangent inequalities.

The figure at the right shows a sector of a circle with radius 1. The sector is $θ /(2 π)$ of the whole circle, so its area is $θ /2$ . We assume here that $θ < π /2$ .

[math]\displaystyle{ OA = OD = 1 }[/math]

[math]\displaystyle{ AB = \sin \theta }[/math]

[math]\displaystyle{ CD = \tan \theta }[/math]

The area of triangle $OAD$ is $AB /2$ , or $sin(θ)/2$ . The area of triangle $OCD$ is $CD /2$ , or $tan(θ)/2$ .

Since triangle $OAD$ lies completely inside the sector, which in turn lies completely inside triangle $OCD$ , we have

[math]\displaystyle{ \sin \theta \lt \theta \lt \tan \theta. }[/math]

This geometric argument relies on definitions of arc length and area, which act as assumptions, so it is rather a condition imposed in construction of trigonometric functions than a provable property.^[2] For the sine function, we can handle other values. If $θ > π /2$ , then $θ > 1$ . But $sin θ \leq 1$ (because of the Pythagorean identity), so $sin θ < θ$ . So we have

[math]\displaystyle{ \frac{\sin \theta}{\theta} \lt 1\ \ \ \mathrm{if}\ \ \ 0 \lt \theta. }[/math]

For negative values of $θ$ we have, by the symmetry of the sine function

[math]\displaystyle{ \frac{\sin \theta}{\theta} = \frac{\sin (-\theta)}{-\theta} \lt 1. }[/math]

Hence

[math]\displaystyle{ \frac{\sin \theta}{\theta} \lt 1\quad \text{if }\quad \theta \ne 0, }[/math]

and

[math]\displaystyle{ \frac{\tan \theta}{\theta} \gt 1\quad \text{if }\quad 0 \lt \theta \lt \frac{\pi}{2}. }[/math]

Identities involving calculus

Preliminaries

[math]\displaystyle{ \lim_{\theta \to 0}{\sin \theta} = 0 }[/math]

[math]\displaystyle{ \lim_{\theta \to 0}{\cos \theta} = 1 }[/math]

Sine and angle ratio identity

[math]\displaystyle{ \lim_{\theta \to 0}{\frac{\sin \theta}{\theta}} = 1 }[/math]

In other words, the function sine is differentiable at 0, and its derivative is 1.

Proof: From the previous inequalities, we have, for small angles

[math]\displaystyle{ \sin \theta \lt \theta \lt \tan \theta }[/math],

Therefore,

[math]\displaystyle{ \frac{\sin \theta}{\theta} \lt 1 \lt \frac{\tan \theta}{\theta} }[/math],

Consider the right-hand inequality. Since

[math]\displaystyle{ \tan \theta = \frac{\sin \theta}{\cos \theta} }[/math]

[math]\displaystyle{ \therefore 1 \lt \frac{\sin \theta}{\theta \cos \theta} }[/math]

Multiply through by [math]\displaystyle{ \cos \theta }[/math]

[math]\displaystyle{ \cos \theta \lt \frac{\sin \theta}{\theta} }[/math]

Combining with the left-hand inequality:

[math]\displaystyle{ \cos \theta \lt \frac{\sin \theta}{\theta} \lt 1 }[/math]

Taking [math]\displaystyle{ \cos \theta }[/math] to the limit as [math]\displaystyle{ \theta \to 0 }[/math]

[math]\displaystyle{ \lim_{\theta \to 0}{\cos \theta} = 1 }[/math]

Therefore,

[math]\displaystyle{ \lim_{\theta \to 0}{\frac{\sin \theta}{\theta}} = 1 }[/math]

Cosine and angle ratio identity

[math]\displaystyle{ \lim_{\theta \to 0}\frac{1 - \cos \theta}{\theta} = 0 }[/math]

Proof:

[math]\displaystyle{ \begin{align} \frac{1 - \cos \theta}{\theta} & = \frac{1 - \cos^2 \theta}{\theta (1 + \cos \theta)}\\ & = \frac{\sin^2 \theta}{\theta (1 + \cos \theta)}\\ & = \left( \frac{\sin \theta}{\theta} \right) \times \sin \theta \times \left( \frac{1}{1 + \cos \theta} \right)\\ \end{align} }[/math]

The limits of those three quantities are 1, 0, and 1/2, so the resultant limit is zero.

Cosine and square of angle ratio identity

[math]\displaystyle{ \lim_{\theta \to 0}\frac{1 - \cos \theta}{\theta^2} = \frac{1}{2} }[/math]

Proof:

As in the preceding proof,

[math]\displaystyle{ \frac{1 - \cos \theta}{\theta^2} = \frac{\sin \theta}{\theta} \times \frac{\sin \theta}{\theta} \times \frac{1}{1 + \cos \theta}. }[/math]

The limits of those three quantities are 1, 1, and 1/2, so the resultant limit is 1/2.

Proof of compositions of trig and inverse trig functions

All these functions follow from the Pythagorean trigonometric identity. We can prove for instance the function

[math]\displaystyle{ \sin[\arctan(x)]=\frac{x}{\sqrt{1+x^2}} }[/math]

Proof:

We start from

[math]\displaystyle{ \sin^2\theta+\cos^2\theta=1 }[/math] (I)

Then we divide this equation (I) by [math]\displaystyle{ \cos^2\theta }[/math]

[math]\displaystyle{ \cos^2\theta=\frac{1}{\tan^2\theta+1} }[/math] (II)

[math]\displaystyle{ 1-\sin^2\theta=\frac{1}{\tan^2\theta+1} }[/math]

Then use the substitution [math]\displaystyle{ \theta=\arctan(x) }[/math]:

[math]\displaystyle{ 1-\sin^2[\arctan(x)]=\frac{1}{\tan^2[\arctan(x)]+1} }[/math]

[math]\displaystyle{ \sin^2[\arctan(x)]=\frac{\tan^2[\arctan(x)]}{\tan^2[\arctan(x)]+1} }[/math]

Then we use the identity [math]\displaystyle{ \tan[\arctan(x)]\equiv x }[/math]

[math]\displaystyle{ \sin[\arctan(x)]=\frac{x}{\sqrt{x^2+1}} }[/math] (III)

And initial Pythagorean trigonometric identity proofed...

Similarly if we divide this equation (I) by [math]\displaystyle{ \sin^2\theta }[/math]

[math]\displaystyle{ \sin^2\theta=\frac{\frac{1}{1}}{1+\frac{1}{\tan^2\theta}} }[/math] (II)

[math]\displaystyle{ \sin^2\theta=\frac{\tan^2\theta}{\tan^2\theta+1} }[/math]

Then use the substitution [math]\displaystyle{ \theta=\arctan(x) }[/math]:

[math]\displaystyle{ \sin^2[\arctan(x)]=\frac{\tan^2[\arctan(x)]}{\tan^2[\arctan(x)]+1} }[/math]

Then we use the identity [math]\displaystyle{ \tan[\arctan(x)]\equiv x }[/math]

[math]\displaystyle{ \sin[\arctan(x)]=\frac{x}{\sqrt{x^2+1}} }[/math] (III)

And initial Pythagorean trigonometric identity proofed...

[math]\displaystyle{ [\arctan(x)]=[\arcsin(\frac{x}{\sqrt{x^2+1}})] }[/math]

[math]\displaystyle{ y=\frac{x}{\sqrt{x^2+1}} }[/math]

[math]\displaystyle{ y^2=\frac{x^2}{x^2+1} }[/math] (IV)

Let we guess that we have to prove:

[math]\displaystyle{ x=\frac{y}{\sqrt{1-y^2}} }[/math]

[math]\displaystyle{ x^2=\frac{y^2}{1-y^2} }[/math] (V)

Replacing (V) into (IV) :

[math]\displaystyle{ y^2=\frac{\frac{y^2}{(1-y^2)}}{\frac{y^2}{(1-y^2)}+1} }[/math]

[math]\displaystyle{ y^2=\frac{\frac{y^2}{(1-y^2)}}{\frac{1}{(1-y^2)}} }[/math]

So it's true: [math]\displaystyle{ y^2=y^2 }[/math] and guessing statement was true: [math]\displaystyle{ x=\frac{y}{\sqrt{1-y^2}} }[/math]

[math]\displaystyle{ [\arctan(x)]=[\arcsin(\frac{x}{\sqrt{x^2+1}})]=[\arcsin(y)]=[\arctan(\frac{y}{\sqrt{1-y^2}})] }[/math]

Now y can be written as x ; and we have [arcsin] expressed through [arctan]...

[math]\displaystyle{ [\arcsin(x)]=[\arctan(\frac{x}{\sqrt{1-x^2}})] }[/math]

Similarly if we seek :[math]\displaystyle{ [\arccos(x)] }[/math]...

[math]\displaystyle{ \cos[\arccos(x)]=x }[/math]

[math]\displaystyle{ \cos(\frac{\pi}{2}-(\frac{\pi}{2}-[\arccos(x)]))=x }[/math]

[math]\displaystyle{ \sin(\frac{\pi}{2}-[\arccos(x)])=x }[/math]

[math]\displaystyle{ \frac{\pi}{2}-[\arccos(x)]=[\arcsin(x)] }[/math]

[math]\displaystyle{ [\arccos(x)]=\frac{\pi}{2}-[\arcsin(x)] }[/math]

From :[math]\displaystyle{ [\arcsin(x)] }[/math]...

[math]\displaystyle{ [\arccos(x)]=\frac{\pi}{2}-[\arctan(\frac{x}{\sqrt{1-x^2}})] }[/math]

[math]\displaystyle{ [\arccos(x)]=\frac{\pi}{2}-[\arccot(\frac{\sqrt{1-x^2}}{x})] }[/math]

And finally we have [arccos] expressed through [arctan]...

[math]\displaystyle{ [\arccos(x)]=[\arctan(\frac{\sqrt{1-x^2}}{x})] }[/math]

Notes

↑ "Tangent Identity | Math 老师". Archived from the original on 2013-10-29. https://web.archive.org/web/20131029203121/http://mathlaoshi.com/tags/tangent-identity/. Retrieved 2013-10-30. dead link
↑ Richman, Fred (March 1993). "A Circular Argument". The College Mathematics Journal 24 (2): 160–162. doi:10.2307/2686787.

References

E. T. Whittaker and G. N. Watson. A Course of Modern Analysis, Cambridge University Press , 1952

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Proofs of trigonometric identities. Read more

[1] "Tangent Identity | Math 老师". Archived from the original on 2013-10-29. https://web.archive.org/web/20131029203121/http://mathlaoshi.com/tags/tangent-identity/. Retrieved 2013-10-30. dead link

[2] Richman, Fred (March 1993). "A Circular Argument". The College Mathematics Journal 24 (2): 160–162. doi:10.2307/2686787.

[1]

[2]

Anonymous

Search

Proofs of trigonometric identities

Namespaces

More

Page actions

Contents

Elementary trigonometric identities

Definitions

Ratio identities

Complementary angle identities

Pythagorean identities

Angle sum identities

Sine

Cosine

Tangent and cotangent

Double-angle identities

Half-angle identities

Miscellaneous – the triple tangent identity

Miscellaneous – the triple cotangent identity

Sum to product identities

Proof of sine identities

Proof of cosine identities

Inequalities

Identities involving calculus

Preliminaries

Sine and angle ratio identity

Cosine and angle ratio identity

Cosine and square of angle ratio identity

Proof of compositions of trig and inverse trig functions

See also

Notes

References

Navigation

Navigation

Help

Translate

Wiki tools

Wiki tools

Anonymous

Search

Proofs of trigonometric identities

Elementary trigonometric identities

Definitions

Ratio identities

Complementary angle identities

Pythagorean identities

Angle sum identities

Sine

Cosine

Tangent and cotangent

Double-angle identities

Half-angle identities

Miscellaneous – the triple tangent identity

Miscellaneous – the triple cotangent identity

Sum to product identities

Proof of sine identities

Proof of cosine identities

Inequalities

Identities involving calculus

Preliminaries

Sine and angle ratio identity

Cosine and angle ratio identity

Cosine and square of angle ratio identity

Proof of compositions of trig and inverse trig functions

See also

Notes

References

Navigation

Wiki tools

Page tools

Other projects

Categories