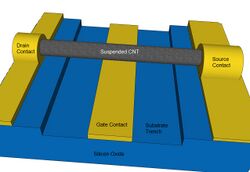
Chemistry:Carbon nanotube field-effect transistor

From HandWiki
Revision as of 06:55, 8 February 2024 by LinuxGuru (talk | contribs) (fixing)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Field-effect transistor made from carbon nsnotubes

A carbon nanotube field-effect transistor (CNTFET) is a field-effect transistor that utilizes a single carbon nanotube (CNT) or an array of carbon nanotubes as the channel material, instead of bulk silicon, as in the traditional MOSFET structure. There have been major developments since CNTFETs were first demonstrated in 1998.[1][2]

Background

A diagram showing that a carbon nanotube is essentially rolled up graphene

According to Moore's law, the dimensions of individual devices in an integrated circuit have been decreased by a factor of approximately two every two years. This scaling down of devices has been the driving force in technological advances since the late 20th century. However, as noted by ITRS 2009 edition, further scaling down has faced serious limits related to fabrication technology and device performances as the critical dimension shrunk down to sub-22 nm range.[3] The limits involve electron tunneling through short channels and thin insulator films, the associated leakage currents, passive power dissipation, short channel effects, and variations in device structure and doping.[4] These limits can be overcome to some extent and facilitate further scaling down of device dimensions by modifying the channel material in the traditional bulk MOSFET structure with a single carbon nanotube or an array of carbon nanotubes.

A carbon nanotube’s bandgap is directly affected by its chiral angle and diameter. If those properties can be controlled, CNTs would be a promising candidate for future nano-scale transistor devices. Moreover, because of the lack of boundaries in the perfect and hollow cylinder structure of CNTs, there is no boundary scattering. CNTs are also quasi-1D materials in which only forward scattering and back scattering are allowed, and elastic scattering means that free paths in carbon nanotubes are long, typically on the order of micrometers. As a result, quasi-ballistic transport can be observed in nanotubes at relatively long lengths and low fields.[5] Because of the strong covalent carbon–carbon bonding in the sp2 configuration, carbon nanotubes are chemically inert and are able to transport large electric currents. In theory, carbon nanotubes are also able to conduct heat nearly as well as diamond or sapphire, and because of their miniaturized dimensions, the CNTFET should switch reliably using much less power than a silicon-based device.[6]

Electronic structure of carbon nanotubes

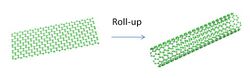
Graphene atomic structure with a translational vector T and a chiral vector Ĉh of a CNT
One-dimensional energy dispersion relations for (a) (n,m)=(5,5) metallic tube, (b) (n,m)=(10,0) semiconducting tube.

To a first approximation, the exceptional electrical properties of carbon nanotubes can be viewed as inherited from the unique electronic structure of graphene, provided the carbon nanotube is thought of as graphene rolled up along one of its Bravais lattice vectors Ĉh to form a hollow cylinder.[7] [8] [9] In this construction, periodic boundary conditions are imposed over Ĉh to yield a lattice of seamlessly bonded carbon atoms on the cylinder surface.[10]

Thus, the circumference of such a carbon nanotube can be expressed in terms of its rollup vector: Ĉh=nâ1+mâ2 that connects two crystallographically equivalent sites of the two-dimensional graphene sheet. Here [math]\displaystyle{ n }[/math] and [math]\displaystyle{ m }[/math] are integers and â1 and â2 are primitive lattice vectors of the hexagonal lattice. Therefore, the structure of any carbon nanotube can be described by an index with a pair of integers [math]\displaystyle{ (n,m) }[/math] that define its rollup vector.[8] In terms of the integers [math]\displaystyle{ (n,m) }[/math], the nanotube diameter [math]\displaystyle{ d_t }[/math] and the chiral angle [math]\displaystyle{ \theta }[/math] are given by: [math]\displaystyle{ d_t=(\sqrt{3}\,d_0/\pi)\sqrt{m^2+mn+n^2} }[/math]; and, [math]\displaystyle{ \theta = \tan^{-1}[\sqrt3\,n/(2m+n)] }[/math], where [math]\displaystyle{ d_0 }[/math] is the C—C bond distance.

Differences in the chiral angle and the diameter cause the differences in the properties of the various carbon nanotubes. For example, it can be shown that an [math]\displaystyle{ (n,m) }[/math] carbon nanotube is metallic when [math]\displaystyle{ n=m }[/math],[7] is a small band gap semiconductor when [math]\displaystyle{ n-m= 3i }[/math] and [math]\displaystyle{ i\ne 0 }[/math],[8] [9] and is a moderate band gap semiconductor when [math]\displaystyle{ n-m\ne 3i }[/math],[8] [9] where [math]\displaystyle{ i }[/math] is an integer.

These results can be motivated by noting that periodic boundary conditions for 1D carbon nanotubes permit only a few wave vectors to exist around their circumferences. Metallic conduction could be expected to occur when one of these wave vectors passes through the K-point of graphene’s 2D hexagonal Brillouin zone, where the valence and conduction bands are degenerate.

This analysis, however, neglects the effects of curvature caused by rolling up the graphene sheet that converts all nanotubes with [math]\displaystyle{ n-m=3i }[/math] to small band gap semiconductors,[8] [9] with the exception of the armchair tubes ([math]\displaystyle{ n=m }[/math]) that remain metallic.[7] Although the band gaps of carbon nanotubes with [math]\displaystyle{ n-m= 3i }[/math] and [math]\displaystyle{ i\ne 0 }[/math] are relatively small, some can still easily exceed room temperature, if the nanotube diameter is about a nanometer.[11] [12]

The band gaps [math]\displaystyle{ E_g }[/math] of semiconducting carbon nanotubes with [math]\displaystyle{ n-m\ne 3i }[/math] depend predominately on their diameters. In fact, according to a single-particle tight-binding description of the electronic structure of these nanotubes [math]\displaystyle{ E_g=2|V_0|(d_0/d_t), }[/math][13] where [math]\displaystyle{ V_0 }[/math] is the nearest-neighbor hopping matrix element. That this result is an excellent approximation so long as [math]\displaystyle{ (d_0/d_t) }[/math] is a lot less than one has been verified both by all-electron first principles local density functional calculations[14] and experiment.[15]

Scatter plots of the band gaps of carbon nanotubes with diameters up to three nanometers calculated using an all valence tight binding model that includes curvature effects appeared early in carbon nanotube research[11] and were reprinted in a review.[16]

Device fabrication

There are many types of CNTFET devices; a general survey of the most common geometries are covered below.

Back-gated CNTFETs

Top view
Top view
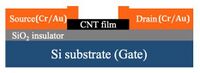
Side view
Side view
Top and side view of a silicon back-gated CNTFET. The CNTFET consists of carbon nanotubes deposited on a silicon oxide substrate pre-patterned with chromium/gold source and drain contacts.

The earliest techniques for fabricating carbon nanotube (CNT) field-effect transistors involved pre-patterning parallel strips of metal across a silicon dioxide substrate, and then depositing the CNTs on top in a random pattern.[1][2] The semiconducting CNTs that happened to fall across two metal strips meet all the requirements necessary for a rudimentary field-effect transistor. One metal strip is the "source" contact while the other is the "drain" contact. The silicon oxide substrate can be used as the gate oxide and adding a metal contact on the back makes the semiconducting CNT gateable.

This technique suffered from several drawbacks, which made for non-optimized transistors. The first was the metal contact, which actually had very little contact to the CNT, since the nanotube just lay on top of it and the contact area was therefore very small. Also, due to the semiconducting nature of the CNT, a Schottky barrier forms at the metal–semiconductor interface,[17] increasing the contact resistance. The second drawback was due to the back-gate device geometry. Its thickness made it difficult to switch the devices on and off using low voltages, and the fabrication process led to poor contact between the gate dielectric and CNT.[18]

Top-gated CNTFETs

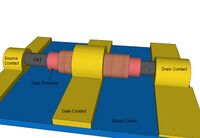
The process for fabricating a top-gated CNTFET.

Eventually, researchers migrated from the back-gate approach to a more advanced top-gate fabrication process.[18] In the first step, single-walled carbon nanotubes are solution deposited onto a silicon oxide substrate. Individual nanotubes are then located via atomic force microscope or scanning electron microscope. After an individual tube is isolated, source and drain contacts are defined and patterned using high resolution electron beam lithography. A high temperature anneal step reduces the contact resistance by improving adhesion between the contacts and CNT.[19] A thin top-gate dielectric is then deposited on top of the nanotube, either via evaporation or atomic layer deposition. Finally, the top gate contact is deposited on the gate dielectric, completing the process.

Arrays of top-gated CNTFETs can be fabricated on the same wafer, since the gate contacts are electrically isolated from each other, unlike in the back-gated case. Also, due to the thinness of the gate dielectric, a larger electric field can be generated with respect to the nanotube using a lower gate voltage. These advantages mean top-gated devices are generally preferred over back-gated CNTFETs, despite their more complex fabrication process.

Wrap-around gate CNTFETs

Sheathed CNT
Gate all-around CNT Device

Wrap-around gate CNTFETs, also known as gate-all-around CNTFETs were developed in 2008,[20] and are a further improvement upon the top-gate device geometry. In this device, instead of gating just the part of the CNT that is closer to the metal gate contact, the entire circumference of the nanotube is gated. This should ideally improve the electrical performance of the CNTFET, reducing leakage current and improving the device on/off ratio.

Device fabrication begins by first wrapping CNTs in a gate dielectric and gate contact via atomic layer deposition.[21] These wrapped nanotubes are then solution-deposited on an insulating substrate, where the wrappings are partially etched off, exposing the ends of the nanotube. The source, drain, and gate contacts are then deposited onto the CNT ends and the metallic outer gate wrapping.

Suspended CNTFETs

A suspended CNTFET device.

Yet another CNTFET device geometry involves suspending the nanotube over a trench to reduce contact with the substrate and gate oxide.[22] This technique has the advantage of reduced scattering at the CNT-substrate interface, improving device performance.[22][23][24] There are many methods used to fabricate suspended CNTFETs, ranging from growing them over trenches using catalyst particles,[22] transferring them onto a substrate and then under-etching the dielectric beneath,[24] and transfer-printing onto a trenched substrate.[23]

The main problem suffered by suspended CNTFETs is that they have very limited material options for use as a gate dielectric (generally air or vacuum), and applying a gate bias has the effect of pulling the nanotube closer to the gate, which places an upper limit on how much the nanotube can be gated. This technique will also only work for shorter nanotubes, as longer tubes will flex in the middle and droop towards the gate, possibly touching the metal contact and shorting the device. In general, suspended CNTFETs are not practical for commercial applications, but they can be useful for studying the intrinsic properties of clean nanotubes.

CNTFET material considerations

There are general decisions one must make when considering what materials to use when fabricating a CNTFET. Semiconducting single-walled carbon nanotubes are preferred over metallic single-walled and metallic multi-walled tubes since they are able to be fully switched off, at least for low source/drain biases. A lot of work has been put into finding a suitable contact material for semiconducting CNTs; the best material to date is Palladium, because its work function closely matches that of nanotubes and it adheres to the CNTs quite well.[25]

Characteristics

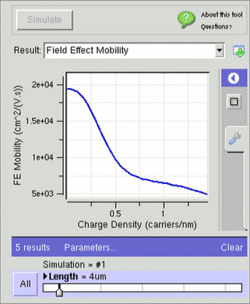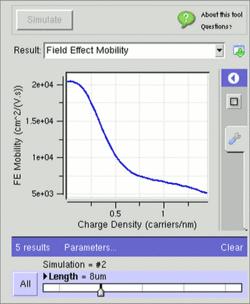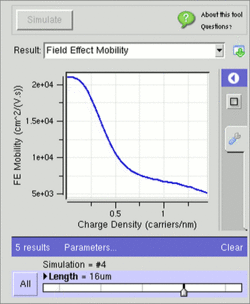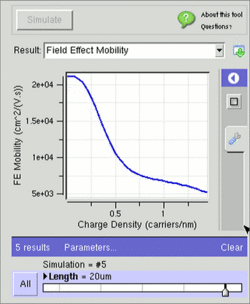
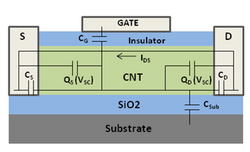
Field effect mobility of a back-gated CNTFET device with varying channel lengths. SiO2 is used as the gate dielectric. Tool: 'CNT Mobility' at nanoHUB.org[26][unreliable source?]

In CNT–metal contacts, the different work functions of the metal and the CNT result in a Schottky barrier at the source and drain, which are made of metals like silver, titanium, palladium and aluminum.[27] Even though like Schottky barrier diodes, the barriers would have made this FET to transport only one type of carrier, the carrier transport through the metal-CNT interface is dominated by quantum mechanical tunneling through the Schottky barrier. CNTFETs can easily be thinned by the gate field such that tunneling through them results in a substantial current contribution. CNTFETs are ambipolar; either electrons or holes, or both electrons and holes can be injected simultaneously.[27] This makes the thickness of the Schottky barrier a critical factor.

CNTFETs conduct electrons when a positive bias is applied to the gate and holes when a negative bias is applied, and drain current increases with increasing a magnitude of an applied gate voltage.[28] Around Vg = Vds/2, the current gets the minimum due to the same amount of the electron and hole contributions to the current.

Like other FETs, the drain current increases with an increasing drain bias unless the applied gate voltage is below the threshold voltage. For planar CNTFETs with different design parameters, the FET with a shorter channel length produces a higher saturation current, and the saturation drain current also becomes higher for the FET consisting of smaller diameter keeping the length constant. For cylindrical CNTFETs, it is clear that a higher drain current is driven than that of planar CNTFETs since a CNT is surrounded by an oxide layer which is finally surrounded by a metal contact serving as the gate terminal.[29]

Theoretical derivation of drain current

Structure of a top-gate CNT transistor

Theoretical investigation on drain current of the top-gate CNT transistor has been done by Kazierski and colleagues.[30] When an electric field is applied to a CNT transistor, a mobile charge is induced in the tube from the source and drain. These charges are from the density of positive velocity states filled by the source NS and that of negative velocity states filled by the drain ND,[30] and these densities are determined by the Fermi–Dirac probability distributions.

[math]\displaystyle{ N_S = \frac{1}{2}\int_{-\infty}^{+\infty} D(E)f(E-U_{SF})\,dE }[/math]
[math]\displaystyle{ N_D = \frac{1}{2}\int_{-\infty}^{+\infty} D(E)f(E-U_{DF})\,dE }[/math]

and the equilibrium electron density is

[math]\displaystyle{ N_0 = \frac{1}{2}\int_{-\infty}^{+\infty} D(E)f(E-E_{F})\,dE }[/math].

where the density of states at the channel D(E), USF, and UDF are defined as

[math]\displaystyle{ D(E) = D_0\frac{E}{\sqrt{E^2-(E_g/2)^2}}\Theta(E-E_g/2) }[/math]
[math]\displaystyle{ U_{SF} = E_F-qV_{SC} }[/math]
[math]\displaystyle{ U_{DF} = E_F-qV_{SC}-qV_{DS}. }[/math]

The term, [math]\displaystyle{ \Theta(E-E_g/2) }[/math] is 1 when the value inside the bracket is positive and 0 when negative. VSC is the self-consistent voltage that illustrates that the CNT energy is affected by external terminal voltages and is implicitly related to the device terminal voltages and charges at terminal capacitances by the following nonlinear equation:

[math]\displaystyle{ V_{SC} = \frac{-Q_t+qN_S(V_{SC})+qN_D(V_{SC})-qN_0}{C_\Sigma} }[/math]

where Qt represents the charge stored in terminal capacitances, and the total terminal capacitance CΣ is the sum of the gate, drain, source, and substrate capacitances shown in the figure above. The standard approach to the solution to the self-consistent voltage equation is to use the Newton–Raphson iterative method. According to the CNT ballistic transport theory, the drain current caused by the transport of the nonequilibrium charge across the nanotube can be calculated using the Fermi–Dirac statistics.

[math]\displaystyle{ I_{DS} = \frac{2qkT}{\pi{\hbar}}\left[ F_0 \left( \frac{U_{SF}}{kT} \right) - F_0 \left(\frac{U_{DF}}{kT}\right)\right] }[/math]

Here F0 represents the Fermi–Dirac integral of order 0, k is the Boltzmann constant, T is the temperature, and ℏ the reduced Planck constant. This equation can be solved easily as long as the self-consistent voltage is known. However the calculation could be time-consuming when it needs to solve the self-consistent voltage with the iterative method, and this is the main drawback of this calculation.

Heat dissipation

The decrease of the current and burning of the CNT can occur due to the temperature raised by several hundreds of kelvins. Generally, the self-heating effect is much less severe in a semiconducting CNTFET than in a metallic one due to different heat dissipation mechanisms. A small fraction of the heat generated in the CNTFET is dissipated through the channel. The heat is non-uniformly distributed, and the highest values appear at the source and drain sides of the channel.[31] Therefore, the temperature significantly gets lowered near the source and drain regions. For semiconducting CNT, the temperature rise has a relatively small effect on the I–V characteristics compared to silicon.

Comparison to MOSFETs

CNTFETs show different characteristics compared to MOSFETs in their performances. In a planar gate structure, the p-CNTFET produces ~1500 A/m of the on-current per unit width at a gate overdrive of 0.6 V while p-MOSFET produces ~500 A/m at the same gate voltage.[32] This on-current advantage comes from the high gate capacitance and improved channel transport. Since an effective gate capacitance per unit width of CNTFET is about double that of p-MOSFET, the compatibility with high-k gate dielectrics becomes a definite advantage for CNTFETs.[29] About twice higher carrier velocity of CNTFETs than MOSFETs comes from the increased mobility and the band structure. CNTFETs, in addition, have about four times higher transconductance.[citation needed]

The first sub-10-nanometer CNT transistor was made which outperformed the best competing silicon devices with more than four times the diameter-normalized current density (2.41 mA/μm) at an operating voltage of 0.5 V. The inverse subthreshold slope of the CNTFET was 94 mV/decade.[33]

Advantages

Disadvantages

Lifetime (degradation)

Carbon nanotubes have recently been shown to be stable in air for many months and likely more, even when under continual operation.[34] While gate voltages are being applied, the device current can experience some undesirable drift/settling, but changes in gating quickly reset this behavior with little change in threshold voltage.[34]

Reliability

Carbon nanotubes have shown reliability issues when operated under high electric field or temperature gradients. Avalanche breakdown occurs in semiconducting CNT and joule breakdown in metallic CNT. Unlike avalanche behavior in silicon, avalanche in CNTs is negligibly temperature-dependent. Applying high voltages beyond avalanche point results in Joule heating and eventual breakdown in CNTs.[35] This reliability issue has been studied, and it is noticed that the multi-channeled structure can improve the reliability of the CNTFET. The multi-channeled CNTFETs can keep a stable performance after several months, while the single-channeled CNTFETs usually wear out after a few weeks in the ambient atmosphere.[36] The multi-channeled CNTFETs keep operating when some channels break down, with a small change in electrical properties.

Difficulties in mass production, production cost

Although CNTs have unique properties such as stiffness, strength, and tenacity compared to other materials especially to silicon, there is currently no technology for their mass production, causing a high production cost. To overcome the fabrication difficulties, several methods have been studied such as direct growth, solution dropping, and various transfer printing techniques.[37] The most promising methods for mass production involve some degree of self-assembly of pre-produced nanotubes into the desired positions. Individually manipulating many tubes is impractical at a large scale and growing them in their final positions presents many challenges.

Future work

The most desirable future work involved in CNTFETs will be the transistor with higher reliability, cheap production cost, or the one with more enhanced performances. For example: adding effects external to the inner CNT transistor like the Schottky barrier between the CNT and metal contacts, multiple CNTs at a single gate,[30] channel fringe capacitances, parasitic source/drain resistance, and series resistance due to the scattering effects.

References

  1. ↑ 1.0 1.1 Dekker, Cees; Tans, Sander J.; Verschueren, Alwin R. M. (1998). "Room-temperature transistor based on a single carbon nanotube". Nature 393 (6680): 49–52. doi:10.1038/29954. Bibcode: 1998Natur.393...49T. 
  2. ↑ 2.0 2.1 Martel, R.; Schmidt, T.; Shea, H. R.; Hertel, T.; Avouris, Ph. (1998). "Single- and multi-wall carbon nanotube field-effect transistors". Applied Physics Letters 73 (17): 2447. doi:10.1063/1.122477. Bibcode: 1998ApPhL..73.2447M. http://www.dmphotonics.com/Trestles%20CW%20TiSapphire%20laser%20illuminates%20carbon%20nanotube%20field%20effect%20transistors/Single-%20and%20multi-wall%20carbon%20nanotube%20field-effect%20transistors_Martel_APL.pdf. 
  3. ↑ International Technology Roadmap for Semiconductors 2009 Edition
  4. ↑ Avouris, P; Chen, J (2006). "Nanotube electronics and optoelectronics". Materials Today 9 (10): 46–54. doi:10.1016/S1369-7021(06)71653-4. 
  5. ↑ H. Dai, A. Javey, E. Pop, D. Mann, Y. Lu, "Electrical Properties and Field-Effect Transistors of Carbon Nanotubes," Nano: Brief Reports and Reviews 1, 1 (2006).
  6. ↑ Collins, P.G.; Avouris, P. (2000). "Nanotubes for Electronics". Scientific American 283 (6): 62–69. doi:10.1038/scientificamerican1200-62. PMID 11103460. Bibcode: 2000SciAm.283f..62C. 
  7. ↑ 7.0 7.1 7.2 Mintmire, J.W.; Dunlap, B.I.; White, C.T. (3 February 1992). "Are fullerene tubules metallic?". Phys. Rev. Lett. 68 (5): 631–634. doi:10.1103/PhysRevLett.68.631. PMID 10045950. Bibcode: 1992PhRvL..68..631M. 
  8. ↑ 8.0 8.1 8.2 8.3 8.4 Hamada, N.; Sawada, S.; Oshiyama, A. (9 March 1992). "New one-dimensional conductors: graphitic microtubules". Phys. Rev. Lett. 68 (10): 1579–1581. doi:10.1103/PhysRevLett.68.1579. PMID 10045167. Bibcode: 1992PhRvL..68.1579H. 
  9. ↑ 9.0 9.1 9.2 9.3 Dresselhaus, M.; Dresselhaus, G.; Saito, Riichiro (15 July 1992). "Carbon fibers based on C60 and their symmetry". Physical Review B 45 (11): 6234–6242. doi:10.1103/PhysRevB.45.6234. PMID 10000369. Bibcode: 1992PhRvB..45.6234D. http://flex.phys.tohoku.ac.jp/~rsaito/rsj/p458.pdf. 
  10. ↑ Iijima, Sumio (7 November 1991). "Helical microtubules of graphitic carbon". Nature 354 (6348): 56–58. doi:10.1038/354056a0. Bibcode: 1991Natur.354...56I. 
  11. ↑ 11.0 11.1 White, C. T. et al. (April 1993). "Chapter 6: Predicting Properties of Fullerenes and their Derivatives". in Billups, W . E.; Ciufolini, M. A.. Buckminsterfullerenes. VCH Publishers, Inc., New York, New York. pp. 167. ISBN 1-56081-608-2. https://books.google.com/books?id=KoLEnvt0ej4C&q=Buckminsterfullerenes%2F&pg=PA125. 
  12. ↑ Ouyang, M; Huang, J. L.; Chung, C. L.; Lieber, C. M. (2001). "Energy Gaps in "metallic" single-walled carbon nanotubes". Science 292 (5517): 702–705. doi:10.1126/science.1058853. PMID 11326093. Bibcode: 2001Sci...292..702O. http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1019&context=chemistrycheung. 
  13. ↑ White, C.T.; Robertson,D.H; Mintmire, J.W (1993). "Helical and rotational symmetries of nanoscale graphitic tubules". Phys. Rev. B 68 (9): 5485–5488. doi:10.1103/PhysRevB.47.5485. PMID 10006726. Bibcode: 1993PhRvB..47.5485W. 
  14. ↑ Mintmire, J.W.; White, C.T. (1995). "Electronic and structural properties of carbon nanotubes". Carbon 33 (7): 891–902. doi:10.1016/0008-6223(95)00018-9. 
  15. ↑ Wildoer J.W.G.; Venema, L.C.; Rinzler, A.G.; Smalley, R.E.; Dekker, C. (1998). "Electronic structure of atomically resolved carbon nanotubes". Nature 391 (6662): 58–62. doi:10.1038/34139. Bibcode: 1998Natur.391...59W. 
  16. ↑ White, C.T.; Mintmire, J.W (2005). "Fundamental properties of single-wall carbon nanotubes". J. Phys. Chem. B 109 (1): 52–65. doi:10.1021/jp047416. PMID 16850984. 
  17. ↑ Heinze, S; Tersoff, J; Martel, R; Derycke, V; Appenzeller, J; Avouris, P (2002). "Carbon nanotubes as Schottky barrier transistors". Physical Review Letters 89 (10): 106801. doi:10.1103/PhysRevLett.89.106801. PMID 12225214. Bibcode: 2002PhRvL..89j6801H. http://researchweb.watson.ibm.com/nanoscience/Heinze_Schottky.pdf. 
  18. ↑ 18.0 18.1 Wind, S. J.; Appenzeller, J.; Martel, R.; Derycke, V.; Avouris, Ph. (2002). "Vertical scaling of carbon nanotube field-effect transistors using top gate electrodes". Applied Physics Letters 80 (20): 3817. doi:10.1063/1.1480877. Bibcode: 2002ApPhL..80.3817W. http://140.120.11.121/~lcli/file/periodical/Carbon/Snowapl2004/ref4windapl2002.pdf. 
  19. ↑ Lim, Seong Chu (November 2006). "A strategy for forming robust adhesion with the substrate in a carbon-nanotube field-emission array". Carbon 44 (13): 2809. doi:10.1016/j.carbon.2006.03.030. 
  20. ↑ Chen, Zhihong; Farmer, Damon; Xu, Sheng; Gordon, Roy; Avouris, Phaedon; Appenzeller, Joerg (2008). "Externally Assembled Gate-All-Around Carbon Nanotube Field-Effect Transistor". IEEE Electron Device Letters 29 (2): 183–185. doi:10.1109/LED.2007.914069. Bibcode: 2008IEDL...29..183C. https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=1173&context=nanodocs. 
  21. ↑ Farmer, DB; Gordon, RG (2006). "Atomic layer deposition on suspended single-walled carbon nanotubes via gas-phase noncovalent functionalization". Nano Letters 6 (4): 699–703. doi:10.1021/nl052453d. PMID 16608267. Bibcode: 2006NanoL...6..699F. 
  22. ↑ 22.0 22.1 22.2 Cao, J; Wang, Q; Dai, H (2005). "Electron transport in very clean, as-grown suspended carbon nanotubes". Nature Materials 4 (10): 745–9. doi:10.1038/nmat1478. PMID 16142240. Bibcode: 2005NatMa...4..745C. 
  23. ↑ 23.0 23.1 Sangwan, V. K.; Ballarotto, V. W.; Fuhrer, M. S.; Williams, E. D. (2008). "Facile fabrication of suspended as-grown carbon nanotube devices". Applied Physics Letters 93 (11): 113112. doi:10.1063/1.2987457. Bibcode: 2008ApPhL..93k3112S. 
  24. ↑ 24.0 24.1 Lin, Yu-Ming; Tsang, James C; Freitag, Marcus; Avouris, Phaedon (2007). "Impact of oxide substrate on electrical and optical properties of carbon nanotube devices". Nanotechnology 18 (29): 295202. doi:10.1088/0957-4484/18/29/295202. Bibcode: 2007Nanot..18C5202L. http://gr-sci.net/papers/suspended_nanotube_Nanotechnology2007.pdf. 
  25. ↑ Javey, Ali; Guo, Jing; Wang, Qian; Lundstrom, Mark; Dai, Hongjie (2003). "Ballistic carbon nanotube field-effect transistors". Nature 424 (6949): 654–7. doi:10.1038/nature01797. PMID 12904787. Bibcode: 2003Natur.424..654J. http://www.stanford.edu/dept/chemistry/faculty/dai/group/Reprint/63.pdf. 
  26. ↑ Zhao, Y. (2014). CNT Mobility. doi:10.4231/D3V698C9Z. 
  27. ↑ 27.0 27.1 Avouris, Phaedon; Chen, Zhihong; Perebeinos, Vasili (2007). "Carbon-based electronics". Nature Nanotechnology 2 (10): 605–15. doi:10.1038/nnano.2007.300. PMID 18654384. Bibcode: 2007NatNa...2..605A. 
  28. ↑ P.Avouris et al, "Electronics and Optoelectronics with Carbon Nanotubes," American Institute of Physics, 18–21, June/July 2004. (pdf version )
  29. ↑ 29.0 29.1 S.Rasmita et al, "Simulation of Carbon Nanotube Field Effect Transistors," International Journal of Electronic Engineering Research, 117–125 Vol.1, No.2 (2009)
  30. ↑ 30.0 30.1 30.2 Kazmierski, Tom J.; Zhou, Dafeng; Al-Hashimi, Bashir M.; Ashburn, Peter (2010). "Numerically Efficient Modeling of CNT Transistors with Ballistic and Nonballistic Effects for Circuit Simulation". IEEE Transactions on Nanotechnology 9 (1): 99–107. doi:10.1109/TNANO.2009.2017019. Bibcode: 2010ITNan...9...99K. https://eprints.soton.ac.uk/267152/1/nano090302.pdf. 
  31. ↑ Ouyang, Yijian; Guo, Jing (2006). "Heat dissipation in carbon nanotube transistors". Applied Physics Letters 89 (18): 183122. doi:10.1063/1.2382734. Bibcode: 2006ApPhL..89r3122O. 
  32. ↑ Jing Guo; Datta, S.; Lundstrom, M.; Brink, M.; McEuen, P.; Javey, A.; Hongjie Dai; Hyoungsub Kim et al. (2002). "Assessment of silicon MOS and carbon nanotube FET performance limits using a general theory of ballistic transistors". p. 711. doi:10.1109/IEDM.2002.1175937. ISBN 0-7803-7462-2. http://www.guo.ece.ufl.edu/iedm02_final.pdf. 
  33. ↑ Franklin, Aaron D.; Luisier, Mathieu; Han, Shu-Jen; Tulevski, George; Breslin, Chris M.; Gignac, Lynne; Lundstrom, Mark S.; Haensch, Wilfried (2012-02-08). "Sub-10 nm Carbon Nanotube Transistor". Nano Letters 12 (2): 758–762. doi:10.1021/nl203701g. ISSN 1530-6984. PMID 22260387. Bibcode: 2012NanoL..12..758F. 
  34. ↑ 34.0 34.1 Noyce, Steven G.; Doherty, James L.; Cheng, Zhihui; Han, Hui; Bowen, Shane; Franklin, Aaron D. (2019-02-05). "Electronic Stability of Carbon Nanotube Transistors Under Long-Term Bias Stress". Nano Letters (American Chemical Society (ACS)) 19 (3): 1460–1466. doi:10.1021/acs.nanolett.8b03986. ISSN 1530-6984. PMID 30720283. Bibcode: 2019NanoL..19.1460N. 
  35. ↑ Pop, Eric; Dutta, Sumit; Estrada, David; Liao, Albert (2009). "Avalanche, joule breakdown and hysteresis in carbon nanotube transistors". p. 405. doi:10.1109/IRPS.2009.5173287. ISBN 978-1-4244-2888-5. http://poplab.ece.illinois.edu/pdfs/Pop_CNTreliability_IRPS09.pdf. 
  36. ↑ C.Changxin and Z.Yafei, "Nanowelded Carbon Nanotubes: From Field-Effect Transistor to Solar Microcells" Nano Science and Technology series (2009), pp. 63 ff ISBN:3-642-01498-4
  37. ↑ Chang-Jian, Shiang-Kuo; Ho, Jeng-Rong; John Cheng, J.-W. (2010). "Characterization of developing source/drain current of carbon nanotube field-effect transistors with n-doping by polyethylene imine". Microelectronic Engineering 87 (10): 1973–1977. doi:10.1016/j.mee.2009.12.019. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Chemistry:Carbon_nanotube_field-effect_transistor&oldid=3420732"