Quantum error correction

Short description: Process in quantum computing

Quantum error correction (QEC) is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is theorised as essential to achieve fault tolerant quantum computing that can reduce the effects of noise on stored quantum information, faulty quantum gates, faulty quantum preparation, and faulty measurements. This would allow algorithms of greater circuit depth.

Classical error correction employs redundancy. The simplest albeit inefficient approach is the repetition code. The idea is to store the information multiple times, and—if these copies are later found to disagree—take a majority vote; e.g. suppose we copy a bit in the one state three times. Suppose further that a noisy error corrupts the three-bit state so that one of the copied bits is equal to zero but the other two are equal to one. Assuming that noisy errors are independent and occur with some sufficiently low probability p, it is most likely that the error is a single-bit error and the transmitted message is three ones. It is possible that a double-bit error occurs and the transmitted message is equal to three zeros, but this outcome is less likely than the above outcome. In this example, the logical information was a single bit in the one state, the physical information are the three copied bits, and determining what logical state is encoded in the physical state is called decoding. Similar to classical error correction, QEC codes do not always correctly decode logical qubits, but their use reduces the effect of noise.

Copying quantum information is not possible due to the no-cloning theorem. This theorem seems to present an obstacle to formulating a theory of quantum error correction. But it is possible to spread the (logical) information of one qubit onto a highly entangled state of several (physical) qubits. Peter Shor first discovered this method of formulating a quantum error correcting code by storing the information of one qubit onto a highly entangled state of nine qubits.

Classical error correcting codes use a syndrome measurement to diagnose which error corrupts an encoded state. An error can then be reversed by applying a corrective operation based on the syndrome. Quantum error correction also employs syndrome measurements. It performs a multi-qubit measurement that does not disturb the quantum information in the encoded state but retrieves information about the error. Depending on the QEC code used, syndrome measurement can determine the occurrence, location and type of errors. In most QEC codes, the type of error is either a bit flip, or a sign (of the phase) flip, or both (corresponding to the Pauli matrices X, Z, and Y). The measurement of the syndrome has the projective effect of a quantum measurement, so even if the error due to the noise was arbitrary, it can be expressed as a combination of basis operations called the error basis (which is given by the Pauli matrices and the identity). To correct the error, the Pauli operator corresponding to the type of error is used on the corrupted qubit to revert the effect of the error.

The syndrome measurement provides information about the error that has happened, but not about the information that is stored in the logical qubit—as otherwise the measurement would destroy any quantum superposition of this logical qubit with other qubits in the quantum computer, which would prevent it from being used to convey quantum information.

Bit flip code

The repetition code works in a classical channel, because classical bits are easy to measure and to repeat. This approach does not work for a quantum channel in which, due to the no-cloning theorem, it is not possible to repeat a single qubit three times. To overcome this, a different method has to be used, such as the three-qubit bit flip code first proposed by Asher Peres in 1985. This technique uses entanglement and syndrome measurements and is comparable in performance with the repetition code.

Quantum circuit of the bit flip code

Consider the situation in which we want to transmit the state of a single qubit [math]\displaystyle{ \vert\psi\rangle }[/math] through a noisy channel [math]\displaystyle{ \mathcal E }[/math]. Let us moreover assume that this channel either flips the state of the qubit, with probability [math]\displaystyle{ p }[/math], or leaves it unchanged. The action of [math]\displaystyle{ \mathcal E }[/math] on a general input [math]\displaystyle{ \rho }[/math] can therefore be written as [math]\displaystyle{ \mathcal E(\rho) = (1-p) \rho + p\ X\rho X }[/math].

Let [math]\displaystyle{ |\psi\rangle = \alpha_0|0\rangle + \alpha_1|1\rangle }[/math] be the quantum state to be transmitted. With no error correcting protocol in place, the transmitted state will be correctly transmitted with probability [math]\displaystyle{ 1-p }[/math]. We can however improve on this number by encoding the state into a greater number of qubits, in such a way that errors in the corresponding logical qubits can be detected and corrected. In the case of the simple three-qubit repetition code, the encoding consists in the mappings [math]\displaystyle{ \vert0\rangle\rightarrow\vert0_{\rm L}\rangle\equiv\vert000\rangle }[/math] and [math]\displaystyle{ \vert1\rangle\rightarrow\vert1_{\rm L}\rangle\equiv\vert111\rangle }[/math]. The input state [math]\displaystyle{ \vert\psi\rangle }[/math] is encoded into the state [math]\displaystyle{ \vert\psi'\rangle = \alpha_0 \vert000\rangle + \alpha_1 \vert111\rangle }[/math]. This mapping can be realized for example using two CNOT gates, entangling the system with two ancillary qubits initialized in the state [math]\displaystyle{ \vert0\rangle }[/math]. The encoded state [math]\displaystyle{ \vert\psi'\rangle }[/math] is what is now passed through the noisy channel.

The channel acts on [math]\displaystyle{ \vert\psi'\rangle }[/math] by flipping some subset (possibly empty) of its qubits. No qubit is flipped with probability [math]\displaystyle{ (1-p)^3 }[/math], a single qubit is flipped with probability [math]\displaystyle{ 3p(1-p)^2 }[/math], two qubits are flipped with probability [math]\displaystyle{ 3p^2(1-p) }[/math], and all three qubits are flipped with probability [math]\displaystyle{ p^3 }[/math]. Note that a further assumption about the channel is made here: we assume that [math]\displaystyle{ \mathcal E }[/math] acts equally and independently on each of the three qubits in which the state is now encoded. The problem is now how to detect and correct such errors, while not corrupting the transmitted state.

Comparison of output minimum fidelities, with (red) and without (blue) error correcting via the three qubit bit flip code. Notice how, for [math]\displaystyle{ p\le 1/2 }[/math], the error correction scheme improves the fidelity.

Let us assume for simplicity that [math]\displaystyle{ p }[/math] is small enough that the probability of more than a single qubit being flipped is negligible. One can then detect whether a qubit was flipped, without also querying for the values being transmitted, by asking whether one of the qubits differs from the others. This amounts to performing a measurement with four different outcomes, corresponding to the following four projective measurements:[math]\displaystyle{ \begin{align} P_0 &=|000\rangle\langle000|+|111\rangle\langle111|, \\ P_1 &=|100\rangle\langle100|+|011\rangle\langle011|, \\ P_2 &=|010\rangle\langle010|+|101\rangle\langle101|, \\ P_3 &=|001\rangle\langle001|+|110\rangle\langle110|. \end{align} }[/math]This reveals which qubits are different from the others, without at the same time giving information about the state of the qubits themselves. If the outcome corresponding to [math]\displaystyle{ P_0 }[/math] is obtained, no correction is applied, while if the outcome corresponding to [math]\displaystyle{ P_i }[/math] is observed, then the Pauli X gate is applied to the [math]\displaystyle{ i }[/math]-th qubit. Formally, this correcting procedure corresponds to the application of the following map to the output of the channel: [math]\displaystyle{ \mathcal E_{\operatorname{corr}}(\rho)=P_0\rho P_0 + \sum_{i=1}^3 X_i P_i \rho\, P_i X_i. }[/math]

Note that, while this procedure perfectly corrects the output when zero or one flips are introduced by the channel, if more than one qubit is flipped then the output is not properly corrected. For example, if the first and second qubits are flipped, then the syndrome measurement gives the outcome [math]\displaystyle{ P_3 }[/math], and the third qubit is flipped, instead of the first two. To assess the performance of this error-correcting scheme for a general input we can study the fidelity [math]\displaystyle{ F(\psi') }[/math] between the input [math]\displaystyle{ \vert\psi'\rangle }[/math] and the output [math]\displaystyle{ \rho_{\operatorname{out}}\equiv\mathcal E_{\operatorname{corr}}(\mathcal E(\vert\psi'\rangle\langle\psi'\vert)) }[/math]. Being the output state [math]\displaystyle{ \rho_{\operatorname{out}} }[/math] correct when no more than one qubit is flipped, which happens with probability [math]\displaystyle{ (1-p)^3 + 3p(1-p)^2 }[/math], we can write it as [math]\displaystyle{ [(1-p)^3+3p(1-p)^2]\,\vert\psi'\rangle\langle\psi'\vert + (...) }[/math], where the dots denote components of [math]\displaystyle{ \rho_{\operatorname{out}} }[/math] resulting from errors not properly corrected by the protocol. It follows that [math]\displaystyle{ F(\psi')=\langle\psi'\vert\rho_{\operatorname{out}}\vert\psi'\rangle\ge (1-p)^3 + 3p(1-p)^2=1-3p^2+2p^3. }[/math]This fidelity is to be compared with the corresponding fidelity obtained when no error-correcting protocol is used, which was shown before to equal [math]\displaystyle{ {1-p} }[/math]. A little algebra then shows that the fidelity after error correction is greater than the one without for [math]\displaystyle{ p\lt 1/2 }[/math]. Note that this is consistent with the working assumption that was made while deriving the protocol (of [math]\displaystyle{ p }[/math] being small enough).

Sign flip code

Quantum circuit of the phase flip code

Flipped bits are the only kind of error in classical computer, but there is another possibility of an error with quantum computers, the sign flip. Through the transmission in a channel the relative sign between [math]\displaystyle{ |0\rangle }[/math] and [math]\displaystyle{ |1\rangle }[/math] can become inverted. For instance, a qubit in the state [math]\displaystyle{ |-\rangle=(|0\rangle-|1\rangle)/\sqrt{2} }[/math] may have its sign flip to [math]\displaystyle{ |+\rangle=(|0\rangle+|1\rangle)/\sqrt{2}. }[/math]

The original state of the qubit [math]\displaystyle{ |\psi\rangle = \alpha_0|0\rangle+\alpha_1|1\rangle }[/math] will be changed into the state [math]\displaystyle{ |\psi'\rangle = \alpha_0|{+}{+}{+}\rangle+\alpha_1|{-}{-}{-}\rangle. }[/math]

In the Hadamard basis, bit flips become sign flips and sign flips become bit flips. Let [math]\displaystyle{ E_\text{phase} }[/math] be a quantum channel that can cause at most one phase flip. Then the bit flip code from above can recover [math]\displaystyle{ |\psi\rangle }[/math] by transforming into the Hadamard basis before and after transmission through [math]\displaystyle{ E_\text{phase} }[/math].

Shor code

The error channel may induce either a bit flip, a sign flip (i.e., a phase flip), or both. It is possible to correct for both types of errors on any one qubit using a QEC code, which can be done using the Shor code published in 1995. This is equivalent to saying the Shor code corrects arbitrary single-qubit errors.

Quantum circuit to encode a single logical qubit with the Shor code and then perform bit flip error correction on each of the three blocks.

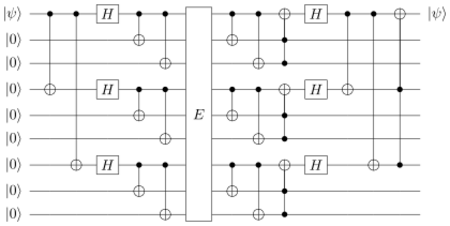
Let [math]\displaystyle{ E }[/math] be a quantum channel that can arbitrarily corrupt a single qubit. The 1st, 4th and 7th qubits are for the sign flip code, while the three groups of qubits (1,2,3), (4,5,6), and (7,8,9) are designed for the bit flip code. With the Shor code, a qubit state [math]\displaystyle{ |\psi\rangle=\alpha_0|0\rangle+\alpha_1|1\rangle }[/math] will be transformed into the product of 9 qubits [math]\displaystyle{ |\psi'\rangle=\alpha_0|0_S\rangle+\alpha_1|1_S\rangle }[/math], where [math]\displaystyle{ |0_{\rm S}\rangle=\frac{1}{2\sqrt{2}}(|000\rangle + |111\rangle) \otimes (|000\rangle + |111\rangle ) \otimes (|000\rangle + |111\rangle) }[/math] [math]\displaystyle{ |1_{\rm S}\rangle=\frac{1}{2\sqrt{2}}(|000\rangle - |111\rangle) \otimes (|000\rangle - |111\rangle) \otimes (|000\rangle - |111\rangle) }[/math]

If a bit flip error happens to a qubit, the syndrome analysis will be performed on each block of qubits (1,2,3), (4,5,6), and (7,8,9) to detect and correct at most one bit flip error in each block.

If the three bit flip group (1,2,3), (4,5,6), and (7,8,9) are considered as three inputs, then the Shor code circuit can be reduced as a sign flip code. This means that the Shor code can also repair a sign flip error for a single qubit.

The Shor code also can correct for any arbitrary errors (both bit flip and sign flip) to a single qubit. If an error is modeled by a unitary transform U, which will act on a qubit [math]\displaystyle{ |\psi\rangle }[/math], then [math]\displaystyle{ U }[/math] can be described in the form [math]\displaystyle{ U = c_0 I + c_1 X + c_2 Y + c_3 Z }[/math] where [math]\displaystyle{ c_0 }[/math],[math]\displaystyle{ c_1 }[/math],[math]\displaystyle{ c_2 }[/math], and [math]\displaystyle{ c_3 }[/math] are complex constants, I is the identity, and the Pauli matrices are given by [math]\displaystyle{ \begin{align} X &= \begin{pmatrix} 0&1\\1&0 \end{pmatrix} ; \\ Y &= \begin{pmatrix} 0&-i\\i&0 \end{pmatrix} ; \\ Z &= \begin{pmatrix} 1&0\\0&-1 \end{pmatrix} . \end{align} }[/math]

If U is equal to I, then no error occurs. If [math]\displaystyle{ U=X }[/math], a bit flip error occurs. If [math]\displaystyle{ U=Z }[/math], a sign flip error occurs. If [math]\displaystyle{ U=iY }[/math] then both a bit flip error and a sign flip error occur. In other words, the Shor code can correct any combination of bit or phase errors on a single qubit.

Bosonic codes

Several proposals have been made for storing error-correctable quantum information in bosonic modes. Unlike a two-level system, a quantum harmonic oscillator has infinitely many energy levels in a single physical system. Codes for these systems include cat, Gottesman-Kitaev-Preskill (GKP), and binomial codes. One insight offered by these codes is to take advantage of the redundancy within a single system, rather than to duplicate many two-level qubits.

Binomial code

Written in the Fock basis, the simplest binomial encoding is [math]\displaystyle{ |0_{\rm L}\rangle=\frac{|0\rangle+|4\rangle}{\sqrt{2}},\quad |1_{\rm L}\rangle=|2\rangle, }[/math] where the subscript L indicates a "logically encoded" state. Then if the dominant error mechanism of the system is the stochastic application of the bosonic lowering operator [math]\displaystyle{ \hat{a}, }[/math] the corresponding error states are [math]\displaystyle{ |3\rangle }[/math] and [math]\displaystyle{ |1\rangle, }[/math] respectively. Since the codewords involve only even photon number, and the error states involve only odd photon number, errors can be detected by measuring the photon number parity of the system. Measuring the odd parity will allow correction by application of an appropriate unitary operation without knowledge of the specific logical state of the qubit. However, the particular binomial code above is not robust to two-photon loss.

Cat code

Schrödinger cat states, superpositions of coherent states, can also be used as logical states for error correction codes. Cat code, realized by Ofek et al. in 2016, defined two sets of logical states: [math]\displaystyle{ \{|0^+_L\rangle, |1^+_L\rangle\} }[/math] and [math]\displaystyle{ \{|0^-_L\rangle, |1^-_L\rangle\} }[/math], where each of the states is a superposition of coherent state as follows

[math]\displaystyle{ \begin{aligned} |0^+_L\rangle& \equiv |\alpha\rangle + |-\alpha\rangle, \\ |1^+_L\rangle& \equiv |i\alpha\rangle + |-i\alpha\rangle, \\ |0^-_L\rangle& \equiv |\alpha\rangle - |-\alpha\rangle, \\ |1^-_L\rangle& \equiv |i\alpha\rangle - |-i\alpha\rangle. \end{aligned} }[/math]

Those two sets of states differ from the photon number parity, as states denoted with [math]\displaystyle{ ^+ }[/math] only occupy even photon number states and states with [math]\displaystyle{ ^- }[/math] indicate they have odd parity. Similar to the binomial code, if the dominant error mechanism of the system is the stochastic application of the bosonic lowering operator [math]\displaystyle{ \hat{a} }[/math], the error takes the logical states from the even parity subspace to the odd one, and vice versa. Single-photon-loss errors can therefore be detected by measuring the photon number parity operator [math]\displaystyle{ \exp(i\pi \hat{a}^\dagger\hat{a}) }[/math] using a dispersively coupled ancillary qubit.

Still, cat qubits are not protected against two-photon loss [math]\displaystyle{ \hat{a}^2 }[/math], dephasing noise [math]\displaystyle{ \hat{a}^\dagger\hat{a} }[/math], photon-gain error [math]\displaystyle{ \hat{a}^\dagger }[/math], etc.

General codes

In general, a quantum code for a quantum channel [math]\displaystyle{ \mathcal{E} }[/math] is a subspace [math]\displaystyle{ \mathcal{C} \subseteq \mathcal{H} }[/math], where [math]\displaystyle{ \mathcal{H} }[/math] is the state Hilbert space, such that there exists another quantum channel [math]\displaystyle{ \mathcal{R} }[/math] with [math]\displaystyle{ (\mathcal{R} \circ \mathcal{E})(\rho) = \rho \quad \forall \rho = P_{\mathcal{C}}\rho P_{\mathcal{C}}, }[/math] where [math]\displaystyle{ P_{\mathcal{C}} }[/math] is the orthogonal projection onto [math]\displaystyle{ \mathcal{C} }[/math]. Here [math]\displaystyle{ \mathcal{R} }[/math] is known as the correction operation.

A non-degenerate code is one for which different elements of the set of correctable errors produce linearly independent results when applied to elements of the code. If distinct of the set of correctable errors produce orthogonal results, the code is considered pure.

Models

Over time, researchers have come up with several codes:

• Peter Shor's 9-qubit-code, a.k.a. the Shor code, encodes 1 logical qubit in 9 physical qubits and can correct for arbitrary errors in a single qubit.
• Andrew Steane found a code that does the same with 7 instead of 9 qubits, see Steane code.
• Raymond Laflamme and collaborators found a class of 5-qubit codes that do the same, which also have the property of being fault-tolerant. A 5-qubit code is the smallest possible code that protects a single logical qubit against single-qubit errors.
• A generalisation of the technique used by Steane, to develop the 7-qubit code from the classical [7, 4] Hamming code, led to the construction of an important class of codes called the CSS codes, named for their inventors: Robert Calderbank, Peter Shor and Andrew Steane. According to the quantum Hamming bound, encoding a single logical qubit and providing for arbitrary error correction in a single qubit requires a minimum of 5 physical qubits.
• A more general class of codes (encompassing the former) are the stabilizer codes discovered by Daniel Gottesman, and by Robert Calderbank, Eric Rains, Peter Shor, and N. J. A. Sloane; these are also called additive codes.
• Two dimensional Bacon–Shor codes are a family of codes parameterized by integers m and n. There are nm qubits arranged in a square lattice.
• A newer idea is Alexei Kitaev's topological quantum codes and the more general idea of a topological quantum computer.
• Todd Brun, Igor Devetak, and Min-Hsiu Hsieh also constructed the entanglement-assisted stabilizer formalism as an extension of the standard stabilizer formalism that incorporates quantum entanglement shared between a sender and a receiver.

That these codes allow indeed for quantum computations of arbitrary length is the content of the quantum threshold theorem, found by Michael Ben-Or and Dorit Aharonov, which asserts that you can correct for all errors if you concatenate quantum codes such as the CSS codes—i.e. re-encode each logical qubit by the same code again, and so on, on logarithmically many levels—provided that the error rate of individual quantum gates is below a certain threshold; as otherwise, the attempts to measure the syndrome and correct the errors would introduce more new errors than they correct for.

As of late 2004, estimates for this threshold indicate that it could be as high as 1–3%, provided that there are sufficiently many qubits available.

Experimental realization

There have been several experimental realizations of CSS-based codes. The first demonstration was with nuclear magnetic resonance qubits. Subsequently, demonstrations have been made with linear optics, trapped ions, and superconducting (transmon) qubits.

In 2016 for the first time the lifetime of a quantum bit was prolonged by employing a QEC code. The error-correction demonstration was performed on Schrodinger-cat states encoded in a superconducting resonator, and employed a quantum controller capable of performing real-time feedback operations including read-out of the quantum information, its analysis, and the correction of its detected errors. The work demonstrated how the quantum-error-corrected system reaches the break-even point at which the lifetime of a logical qubit exceeds the lifetime of the underlying constituents of the system (the physical qubits).

Other error correcting codes have also been implemented, such as one aimed at correcting for photon loss, the dominant error source in photonic qubit schemes.

In 2021, an entangling gate between two logical qubits encoded in topological quantum error-correction codes has first been realized using 10 ions in a trapped-ion quantum computer. 2021 also saw the first experimental demonstration of fault-tolerant Bacon-Shor code in a single logical qubit of a trapped-ion system, i.e. a demonstration for which the addition of error correction is able to suppress more errors than is introduced by the overhead required to implement the error correction as well as fault tolerant Steane code.

In 2022, researchers at the University of Innsbruck have demonstrated a fault-tolerant universal set of gates on two logical qubits in a trapped-ion quantum computer. They have performed a logical two-qubit controlled-NOT gate between two instances of the seven-qubit colour code, and fault-tolerantly prepared a logical magic state.

In February 2023 researchers at Google claimed to have decreased quantum errors by increasing the qubit number in experiments, they used a fault tolerant surface code measuring an error rate of 3.028% and 2.914% for a distance-3 qubit array and a distance-5 qubit array respectively.

Quantum error-correction without encoding and parity-checks

Also in 2022, research at University of Engineering and Technology Lahore demonstrated error-cancellation by inserting single-qubit Z-axis rotation gates into strategically chosen locations of the superconductor quantum circuits. The scheme has been shown to effectively correct errors that would otherwise rapidly add up under constructive interference of coherent noise. This is a circuit-level calibration scheme that traces deviations (e.g. sharp dips or notches) in the decoherence curve to detect and localize the coherent error, but does not require encoding or parity measurements. However, further investigation is needed to establish the effectiveness of this method for the incoherent noise.

See also

• Error detection and correction
• Soft error

Further reading

• Daniel Lidar and Todd Brun, ed (2013). Quantum Error Correction. Cambridge University Press. 
• La Guardia, Giuliano Gadioli, ed (2020). Quantum Error Correction: Symmetric, Asymmetric, Synchronizable, and Convolutional Codes. Springer Nature. 
• Frank Gaitan (2008). Quantum Error Correction and Fault Tolerant Quantum Computing. Taylor & Francis. 
• Freedman, Michael H.; Meyer, David A.; Luo, Feng (2002). "Z₂-Systolic freedom and quantum codes". Mathematics of quantum computation. Comput. Math. Ser.. Boca Raton, FL: Chapman & Hall/CRC. pp. 287–320. 
• Freedman, Michael H.; Meyer, David A. (1998). "Projective plane and planar quantum codes". Found. Comput. Math. 2001 (3): 325–332. Bibcode: 1998quant.ph.10055F. 

External links

• "Breakthrough in quantum error correction could lead to large-scale quantum computers". http://hadamard.com/news/index.php?title=Breakthrough_in_quantum_error_correction_could_lead_to_large-scale_quantum_computers.