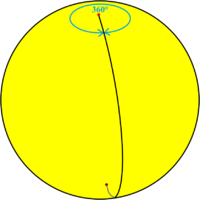
Spherical lune
In spherical geometry, a spherical lune (or biangle) is an area on a sphere bounded by two half great circles which meet at antipodal points.[1] It is an example of a digon, {2}θ, with dihedral angle θ.[2] The word "lune" derives from luna, the Latin word for Moon.
Properties
Great circles are the largest possible circles (circumferences) of a sphere; each one divides the surface of the sphere into two equal halves. Two great circles always intersect at two polar opposite points.
Common examples of great circles are lines of longitude (meridians) on a sphere, which meet at the north and south poles.
A spherical lune has two planes of symmetry. It can be bisected into two lunes of half the angle, or it can be bisected by an equatorial line into two right spherical triangles.
Surface area
The surface area of a spherical lune is 2θ R2, where R is the radius of the sphere and θ is the dihedral angle in radians between the two half great circles.
When this angle equals 2π radians (360°) — i.e., when the second half great circle has moved a full circle, and the lune in between covers the sphere as a spherical monogon — the area formula for the spherical lune gives 4πR2, the surface area of the sphere.
Examples
A hosohedron is a tessellation of the sphere by lunes. A n-gonal regular hosohedron, {2,n} has n equal lunes of π/n radians. An n-hosohedron has dihedral symmetry Dnh, [n,2], (*22n) of order 4n. Each lune individually has cyclic symmetry C2v, [2], (*22) of order 4.
Each hosohedra can be divided by an equatorial bisector into two equal spherical triangles.
| n | 2 | 3 | 4 | 5 | 6 | ... |
|---|---|---|---|---|---|---|
| Hosohedra | 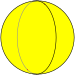
|
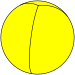
|
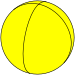
|
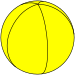
|
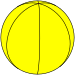
|
... |
| Bipyramidal tiling |

|
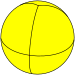
|

|
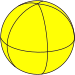
|

|
... |
Astronomy
The visibly lighted portion of the Moon visible from the Earth is a spherical lune. The first of the two intersecting great circles is the terminator between the sunlit half of the Moon and the dark half. The second great circle is a terrestrial terminator that separates the half visible from the Earth from the unseen half. The spherical lune is a lighted crescent shape seen from Earth.
n-sphere lunes

Lunes can be defined on higher dimensional spheres as well.
In 4-dimensions a 3-sphere is a generalized sphere. It can contain regular digon lunes as {2}θ,φ, where θ and φ are two dihedral angles.
For example, a regular hosotope {2,p,q} has digon faces, {2}2π/p,2π/q, where its vertex figure is a spherical platonic solid, {p,q}. Each vertex of {p,q} defines an edge in the hosotope and adjacent pairs of those edges define lune faces. Or more specifically, the regular hosotope {2,4,3}, has 2 vertices, 8 180° arc edges in a cube, {4,3}, vertex figure between the two vertices, 12 lune faces, {2}π/4,π/3, between pairs of adjacent edges, and 6 hosohedral cells, {2,p}π/3.
References
- ↑ Davis, Elwyn H. (1999). "Area of spherical triangles". The Mathematics Teacher 92 (2): 150-153. doi:10.5951/MT.92.2.0150.
- ↑ Weisstein, Eric W.. "Spherical Lune". http://mathworld.wolfram.com/SphericalLune.html.
- Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, Florida: CRC Press, p. 130, 1987.
- Harris, J. W. and Stocker, H. "Spherical Wedge." §4.8.6 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 108, 1998.
- Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, p. 262, 1989.
 |