Biology:Voltage clamp

The voltage clamp is an experimental method used by electrophysiologists to measure the ion currents through the membranes of excitable cells, such as neurons, while holding the membrane voltage at a set level.[1] A basic voltage clamp will iteratively measure the membrane potential, and then change the membrane potential (voltage) to a desired value by adding the necessary current. This "clamps" the cell membrane at a desired constant voltage, allowing the voltage clamp to record what currents are delivered. Because the currents applied to the cell must be equal to (and opposite in charge to) the current going across the cell membrane at the set voltage, the recorded currents indicate how the cell reacts to changes in membrane potential.[2] Cell membranes of excitable cells contain many different kinds of ion channels, some of which are voltage-gated. The voltage clamp allows the membrane voltage to be manipulated independently of the ionic currents, allowing the current–voltage relationships of membrane channels to be studied.[3]
History
The concept of the voltage clamp is attributed to Kenneth Cole[4] and George Marmont[5] in the spring of 1947.[6] They inserted an internal electrode into the giant axon of a squid and began to apply a current. Cole discovered that it was possible to use two electrodes and a feedback circuit to keep the cell's membrane potential at a level set by the experimenter.
Cole developed the voltage clamp technique before the era of microelectrodes, so his two electrodes consisted of fine wires twisted around an insulating rod. Because this type of electrode could be inserted into only the largest cells, early electrophysiological experiments were conducted almost exclusively on squid axons.
Squids squirt jets of water when they need to move quickly, as when escaping a predator. To make this escape as fast as possible, they have an axon that can reach 1 mm in diameter (signals propagate more quickly down large axons). The squid giant axon was the first preparation that could be used to voltage clamp a transmembrane current, and it was the basis of Hodgkin and Huxley's pioneering experiments on the properties of the action potential.[6]
Alan Hodgkin realized that, to understand ion flux across the membrane, it was necessary to eliminate differences in membrane potential.[7] Using experiments with the voltage clamp, Hodgkin and Andrew Huxley published 5 papers in the summer of 1952 describing how ionic currents give rise to the action potential.[8] The final paper proposed the Hodgkin–Huxley model which mathematically describes the action potential. The use of voltage clamps in their experiments to study and model the action potential in detail has laid the foundation for electrophysiology; for which they shared the 1963 Nobel Prize in Physiology or Medicine.[7]
Technique
The voltage clamp is a current generator. Transmembrane voltage is recorded through a "voltage electrode", relative to ground, and a "current electrode" passes current into the cell. The experimenter sets a "holding voltage", or "command potential", and the voltage clamp uses negative feedback to maintain the cell at this voltage. The electrodes are connected to an amplifier, which measures membrane potential and feeds the signal into a feedback amplifier. This amplifier also gets an input from the signal generator that determines the command potential, and it subtracts the membrane potential from the command potential (Vcommand – Vm), magnifies any difference, and sends an output to the current electrode. Whenever the cell deviates from the holding voltage, the operational amplifier generates an "error signal", that is the difference between the command potential and the actual voltage of the cell. The feedback circuit passes current into the cell to reduce the error signal to zero. Thus, the clamp circuit produces a current equal and opposite to the ionic current.
Variations of the voltage clamp technique
Two-electrode voltage clamp using microelectrodes
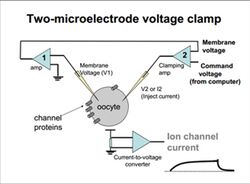
The two-electrode voltage clamp (TEVC) technique is used to study properties of membrane proteins, especially ion channels.[9] Researchers use this method most commonly to investigate membrane structures expressed in Xenopus oocytes. The large size of these oocytes allows for easy handling and manipulability.[10]
The TEVC method utilizes two low-resistance pipettes, one sensing voltage and the other injecting current. The microelectrodes are filled with conductive solution and inserted into the cell to artificially control membrane potential. The membrane acts as a dielectric as well as a resistor, while the fluids on either side of the membrane function as capacitors.[10] The microelectrodes compare the membrane potential against a command voltage, giving an accurate reproduction of the currents flowing across the membrane. Current readings can be used to analyze the electrical response of the cell to different applications.
This technique is favored over single-microelectrode clamp or other voltage clamp techniques when conditions call for resolving large currents. The high current-passing capacity of the two-electrode clamp makes it possible to clamp large currents that are impossible to control with single-electrode patch techniques.[11] The two-electrode system is also desirable for its fast clamp settling time and low noise. However, TEVC is limited in use with regard to cell size. It is effective in larger-diameter oocytes, but more difficult to use with small cells. Additionally, TEVC method is limited in that the transmitter of current must be contained in the pipette. It is not possible to manipulate the intracellular fluid while clamping, which is possible using patch clamp techniques.[2] Another disadvantage involves "space clamp" issues. Cole's voltage clamp used a long wire that clamped the squid axon uniformly along its entire length. TEVC microelectrodes can provide only a spatial point source of current that may not uniformly affect all parts of an irregularly shaped cell.
Dual-cell voltage clamp
The dual-cell voltage clamp technique is a specialized variation of the two electrode voltage clamp, and is only used in the study of gap junction channels.[12] Gap junctions are pores that directly link two cells through which ions and small molecules flow freely. When two cells in which gap junction proteins, typically connexins or innexins, are expressed, either endogenously or via injection of mRNA, a junction channel will form between the cells. Since two cells are present in the system, two sets of electrodes are used. A recording electrode and a current injecting electrode are inserted into each cell, and each cell is clamped individually (each set of electrodes is attached to a separate apparatus, and integration of data is performed by computer). To record junctional conductance, the current is varied in the first cell while the recording electrode in the second cell records any changes in Vm for the second cell only. (The process can be reversed with the stimulus occurring in the second cell and recording occurring in the first cell.) Since no variation in current is being induced by the electrode in the recorded cell, any change in voltage must be induced by current crossing into the recorded cell, through the gap junction channels, from the cell in which the current was varied.[12]
Single-electrode voltage clamp
This category describes a set of techniques in which one electrode is used for voltage clamp. Continuous single-electrode clamp (SEVC-c) technique is often used with patch-clamp recording. Discontinuous single-electrode voltage-clamp (SEVC-d) technique is used with penetrating intracellular recording. This single electrode carries out the functions of both current injection and voltage recording.
Continuous single-electrode clamp (SEVC-c)
The "patch-clamp" technique allows the study of individual ion channels. It uses an electrode with a relatively large tip (> 1 micrometer) that has a smooth surface (rather than a sharp tip). This is a "patch-clamp electrode" (as distinct from a "sharp electrode" used to impale cells). This electrode is pressed against a cell membrane and suction is applied to pull the cell's membrane inside the electrode tip. The suction causes the cell to form a tight seal with the electrode (a "gigaohm seal", as the resistance is more than a gigaohm).
SEV-c has the advantage that you can record from small cells that would be impossible to impale with two electrodes. However:
- Microelectrodes are imperfect conductors; in general, they have a resistance of more than a million ohms. They rectify (i.e., change their resistance with voltage, often in an irregular manner), they sometimes have unstable resistance if clogged by cell contents. Thus, they will not faithfully record the voltage of the cell, especially when it is changing quickly, nor will they faithfully pass current.
- Voltage and current errors: SEV-c circuitry does not actually measure the voltage of the cell being clamped (as does a two-electrode clamp). The patch-clamp amplifier is like a two-electrode clamp, except the voltage measuring and current passing circuits are connected (in the two-electrode clamp, they are connected through the cell). The electrode is attached to a wire that contacts the current/voltage loop inside the amplifier. Thus, the electrode has only an indirect influence on the feedback circuit. The amplifier reads only the voltage at the top of the electrode, and feeds back current to compensate. But, if the electrode is an imperfect conductor, the clamp circuitry has only a distorted view of the membrane potential. Likewise, when the circuit passes back current to compensate for that (distorted) voltage, the current will be distorted by the electrode before it reaches the cell. To compensate for this, the electrophysiologist uses the lowest resistance electrode possible, makes sure that the electrode characteristics do not change during an experiment (so the errors will be constant), and avoids recording currents with kinetics likely to be too fast for the clamp to follow accurately. The accuracy of SEV-c goes up the slower and smaller are the voltage changes it is trying to clamp.
- Series resistance errors: The currents passed to the cell must go to ground to complete the circuit. The voltages are recorded by the amplifier relative to ground. When a cell is clamped at its natural resting potential, there is no problem; the clamp is not passing current and the voltage is being generated only by the cell. But, when clamping at a different potential, series resistance errors become a concern; the cell will pass current across its membrane in an attempt to return to its natural resting potential. The clamp amplifier opposes this by passing current to maintain the holding potential. A problem arises because the electrode is between the amplifier and the cell; i.e., the electrode is in series with the resistor that is the cell's membrane. Thus, when passing current through the electrode and the cell, Ohm's law tells us that this will cause a voltage to form across both the cell's and the electrode's resistance. As these resistors are in series, the voltage drops will add. If the electrode and the cell membrane have equal resistances (which they usually do not), and if the experimenter command a 40mV change from the resting potential, the amplifier will pass enough current until it reads that it has achieved that 40mV change. However, in this example, half of that voltage drop is across the electrode. The experimenter thinks he or she has moved the cell voltage by 40 mV, but has moved it only by 20 mV. The difference is the "series resistance error". Modern patch-clamp amplifiers have circuitry to compensate for this error, but these compensate only 70-80% of it. The electrophysiologist can further reduce the error by recording at or near the cell's natural resting potential, and by using as low a resistance electrode as possible.
- Capacitance errors. Microelectrodes are capacitors, and are particularly troublesome because they are non-linear. The capacitance arises because the electrolyte inside the electrode is separated by an insulator (glass) from the solution outside. This is, by definition and function, a capacitor. Worse, as the thickness of the glass changes the farther you get from the tip, the time constant of the capacitor will vary. This produces a distorted record of membrane voltage or current whenever they are changing. Amplifiers can compensate for this, but not entirely because the capacitance has many time-constants. The experimenter can reduce the problem by keeping the cell's bathing solution shallow (exposing less glass surface to liquid) and by coating the electrode with silicone, resin, paint, or another substance that will increase the distance between the inside and outside solutions.
- Space clamp errors. A single electrode is a point source of current. In distant parts of the cell, the current passed through the electrode will be less influential than at nearby parts of the cell. This is particularly a problem when recording from neurons with elaborate dendritic structures. There is nothing one can do about space clamp errors except to temper the conclusions of the experiment.
Discontinuous single-electrode voltage-clamp (SEVC-d)
A single-electrode voltage clamp — discontinuous, or SEVC-d, has some advantages over SEVC-c for whole-cell recording. In this, a different approach is taken for passing current and recording voltage. A SEVC-d amplifier operates on a "time-sharing" basis, so the electrode regularly and frequently switches between passing current and measuring voltage. In effect, there are two electrodes, but each is in operation for only half of the time it is on. The oscillation between the two functions of the single electrode is termed a duty cycle. During each cycle, the amplifier measures the membrane potential and compares it with the holding potential. An operational amplifier measures the difference, and generates an error signal. This current is a mirror image of the current generated by the cell. The amplifier outputs feature sample and hold circuits, so each briefly sampled voltage is then held on the output until the next measurement in the next cycle. To be specific, the amplifier measures voltage in the first few microseconds of the cycle, generates the error signal, and spends the rest of the cycle passing current to reduce that error. At the start of the next cycle, voltage is measured again, a new error signal generated, current passed etc. The experimenter sets the cycle length, and it is possible to sample with periods as low as about 15 microseconds, corresponding to a 67 kHz switching frequency. Switching frequencies lower than about 10 kHz are not sufficient when working with action potentials that are less than 1 millisecond wide. Note that not all discontinuous voltage-clamp amplifier support switching frequencies higher than 10 kHz.[10]
For this to work, the cell capacitance must be higher than the electrode capacitance by at least an order of magnitude. Capacitance slows the kinetics (the rise and fall times) of currents. If the electrode capacitance is much less than that of the cell, then when current is passed through the electrode, the electrode voltage will change faster than the cell voltage. Thus, when current is injected and then turned off (at the end of a duty cycle), the electrode voltage will decay faster than the cell voltage. As soon as the electrode voltage asymptotes to the cell voltage, the voltage can be sampled (again) and the next amount of charge applied. Thus, the frequency of the duty cycle is limited to the speed at which the electrode voltage rises and decays while passing current. The lower the electrode capacitance the faster one can cycle.
SEVC-d has a major advantage over SEVC-c in allowing the experimenter to measure membrane potential, and, as it obviates passing current and measuring voltage at the same time, there is never a series resistance error. The main disadvantages are that the time resolution is limited and the amplifier is unstable. If it passes too much current, so that the goal voltage is over-shot, it reverses the polarity of the current in the next duty cycle. This causes it to undershoot the target voltage, so the next cycle reverses the polarity of the injected current again. This error can grow with each cycle until the amplifier oscillates out of control (“ringing”); this usually results in the destruction of the cell being recorded. The investigator wants a short duty cycle to improve temporal resolution; the amplifier has adjustable compensators that will make the electrode voltage decay faster, but, if these are set too high the amplifier will ring, so the investigator is always trying to “tune” the amplifier as close to the edge of uncontrolled oscillation as possible, in which case small changes in recording conditions can cause ringing. There are two solutions: to “back off” the amplifier settings into a safe range, or to be alert for signs that the amplifier is about to ring.
Mathematical modeling
From the point of view of control theory, the voltage clamp experiment can be described in terms of the application of a high-gain output feedback control law[13] to the neuronal membrane.[14] Mathematically, the membrane voltage can be modeled by a conductance-based model with an input given by the applied current [math]\displaystyle{ I_{app}(t) }[/math] and an output given by the membrane voltage [math]\displaystyle{ V(t) }[/math]. Hodgkin and Huxley's original conductance-based model, which represents a neuronal membrane containing sodium and potassium ion currents, as well as a leak current, is given by the system of ordinary differential equations
[math]\displaystyle{ C_m \frac{dV}{dt} = -\bar{g}_{\text{K}} n^4 (V-V_\text{K}) -\bar{g}_{\text{Na}} m^3 h (V-V_\text{Na}) - \bar{g}_{\text{L}} (V-V_L) + I_{app} }[/math]
[math]\displaystyle{ \frac{dp}{dt} = \alpha_p(V)(1-p) - \beta_p(V)p, \quad p=m,n,h }[/math]
where [math]\displaystyle{ C_m }[/math] is the membrane capacitance, [math]\displaystyle{ \bar{g}_{\text{Na}} }[/math], [math]\displaystyle{ \bar{g}_{\text{K}} }[/math] and [math]\displaystyle{ \bar{g}_{\text{L}} }[/math]are maximal conductances, [math]\displaystyle{ V_{\text{Na}} }[/math], [math]\displaystyle{ V_{\text{K}} }[/math] and [math]\displaystyle{ V_{\text{L}} }[/math] are reversal potentials, [math]\displaystyle{ \alpha_p }[/math] and [math]\displaystyle{ \beta_p }[/math] are ion channel voltage-dependent rate constants, and the state variables [math]\displaystyle{ m }[/math], [math]\displaystyle{ h }[/math], and [math]\displaystyle{ n }[/math] are ion channel gating variables.
It is possible to rigorously show that the feedback law
[math]\displaystyle{ I_{app}(t) = k(V_{\text{ref}} - V(t)) }[/math]
drives the membrane voltage [math]\displaystyle{ V(t) }[/math] arbitrarily close to the reference voltage [math]\displaystyle{ V_{\text{ref}} }[/math] as the gain [math]\displaystyle{ k\gt 0 }[/math] is increased to an arbitrarily large value.[14] This fact, which is by no means a general property of dynamical systems (a high-gain can, in general, lead to instability[15]), is a consequence of the structure and the properties of the conductance-based model above. In particular, the dynamics of each gating variable [math]\displaystyle{ p=m,h,n }[/math], which are driven by [math]\displaystyle{ V }[/math], verify the strong stability property of exponential contraction.[14][16]
References
- ↑ (in en) Encyclopedia of Computational Neuroscience. Springer New York. 2014. pp. 1–5. doi:10.1007/978-1-4614-7320-6_137-2. ISBN 9781461473206.
- ↑ 2.0 2.1 "Voltage clamp methods for the study of membrane currents and SR Ca(2+) release in adult skeletal muscle fibres". Progress in Biophysics and Molecular Biology 108 (3): 98–118. April 2012. doi:10.1016/j.pbiomolbio.2012.01.001. PMID 22306655.
- ↑ Principles of Neural Science (4th ed.). New York: McGraw-Hill. 2000. pp. 152–3. ISBN 978-0-8385-7701-1.
- ↑ Neuroscience: Exploring the Brain (3rd ed.). Philadelphia, Baltimore: Lippincott Williams & Wilkins. 2006. p. 84. LCC QP355.2.B42. ISBN 978-0-7817-6003-4. https://books.google.com/books?id=75NgwLzueikC&pg=PA84.
- ↑ "A Brief history of Computational Neuroscience". Simulations with NEURON. Duke University. 1994. http://neuron.duke.edu/userman/2/pioneer.html.
- ↑ 6.0 6.1 Andrew Huxley, 1996, "Kenneth Sterward Cole 1900 – 1984, A biographical Memoir" National Academy of Sciences. (Washington D.C.)
- ↑ 7.0 7.1 "From overshoot to voltage clamp". Trends in Neurosciences 25 (11): 553–8. November 2002. doi:10.1016/S0166-2236(02)02280-4. PMID 12392929.
- ↑ Vandenberg, J. I. and S. G. Waxman (2012). "Hodgkin and Huxley and the basis for electrical signalling: a remarkable legacy still going strong." J. Physiol. (Oxford, U. K.) 590(11): 2569–2570.
- ↑ "Two-electrode voltage clamp". Ion Channels. Methods in Molecular Biology. 998. 2013. pp. 79–89. doi:10.1007/978-1-62703-351-0_6. ISBN 978-1-62703-350-3.
- ↑ 10.0 10.1 10.2 "The use of control theory for the design of voltage clamp systems: a simple and standardized procedure for evaluating system parameters". Journal of Neuroscience Methods 109 (2): 97–109. August 2001. doi:10.1016/S0165-0270(01)00385-5. PMID 11513944.
- ↑ "Chloride currents from the transverse tubular system in adult mammalian skeletal muscle fibers". The Journal of General Physiology 137 (1): 21–41. January 2011. doi:10.1085/jgp.201010496. PMID 21149546.
- ↑ 12.0 12.1 "Quantitative analysis of dual whole-cell voltage-clamp determination of gap junctional conductance". Pflügers Archiv 436 (1): 141–51. June 1998. doi:10.1007/s004240050615. PMID 9560458.
- ↑ "High-gain feedback in non-linear control systems". International Journal of Control 42 (6): 1369–1385. December 1985. doi:10.1080/00207178508933431.
- ↑ 14.0 14.1 14.2 "Feedback identification of conductance-based models" (in en). Automatica 123: 109297. 2021. doi:10.1016/j.automatica.2020.109297. https://pure.tue.nl/ws/files/182722777/1_s2.0_S0005109820304969_main.pdf.
- ↑ "Control Systems/Gain - Wikibooks, open books for an open world" (in en). https://en.wikibooks.org/wiki/Control_Systems/Gain.
- ↑ "On Contraction Analysis for Non-linear Systems" (in en). Automatica 34 (6): 683–696. 1998. doi:10.1016/S0005-1098(98)00019-3.
Further reading
- "Bioelectricity". The Axon Guide for Electrophysiology & Biophysics Laboratory Techniques. Axon Instruments. 1993. pp. 1–16. OCLC 248830666. http://stg.rutgers.edu/stg_lab/protocols/The%20axon%20Guide.pdf.
 |