Square packing
Square packing is a packing problem where the objective is to determine how many congruent squares can be packed into some larger shape, often a square or circle.
Square packing in a square
Square packing in a square is the problem of determining the maximum number of unit squares (squares of side length one) that can be packed inside a larger square of side length [math]\displaystyle{ a }[/math]. If [math]\displaystyle{ a }[/math] is an integer, the answer is [math]\displaystyle{ a^2, }[/math] but the precise – or even asymptotic – amount of unfilled space for an arbitrary non-integer [math]\displaystyle{ a }[/math] is an open question.[1]
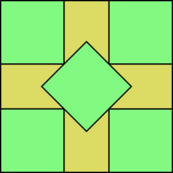
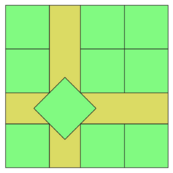
The smallest value of [math]\displaystyle{ a }[/math] that allows the packing of [math]\displaystyle{ n }[/math] unit squares is known when [math]\displaystyle{ n }[/math] is a perfect square (in which case it is [math]\displaystyle{ \sqrt{n} }[/math]), as well as for [math]\displaystyle{ n={} }[/math]2, 3, 5, 6, 7, 8, 10, 13, 14, 15, 24, 34, 35, 46, 47, and 48. For most of these numbers (with the exceptions only of 5 and 10), the packing is the natural one with axis-aligned squares, and [math]\displaystyle{ a }[/math] is [math]\displaystyle{ \lceil\sqrt{n}\,\rceil }[/math], where [math]\displaystyle{ \lceil\,\ \rceil }[/math] is the ceiling (round up) function.[2][3] The figure shows the optimal packings for 5 and 10 squares, the two smallest numbers of squares for which the optimal packing involves tilted squares.[4][5]
The smallest unresolved case involves packing 11 unit squares into a larger square. 11 unit squares cannot be packed in a square of side length less than [math]\displaystyle{ \textstyle 2+2\sqrt{4/5} \approx 3.789 }[/math]. By contrast, the tightest known packing of 11 squares is inside a square of side length approximately 3.877084 found by Walter Trump.[6][4]
Asymptotic results
| Unsolved problem in mathematics: What is the asymptotic growth rate of wasted space for square packing in a half-integer square? (more unsolved problems in mathematics)
|
For larger values of the side length [math]\displaystyle{ a }[/math], the exact number of unit squares that can pack an [math]\displaystyle{ a\times a }[/math] square remains unknown. It is always possible to pack a [math]\displaystyle{ \lfloor a\rfloor \!\times\! \lfloor a\rfloor }[/math] grid of axis-aligned unit squares, but this may leave a large area, approximately [math]\displaystyle{ 2a(a-\lfloor a\rfloor) }[/math], uncovered and wasted.[4] Instead, Paul Erdős and Ronald Graham showed that for a different packing by tilted unit squares, the wasted space could be significantly reduced to [math]\displaystyle{ o(a^{7/11}) }[/math] (here written in little o notation).[7] Later, Graham and Fan Chung further reduced the wasted space to [math]\displaystyle{ O(a^{3/5}) }[/math].[8] However, as Klaus Roth and Bob Vaughan proved, all solutions must waste space at least [math]\displaystyle{ \Omega\bigl(a^{1/2}(a-\lfloor a\rfloor)\bigr) }[/math]. In particular, when [math]\displaystyle{ a }[/math] is a half-integer, the wasted space is at least proportional to its square root.[9] The precise asymptotic growth rate of the wasted space, even for half-integer side lengths, remains an open problem.[1]
Some numbers of unit squares are never the optimal number in a packing. In particular, if a square of size [math]\displaystyle{ a\times a }[/math] allows the packing of [math]\displaystyle{ n^2-2 }[/math] unit squares, then it must be the case that [math]\displaystyle{ a\ge n }[/math] and that a packing of [math]\displaystyle{ n^2 }[/math] unit squares is also possible.[2]
Square packing in a circle
Square packing in a circle is a related problem of packing n unit squares into a circle with radius as small as possible. For this problem, good solutions are known for n up to 35. Here are minimum solutions for n up to 12:[10]
| Number of squares | Circle radius |
|---|---|
| 1 | 0.707... |
| 2 | 1.118... |
| 3 | 1.288... |
| 4 | 1.414... |
| 5 | 1.581... |
| 6 | 1.688... |
| 7 | 1.802... |
| 8 | 1.978... |
| 9 | 2.077... |
| 10 | 2.121... |
| 11 | 2.214... |
| 12 | 2.236... |
See also
References
- ↑ 1.0 1.1 Brass, Peter; Moser, William; Pach, János (2005), Research Problems in Discrete Geometry, New York: Springer, p. 45, ISBN 978-0387-23815-9, https://books.google.com/books?id=WehCspo0Qa0C&pg=PA45
- ↑ 2.0 2.1 Kearney, Michael J.; Shiu, Peter (2002), "Efficient packing of unit squares in a square", Electronic Journal of Combinatorics 9 (1): Research Paper 14, 14 pp., http://www.combinatorics.org/Volume_9/Abstracts/v9i1r14.html
- ↑ Bentz, Wolfram (2010), "Optimal packings of 13 and 46 unit squares in a square", The Electronic Journal of Combinatorics 17 (R126), doi:10.37236/398, https://www.combinatorics.org/Volume_17/Abstracts/v17i1r126.html
- ↑ 4.0 4.1 4.2 Friedman, Erich (2009), "Packing unit squares in squares: a survey and new results", Electronic Journal of Combinatorics: Dynamic Survey 7, http://www.combinatorics.org/ojs/index.php/eljc/article/view/DS7
- ↑ Stromquist, Walter (2003), "Packing 10 or 11 unit squares in a square", Electronic Journal of Combinatorics 10: Research Paper 8, http://www.combinatorics.org/Volume_10/Abstracts/v10i1r8.html
- ↑ Gensane, Thierry; Ryckelynck, Philippe (2005), "Improved dense packings of congruent squares in a square", Discrete & Computational Geometry 34 (1): 97–109, doi:10.1007/s00454-004-1129-z
- ↑ "On packing squares with equal squares", Journal of Combinatorial Theory, Series A 19: 119–123, 1975, doi:10.1016/0097-3165(75)90099-0, http://www.math.ucsd.edu/~sbutler/ron/75_06_squares.pdf
- ↑ "Efficient packings of unit squares in a large square", Discrete & Computational Geometry 64 (3): 690–699, 2020, doi:10.1007/s00454-019-00088-9, https://www.math.ucsd.edu/~fan/wp/spacking.pdf
- ↑ "Inefficiency in packing squares with unit squares", Journal of Combinatorial Theory, Series A 24 (2): 170–186, 1978, doi:10.1016/0097-3165(78)90005-5
- ↑ Friedman, Erich, Squares in Circles, https://erich-friedman.github.io/packing/squincir/
External links
- Friedman, Erich, Squares in Squares, Erich's Packing Center, https://erich-friedman.github.io/packing/squinsqu/
 |