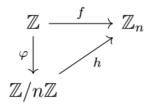Fundamental theorem on homomorphisms
In abstract algebra, the fundamental theorem on homomorphisms, also known as the fundamental homomorphism theorem, or the first isomorphism theorem, relates the structure of two objects between which a homomorphism is given, and of the kernel and image of the homomorphism.
The homomorphism theorem is used to prove the isomorphism theorems.
Group theoretic version
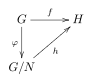
Given two groups G and H and a group homomorphism f : G → H, let N be a normal subgroup in G and φ the natural surjective homomorphism G → G/N (where G/N is the quotient group of G by N). If N is a subset of ker(f) then there exists a unique homomorphism h: G/N → H such that f = h∘φ.
In other words, the natural projection φ is universal among homomorphisms on G that map N to the identity element.
The situation is described by the following commutative diagram:
h is injective if and only if N = ker(f). Therefore, by setting N = ker(f) we immediately get the first isomorphism theorem.
We can write the statement of the fundamental theorem on homomorphisms of groups as "every homomorphic image of a group is isomorphic to a quotient group".
Proof
The proof follows from two basic facts about homomorphisms, namely their preservation of the group operation, and their mapping of the identity element to the identity element. We need to show that if [math]\displaystyle{ \phi: G \to H }[/math] is a homomorphism of groups, then:
1. [math]\displaystyle{ \text{im}(\phi) }[/math] is a subgroup of [math]\displaystyle{ H }[/math].
2. [math]\displaystyle{ G / \ker(\phi) }[/math] is isomorphic to [math]\displaystyle{ \text{im}(\phi) }[/math].
Proof of 1
The operation that is preserved by [math]\displaystyle{ \phi }[/math] is the group operation. If [math]\displaystyle{ a, b \in \text{im}(\phi) }[/math], then there exist elements [math]\displaystyle{ a', b' \in G }[/math] such that [math]\displaystyle{ \phi(a')=a }[/math] and [math]\displaystyle{ \phi(b')=b }[/math]. For these [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math], we have [math]\displaystyle{ ab = \phi(a')\phi(b') = \phi(a'b') \in \text{im}(\phi) }[/math] (since [math]\displaystyle{ \phi }[/math] preserves the group operation), and thus, the closure property is satisfied in [math]\displaystyle{ \text{im}(\phi) }[/math]. The identity element [math]\displaystyle{ e \in H }[/math] is also in [math]\displaystyle{ \text{im}(\phi) }[/math] because [math]\displaystyle{ \phi }[/math] maps the identity element of [math]\displaystyle{ G }[/math] to it. Since every element [math]\displaystyle{ a' }[/math] in [math]\displaystyle{ G }[/math] has an inverse [math]\displaystyle{ (a')^{-1} }[/math]such that [math]\displaystyle{ \phi((a')^{-1}) = (\phi(a'))^{-1} }[/math] (because [math]\displaystyle{ \phi }[/math] preserves the inverse property as well), we have an inverse for each element [math]\displaystyle{ \phi(a') = a }[/math] in [math]\displaystyle{ \text{im}(\phi) }[/math], therefore, [math]\displaystyle{ \text{im}(\phi) }[/math] is a subgroup of [math]\displaystyle{ H }[/math].
Proof of 2
Construct a map [math]\displaystyle{ \psi: G / \ker(\phi) \to \text{im}(\phi) }[/math] by [math]\displaystyle{ \psi(a\ker(\phi)) = \phi(a) }[/math]. This map is well-defined, as if [math]\displaystyle{ a\ker(\phi) = b\ker(\phi) }[/math], then [math]\displaystyle{ b^{-1}a \in \ker(\phi) }[/math] and so [math]\displaystyle{ \phi(b^{-1}a) = e \Rightarrow \phi(b^{-1})\phi(a) = e }[/math] which gives [math]\displaystyle{ \phi(a) = \phi(b) }[/math]. This map is an isomorphism. [math]\displaystyle{ \psi }[/math] is surjective onto [math]\displaystyle{ \text{im}(\phi) }[/math] by definition. To show injectiveness, if [math]\displaystyle{ \psi(a\ker(\phi)) = \psi(b\ker(\phi)) }[/math], then [math]\displaystyle{ \phi(a) = \phi(b) }[/math], which implies [math]\displaystyle{ b^{-1}a \in\ker(\phi) }[/math] so [math]\displaystyle{ a\ker(\phi) = b\ker(\phi) }[/math]. Finally, [math]\displaystyle{ \psi((a\ker(\phi))(b\ker(\phi))) = \psi(ab\ker(\phi)) = \phi(ab) = \phi(a)\phi(b) = \psi(a\ker(\phi))\psi(b\ker(\phi)) }[/math]hence [math]\displaystyle{ \psi }[/math] preserves the group operation. Hence [math]\displaystyle{ \psi }[/math] is an isomorphism between [math]\displaystyle{ G / \ker(\phi) }[/math] and [math]\displaystyle{ \text{im}(\phi) }[/math], which completes the proof.
Applications
The group theoretic version of fundamental homomorphism theorem can be used to show that two selected groups are isomorphic. Two examples are shown below.
The integers modulo n
For each [math]\displaystyle{ n \in \mathbb{N} }[/math], consider the groups [math]\displaystyle{ \mathbb{Z} }[/math] and [math]\displaystyle{ \mathbb{Z}_n }[/math] and a group homomorphism [math]\displaystyle{ f:\mathbb{Z} \rightarrow \mathbb{Z}_n }[/math] defined by [math]\displaystyle{ m \mapsto m \text{ mod }n }[/math] (see modular arithmetic). Next, consider the kernel of [math]\displaystyle{ f }[/math], [math]\displaystyle{ \text{ker} (f) = n \mathbb{Z} }[/math], which is a normal subgroup in [math]\displaystyle{ \mathbb{Z} }[/math]. There exists a natural surjective homomorphism [math]\displaystyle{ \varphi : \mathbb{Z} \rightarrow \mathbb{Z}/n\mathbb{Z} }[/math] defined by [math]\displaystyle{ m \mapsto m+n\mathbb{Z} }[/math]. The theorem asserts that there exists an isomorphism [math]\displaystyle{ h }[/math] between [math]\displaystyle{ \mathbb{Z}_n }[/math] and [math]\displaystyle{ \mathbb{Z}/n\mathbb{Z} }[/math], or in other words [math]\displaystyle{ \mathbb{Z}_n \cong \mathbb{Z}/n \mathbb{Z} }[/math]. The commutative diagram is illustrated below.
N/C Theorem
Let [math]\displaystyle{ G }[/math] be a group with subgroup [math]\displaystyle{ H }[/math]. Let [math]\displaystyle{ C_G(H) }[/math], [math]\displaystyle{ N_G(H) }[/math] and [math]\displaystyle{ \text{Aut}(H) }[/math] be the centralizer, the normalizer and the automorphism group of [math]\displaystyle{ H }[/math] in [math]\displaystyle{ G }[/math], respectively. Then, N/C theorem states that [math]\displaystyle{ N_G(H)/C_G(H) }[/math] is isomorphic to a subgroup of [math]\displaystyle{ \text{Aut}(H) }[/math].
Proof
We are able to find a group homomorphism [math]\displaystyle{ f: N_G(H) \rightarrow \text{Aut}(H) }[/math] defined by [math]\displaystyle{ g \mapsto ghg^{-1} }[/math], for all [math]\displaystyle{ h \in H }[/math]. Clearly, the kernel of [math]\displaystyle{ f }[/math] is [math]\displaystyle{ C_G(H) }[/math]. Hence, we have a natural surjective homomorphism [math]\displaystyle{ \varphi : N_G(H) \rightarrow N_G(H)/C_G(H) }[/math] defined by [math]\displaystyle{ g \mapsto gC(H) }[/math]. The fundamental homomorphism theorem then asserts that there exists an isomorphism between [math]\displaystyle{ N_G(H)/C_G(H) }[/math] and [math]\displaystyle{ \varphi(N_G(H)) }[/math], which is a subgroup of [math]\displaystyle{ \text{Aut}(H) }[/math].
Other versions
Similar theorems are valid for monoids, vector spaces, modules, and rings.
See also
References
- Beachy, John A. (1999), "Theorem 1.2.7 (The fundamental homomorphism theorem)", Introductory Lectures on Rings and Modules, London Mathematical Society Student Texts, 47, Cambridge University Press, p. 27, ISBN 9780521644075, https://books.google.com/books?id=rnNzivBfgOoC&pg=PA27.
- Grove, Larry C. (2012), "Theorem 1.11 (The Fundamental Homomorphism Theorem)", Algebra, Dover Books on Mathematics, Courier Corporation, p. 11, ISBN 9780486142135, https://books.google.com/books?id=C4TByeUh9A4C&pg=PA11.
- Jacobson, Nathan (2012), "Fundamental theorem on homomorphisms of Ω-algebras", Basic Algebra II, Dover Books on Mathematics (2nd ed.), Courier Corporation, p. 62, ISBN 9780486135212, https://books.google.com/books?id=hn75exNZZ-EC&pg=PA62.
- Rose, John S. (1994), "3.24 Fundamental theorem on homomorphisms", A course on Group Theory [reprint of the 1978 original], Dover Publications, Inc., New York, pp. 44–45, ISBN 0-486-68194-7, https://books.google.com/books?id=TWDCAgAAQBAJ&pg=PA44.
 |