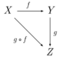2-functor
From HandWiki
In mathematics, specifically, in category theory, a 2-functor is a morphism between 2-categories.[1] They may be defined formally using enrichment by saying that a 2-category is exactly a Cat-enriched category and a 2-functor is a Cat-functor.[2] Explicitly, if C and D are 2-categories then a 2-functor [math]\displaystyle{ F\colon C\to D }[/math] consists of
- a function [math]\displaystyle{ F\colon \text{Ob} C\to \text{Ob} D }[/math], and
- for each pair of objects [math]\displaystyle{ c,c'\in\text{Ob} C }[/math], a functor [math]\displaystyle{ F_{c,c'}\colon \text{Hom}_{C}(c,c')\to\text{Hom}_D(Fc,Fc') }[/math]
such that each [math]\displaystyle{ F_{c,c} }[/math] strictly preserves identity objects and they commute with horizontal composition in C and D.
See [3] for more details and for lax versions.
References
 |