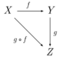2-ring

In mathematics, a categorical ring is, roughly, a category equipped with addition and multiplication. In other words, a categorical ring is obtained by replacing the underlying set of a ring by a category. For example, given a ring R, let C be a category whose objects are the elements of the set R and whose morphisms are only the identity morphisms. Then C is a categorical ring. But the point is that one can also consider the situation in which an element of R comes with a "nontrivial automorphism" (cf. Lurie).

This line of generalization of a ring eventually leads to the notion of an E_n-ring.

See also

• Categorification
• Higher-dimensional algebra

References

• Laplaza, M. Coherence for distributivity. Coherence in categories, 29-65. Lecture Notes in Mathematics 281, Springer-Verlag, 1972.
• Lurie, J. Derived Algebraic Geometry V: Structured Spaces

External links

• http://ncatlab.org/nlab/show/2-rig