Initial and terminal objects

Short description: Special objects used in (mathematical) category theory

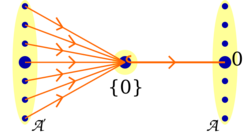
In category theory, a branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X.

The dual notion is that of a terminal object (also called terminal element): T is terminal if for every object X in C there exists exactly one morphism X → T. Initial objects are also called coterminal or universal, and terminal objects are also called final.

If an object is both initial and terminal, it is called a zero object or null object. A pointed category is one with a zero object.

A strict initial object I is one for which every morphism into I is an isomorphism.

Examples

• The empty set is the unique initial object in Set, the category of sets. Every one-element set (singleton) is a terminal object in this category; there are no zero objects. Similarly, the empty space is the unique initial object in Top, the category of topological spaces and every one-point space is a terminal object in this category.
• In the category Rel of sets and relations, the empty set is the unique initial object, the unique terminal object, and hence the unique zero object.

Morphisms of pointed sets. The image also applies to algebraic zero objects

• In the category of pointed sets (whose objects are non-empty sets together with a distinguished element; a morphism from (A, a) to (B, b) being a function f : A → B with f(a) = b), every singleton is a zero object. Similarly, in the category of pointed topological spaces, every singleton is a zero object.
• In Grp, the category of groups, any trivial group is a zero object. The trivial object is also a zero object in Ab, the category of abelian groups, Rng the category of pseudo-rings, R-Mod, the category of modules over a ring, and K-Vect, the category of vector spaces over a field. See Zero object (algebra) for details. This is the origin of the term "zero object".
• In Ring, the category of rings with unity and unity-preserving morphisms, the ring of integers Z is an initial object. The zero ring consisting only of a single element 0 = 1 is a terminal object.
• In Rig, the category of rigs with unity and unity-preserving morphisms, the rig of natural numbers N is an initial object. The zero rig, which is the zero ring, consisting only of a single element 0 = 1 is a terminal object.
• In Field, the category of fields, there are no initial or terminal objects. However, in the subcategory of fields of fixed characteristic, the prime field is an initial object.
• Any partially ordered set (P, ≤) can be interpreted as a category: the objects are the elements of P, and there is a single morphism from x to y if and only if x ≤ y. This category has an initial object if and only if P has a least element; it has a terminal object if and only if P has a greatest element.
• Cat, the category of small categories with functors as morphisms has the empty category, 0 (with no objects and no morphisms), as initial object and the terminal category, 1 (with a single object with a single identity morphism), as terminal object.
• In the category of schemes, Spec(Z), the prime spectrum of the ring of integers, is a terminal object. The empty scheme (equal to the prime spectrum of the zero ring) is an initial object.
• A limit of a diagram F may be characterised as a terminal object in the category of cones to F. Likewise, a colimit of F may be characterised as an initial object in the category of co-cones from F.
• In the category Ch_R of chain complexes over a commutative ring R, the zero complex is a zero object.
• In a short exact sequence of the form 0 → a → b → c → 0, the initial and terminal objects are the anonymous zero object. This is used frequently in cohomology theories.

Properties

Existence and uniqueness

Initial and terminal objects are not required to exist in a given category. However, if they do exist, they are essentially unique. Specifically, if I₁ and I₂ are two different initial objects, then there is a unique isomorphism between them. Moreover, if I is an initial object then any object isomorphic to I is also an initial object. The same is true for terminal objects.

For complete categories there is an existence theorem for initial objects. Specifically, a (locally small) complete category C has an initial object if and only if there exist a set I (not a proper class) and an I-indexed family (K_i) of objects of C such that for any object X of C, there is at least one morphism K_i → X for some i ∈ I.

Equivalent formulations

Terminal objects in a category C may also be defined as limits of the unique empty diagram 0 → C. Since the empty category is vacuously a discrete category, a terminal object can be thought of as an empty product (a product is indeed the limit of the discrete diagram {X_i}, in general). Dually, an initial object is a colimit of the empty diagram 0 → C and can be thought of as an empty coproduct or categorical sum.

It follows that any functor which preserves limits will take terminal objects to terminal objects, and any functor which preserves colimits will take initial objects to initial objects. For example, the initial object in any concrete category with free objects will be the free object generated by the empty set (since the free functor, being left adjoint to the forgetful functor to Set, preserves colimits).

Initial and terminal objects may also be characterized in terms of universal properties and adjoint functors. Let 1 be the discrete category with a single object (denoted by •), and let U : C → 1 be the unique (constant) functor to 1. Then

• An initial object I in C is a universal morphism from • to U. The functor which sends • to I is left adjoint to U.
• A terminal object T in C is a universal morphism from U to •. The functor which sends • to T is right adjoint to U.

Relation to other categorical constructions

Many natural constructions in category theory can be formulated in terms of finding an initial or terminal object in a suitable category.

• A universal morphism from an object X to a functor U can be defined as an initial object in the comma category (X ↓ U). Dually, a universal morphism from U to X is a terminal object in (U ↓ X).
• The limit of a diagram F is a terminal object in Cone(F), the category of cones to F. Dually, a colimit of F is an initial object in the category of cones from F.
• A representation of a functor F to Set is an initial object in the category of elements of F.
• The notion of final functor (respectively, initial functor) is a generalization of the notion of final object (respectively, initial object).

Other properties

• The endomorphism monoid of an initial or terminal object I is trivial: End(I) = Hom(I, I) = { id_I }.
• If a category C has a zero object 0, then for any pair of objects X and Y in C, the unique composition X → 0 → Y is a zero morphism from X to Y.

References

• Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Abstract and Concrete Categories. The joy of cats. John Wiley & Sons. ISBN 0-471-60922-6. http://katmat.math.uni-bremen.de/acc/acc.pdf. Retrieved 2008-01-15. 
• Pedicchio, Maria Cristina; Tholen, Walter, eds (2004). Categorical foundations. Special topics in order, topology, algebra, and sheaf theory. Encyclopedia of Mathematics and Its Applications. 97. Cambridge: Cambridge University Press. ISBN 0-521-83414-7. 
• Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. 5 (2nd ed.). Springer-Verlag. ISBN 0-387-98403-8. 
• This article is based in part on PlanetMath's article on examples of initial and terminal objects.