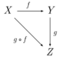Outline of category theory
From HandWiki
Short description: Overview of and topical guide to category theory
The following outline is provided as an overview of and guide to category theory, the area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows (also called morphisms, although this term also has a specific, non category-theoretical sense), where these collections satisfy certain basic conditions. Many significant areas of mathematics can be formalised as categories, and the use of category theory allows many intricate and subtle mathematical results in these fields to be stated, and proved, in a much simpler way than without the use of categories.
Essence of category theory
Branches of category theory
- Homological algebra
- Diagram chasing
- Topos theory
- Enriched category theory
- Higher category theory
- Categorical logic
Specific categories
- Category of sets
- Category of vector spaces
- Category of graded vector spaces
- Category of chain complexes
- Category of finite dimensional Hilbert spaces
- Category of sets and relations
- Category of topological spaces
- Category of metric spaces
- Category of preordered sets
- Category of groups
- Category of abelian groups
- Category of rings
- Category of magmas
- Category of medial magmas
Objects
- Initial object
- Terminal object
- Zero object
- Subobject
- Group object
- Magma object
- Natural number object
- Exponential object
Morphisms
- Epimorphism
- Monomorphism
- Zero morphism
- Normal morphism
- Dual (category theory)
- Groupoid
- Image (category theory)
- Coimage
- Commutative diagram
- Cartesian morphism
- Slice category
Functors
- Isomorphism of categories
- Natural transformation
- Equivalence of categories
- Subcategory
- Faithful functor
- Full functor
- Forgetful functor
- Yoneda lemma
- Representable functor
- Functor category
- Adjoint functors
- Galois connection
- Pontryagin duality
- Affine scheme
- Monad (category theory)
- Comonad
- Combinatorial species
- Exact functor
- Derived functor
- Dominant functor
- Enriched functor
- Kan extension of a functor
- Hom functor
Limits
- Product (category theory)
- Equaliser (mathematics)
- Kernel (category theory)
- Pullback (category theory)/fiber product
- Inverse limit
- Pro-finite group
- Colimit
- Biproduct
Additive structure
- Preadditive category
- Additive category
- Pre-Abelian category
- Abelian category
- Injective cogenerator
- Derived category
- Triangulated category
- Model category
- 2-category
Dagger categories
- Dagger symmetric monoidal category
- Dagger compact category
- Strongly ribbon category
Monoidal categories
- Closed monoidal category
- Braided monoidal category
Cartesian closed category
- Topos
- Category of small categories
Structure
- Semigroupoid
- Comma category
- Localization of a category
- Enriched category
- Bicategory
Topoi, toposes
- Sheaf
- Gluing axiom
- Descent (category theory)
- Grothendieck topology
- Introduction to topos theory
- Subobject classifier
- Pointless topology
- Heyting algebra
History of category theory
Persons influential in the field of category theory
Category theory scholars
- Saunders Mac Lane
- Samuel Eilenberg
- Max Kelly
- William Lawvere
- André Joyal
See also
References
 |