Africa (fractal)

Fractal Africa

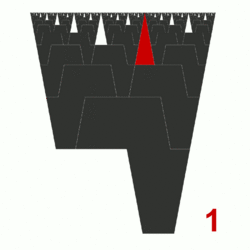
Africa is a fractal made of a set of octagons that have some resemblance to the shape of Africa. The number of octagons of different sizes in the fractal is related to the Fibonacci sequence: 1, 2, 3, 5, 8, 13, 21, .... The height of the largest octagon of the fractal is φ times longer than that of the second octagon; where φ is the golden ratio.

Definition

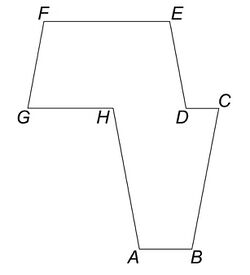
The original version of the fractal was defined by the octagon with the following vertices:

[math]\displaystyle{ A=(a_1,a_2)=\left(0,0\right) }[/math]	[math]\displaystyle{ B=(b_1,b_2)=\left(2,0\right) }[/math]
[math]\displaystyle{ C=(c_1,c_2)=\left(3,\frac{16}{3}\right) }[/math]	[math]\displaystyle{ D=(d_1,d_2)=\left(4-\sqrt{5}, \frac{16}{3}\right) }[/math]
[math]\displaystyle{ E=(e_1,e_2)=\left(\frac{9-3\sqrt{5}}{2},\frac{8\sqrt{5}+8}{3}\right) }[/math]	[math]\displaystyle{ F=(f_1,f_2)=\left(\frac{-3+\sqrt{5}}{2}-\frac{\sqrt{5}-3}{2-\sqrt{5}},\frac{8\sqrt{5}+8}{3}\right) }[/math]
[math]\displaystyle{ G=(g_1,g_2)=\left(-1-\frac{\sqrt{5}-3}{2-\sqrt{5}},\frac{16}{3}\right) }[/math]	[math]\displaystyle{ H=(h_1,h_2)=\left(-1,\frac{16}{3}\right) }[/math]

The following relations are obvious and necessary based on the shape of fractal:

[math]\displaystyle{ c_1-b_1=a_1-h_1 }[/math]

[math]\displaystyle{ d_1-e_1=f_1-g_1 }[/math]

[math]\displaystyle{ c_2-b_2=h_2-a_2 }[/math]

[math]\displaystyle{ e_2-d_2=f_2-g_2 }[/math]

[math]\displaystyle{ \frac{b_1-a_1}{c_1-d_1}=\frac{c_1-b_1}{d_1-e_1}=\frac{c_2-b_2}{e_2-d_2}= \frac{1+\sqrt5}{2}=\varphi }[/math]

[math]\displaystyle{ \frac{2(h_1-g_1)}{\varphi}+\frac{b_1-a_1}{\varphi^2}=e_1-f_1 }[/math]

where φ is the golden ratio. The fractal is made up of a countable number of copies of the octagon and its lateral inversion. The octagon has some resemblance to the shape of Africa:

Tessellation

The shape of the fractal can form the following tessellations:

• 
• 

Properties

In the fractal, the number of octagons of each size (in order of size) is the Fibonacci sequence from the second term: 1, 2, 3, 5, 8, 13, 21, .... The number of isosceles triangles of each size (in order of size) is the Fibonacci sequence from the first term: 1, 1, 2, 3, 5, 8, 13, 21, ....

• 
•