Mandelbulb

Short description: Three-dimensional fractal

File:Visit of the Mandelbulb (4K UHD; 50FPS).webm

A ray-traced image of the 3D Mandelbulb for the iteration v ↦ v⁸ + c

The Mandelbulb is a three-dimensional fractal, constructed for the first time in 1997 by Jules Ruis and in 2009 further developed by Daniel White and Paul Nylander using spherical coordinates.

A canonical 3-dimensional Mandelbrot set does not exist, since there is no 3-dimensional analogue of the 2-dimensional space of complex numbers. It is possible to construct Mandelbrot sets in 4 dimensions using quaternions and bicomplex numbers.

White and Nylander's formula for the "nth power" of the vector [math]\displaystyle{ \mathbf v = \langle x, y, z\rangle }[/math] in ℝ³ is

[math]\displaystyle{ \mathbf v^n := r^n \langle\sin(n\theta) \cos(n\phi), \sin(n\theta) \sin(n\phi), \cos(n\theta)\rangle, }[/math]

where

[math]\displaystyle{ r = \sqrt{x^2 + y^2 + z^2}, }[/math]

[math]\displaystyle{ \phi = \arctan\frac{y}{x} = \arg(x + yi), }[/math]

[math]\displaystyle{ \theta = \arctan\frac{\sqrt{x^2 + y^2}}{z} = \arccos\frac{z}{r}. }[/math]

The Mandelbulb is then defined as the set of those [math]\displaystyle{ \mathbf c }[/math] in ℝ³ for which the orbit of [math]\displaystyle{ \langle 0, 0, 0\rangle }[/math] under the iteration [math]\displaystyle{ \mathbf v \mapsto \mathbf v^n + \mathbf c }[/math] is bounded. For n > 3, the result is a 3-dimensional bulb-like structure with fractal surface detail and a number of "lobes" depending on n. Many of their graphic renderings use n = 8. However, the equations can be simplified into rational polynomials when n is odd. For example, in the case n = 3, the third power can be simplified into the more elegant form:

[math]\displaystyle{ \langle x, y, z\rangle^3 = \left\langle\frac{(3z^2 - x^2 - y^2) x (x^2 - 3y^2)}{x^2 + y^2}, \frac{(3z^2 - x^2 - y^2) y (3x^2 - y^2)}{x^2 + y^2}, z (z^2 - 3x^2 - 3y^2)\right\rangle. }[/math]

The Mandelbulb given by the formula above is actually one in a family of fractals given by parameters (p, q) given by

[math]\displaystyle{ \mathbf v^n := r^n \langle\sin(p\theta) \cos(q\phi), \sin(p\theta) \sin(q\phi), \cos(p\theta)\rangle. }[/math]

Since p and q do not necessarily have to equal n for the identity |vⁿ| = |v|ⁿ to hold, more general fractals can be found by setting

[math]\displaystyle{ \mathbf v^n := r^n \big\langle\sin\big(f(\theta, \phi)\big) \cos\big(g(\theta, \phi)\big), \sin\big(f(\theta, \phi)\big) \sin\big(g(\theta, \phi)\big), \cos\big(f(\theta, \phi)\big)\big\rangle }[/math]

for functions f and g.

Cubic formula

Cubic fractal

Other formulae come from identities parametrising the sum of squares to give a power of the sum of squares, such as

[math]\displaystyle{ (x^3 - 3xy^2 - 3xz^2)^2 + (y^3 - 3yx^2 + yz^2)^2 + (z^3 - 3zx^2 + zy^2)^2 = (x^2 + y^2 + z^2)^3, }[/math]

which we can think of as a way to cube a triplet of numbers so that the modulus is cubed. So this gives, for example,

[math]\displaystyle{ x \to x^3 - 3x (y^2 + z^2) + x_0 }[/math]

[math]\displaystyle{ y \to -y^3 + 3 y x^2 - y z^2 + y_0 }[/math]

[math]\displaystyle{ z \to z^3 - 3 z x^2 + z y^2 + z_0 }[/math]

or other permutations.

This reduces to the complex fractal [math]\displaystyle{ w \to w^3 + w_0 }[/math] when z = 0 and [math]\displaystyle{ w \to \overline{w}^3 + w_0 }[/math] when y = 0.

There are several ways to combine two such "cubic" transforms to get a power-9 transform, which has slightly more structure.

Quintic formula

Quintic Mandelbulb

Quintic Mandelbulb with C = 2

Another way to create Mandelbulbs with cubic symmetry is by taking the complex iteration formula [math]\displaystyle{ z \to z^{4m+1} + z_0 }[/math] for some integer m and adding terms to make it symmetrical in 3 dimensions but keeping the cross-sections to be the same 2-dimensional fractal. (The 4 comes from the fact that [math]\displaystyle{ i^4 = 1 }[/math].) For example, take the case of [math]\displaystyle{ z \to z^5 + z_0 }[/math]. In two dimensions, where [math]\displaystyle{ z = x + iy }[/math], this is

[math]\displaystyle{ x \to x^5 - 10 x^3 y^2 + 5 x y^4 + x_0, }[/math]

[math]\displaystyle{ y \to y^5 - 10 y^3 x^2 + 5 y x^4 + y_0. }[/math]

This can be then extended to three dimensions to give

[math]\displaystyle{ x \to x^5 - 10 x^3 (y^2 + A y z + z^2) + 5 x (y^4 + B y^3 z + C y^2 z^2 + B y z^3 + z^4) + D x^2 y z (y+z) + x_0, }[/math]

[math]\displaystyle{ y \to y^5 - 10 y^3 (z^2 + A x z + x^2) + 5 y (z^4 + B z^3 x + C z^2 x^2 + B z x^3 + x^4) + D y^2 z x (z+x)+ y_0, }[/math]

[math]\displaystyle{ z \to z^5 - 10 z^3 (x^2 + A x y + y^2) + 5 z (x^4 + B x^3 y + C x^2 y^2 + B x y^3 + y^4) + D z^2 x y (x+y) +z_0 }[/math]

for arbitrary constants A, B, C and D, which give different Mandelbulbs (usually set to 0). The case [math]\displaystyle{ z \to z^9 }[/math] gives a Mandelbulb most similar to the first example, where n = 9. A more pleasing result for the fifth power is obtained by basing it on the formula [math]\displaystyle{ z \to -z^5 + z_0 }[/math].

Fractal based on z → −z⁵

Power-nine formula

Fractal with z⁹ Mandelbrot cross-sections

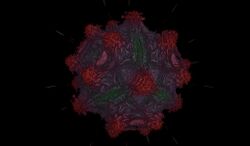
This fractal has cross-sections of the power-9 Mandelbrot fractal. It has 32 small bulbs sprouting from the main sphere. It is defined by, for example,

[math]\displaystyle{ x \to x^9 - 36 x^7 (y^2 + z^2) + 126 x^5 (y^2 + z^2)^2 - 84 x^3 (y^2 + z^2)^3 + 9 x (y^2 + z^2)^4 + x_0, }[/math]

[math]\displaystyle{ y \to y^9 - 36 y^7 (z^2 + x^2) + 126 y^5 (z^2 + x^2)^2 - 84 y^3 (z^2 + x^2)^3 + 9 y (z^2 + x^2)^4 + y_0, }[/math]

[math]\displaystyle{ z \to z^9 - 36 z^7 (x^2 + y^2) + 126 z^5 (x^2 + y^2)^2 - 84 z^3 (x^2 + y^2)^3 + 9 z (x^2 + y^2)^4 + z_0. }[/math]

These formula can be written in a shorter way:

[math]\displaystyle{ x \to \frac{1}{2} \left(x + i\sqrt{y^2 + z^2}\right)^9 + \frac{1}{2} \left(x - i\sqrt{y^2 + z^2}\right)^9 + x_0 }[/math]

and equivalently for the other coordinates.

Power-nine fractal detail

Spherical formula

A perfect spherical formula can be defined as a formula

[math]\displaystyle{ (x,y,z) \to \big(f(x, y, z) + x_0, g(x, y, z) + y_0, h(x, y, z) + z_0\big), }[/math]

where

[math]\displaystyle{ (x^2 + y^2 + z^2)^n = f(x, y, z)^2 + g(x, y, z)^2 + h(x, y, z)^2, }[/math]

where f, g and h are nth-power rational trinomials and n is an integer. The cubic fractal above is an example.

Uses in media

• In the 2014 computer-animated film Big Hero 6, the climax takes place in the middle of a wormhole, which is represented by the stylized interior of a Mandelbulb.
• In the 2018 science fiction horror film Annihilation, an extraterrestrial being appears in the form of a partial Mandelbulb.
• In the webcomic Unsounded the spirit realm of the khert is represented by a stylized golden mandelbulb.

See also

• Mandelbox
• List of fractals by Hausdorff dimension

References

6. http://www.fractal.org the Fractal Navigator by Jules Ruis

External links

• for the first use of the Mandelbulb formula on www.fractal.org website Jules Ruis
• Mandelbulb: The Unravelling of the Real 3D Mandelbrot Fractal, on Daniel White's website
• Several variants of the Mandelbulb, on Paul Nylander's website
• An opensource fractal renderer that can be used to create images of the Mandelbulb
• Formula for Mandelbulb/Juliabulb/Juliusbulb by Jules Ruis
• Mandelbulb/Juliabulb/Juliusbulb with examples of real 3D objects
• Video : View of the Mandelbulb
• Video : Exploring Mandelbulb. 3D Fractal Animation
• The discussion thread in Fractalforums.com that led to the Mandelbulb
• Video fly through of an animated Mandelbulb world
• Open-source Mandelbulber v2 software - Explore trigonometric, hyper-complex, Mandelbox, IFS, and many other 3D fractals.