Angular aperture

The angular aperture of a thin lens with focal point at F and an aperture of diameter [math]\displaystyle{ D }[/math].

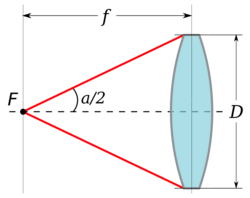
The angular aperture of a lens is the angular size of the lens aperture as seen from the focal point:

[math]\displaystyle{ a = 2 \arctan \left( \frac {D/2} {f} \right) = 2 \arctan \left( \frac {D} {2f} \right) }[/math]

where

[math]\displaystyle{ f }[/math] is the focal length

[math]\displaystyle{ D }[/math] is the diameter of the aperture.

Relation to numerical aperture

In a medium with an index of refraction close to 1, such as air, the angular aperture is approximately equal to twice the numerical aperture of the lens.

Formally, the numerical aperture in air is:

[math]\displaystyle{ \mathrm{NA} = \sin a/2 = \sin \arctan \left( \frac {D} {2 f} \right) }[/math]

In the paraxial approximation, with a small aperture, [math]\displaystyle{ D\lt f }[/math]:

[math]\displaystyle{ \mathrm{NA} \approx a/2 }[/math]

See also

• f-number
• Numerical aperture
• Acceptance angle, half the angular aperture
• Field of view