Astronomy:Mars cycler

From HandWiki
Short description: Kind of spacecraft trajectory
A Mars cycler is an elliptical orbit (green) that crosses the orbits of Earth (blue) and Mars (red), and encounters both planets at the points where it crosses their orbits, although not necessarily on every orbit. (Not to scale.)

A Mars cycler (or Earth–Mars cycler) is a kind of spacecraft trajectory that encounters Earth and Mars regularly. The term Mars cycler may also refer to a spacecraft on a Mars cycler trajectory. The Aldrin cycler is an example of a Mars cycler.

Cyclers are potentially useful for transporting people or materials between those bodies using minimal propellant (relying on gravity-assist flybys for most trajectory changes) and can carry heavy radiation shielding to protect people in transit from cosmic rays and solar storms.

Earth–Mars cyclers

A cycler is a trajectory that encounters two or more bodies regularly. Once the orbit is established, no propulsion is required to shuttle between the two, although some minor corrections may be necessary due to small perturbations in the orbit. The use of cyclers was considered in 1969 by Walter M. Hollister, who examined the case of an Earth–Venus cycler.[1] Hollister did not have any particular mission in mind, but posited their use for both regular communication between two planets, and for multi-planet flyby missions.[2]

A Martian year is 1.8808 Earth years, so Mars makes eight orbits of the Sun in about the same time as Earth makes 15. Cycler trajectories between Earth and Mars occur in whole-number multiples of the synodic period between the two planets, which is about 2.135 Earth years.[3] In 1985, Buzz Aldrin presented an extension of his earlier Lunar cycler work which identified a Mars cycler corresponding to a single synodic period.[4] The Aldrin cycler (as it is now known) makes a single eccentric loop around the Sun. It travels from Earth to Mars in 146 days (4.8 months), spends the next 16 months beyond the orbit of Mars, and takes another 146 days going from the orbit of Mars back to the first crossing of Earth's orbit.[5]

The existence of the now-eponymous Aldrin cycler was calculated and confirmed by scientists at Jet Propulsion Laboratory later that year, along with the VISIT-1 and VISIT-2 cyclers proposed by John Niehoff in 1985.[6] [7] For each Earth–Mars cycler that is not a multiple of seven synodic periods, an outbound cycler intersects Mars on the way out from Earth while an inbound cycler intersects Mars on the way in to Earth. The only difference in these trajectories is the date in the synodic period in which the vehicle is launched from Earth. Earth–Mars cyclers with a multiple of seven synodic periods return to Earth at nearly the same point in its orbit and may encounter Earth and/or Mars multiple times during each cycle. VISIT-1 encounters Earth three times and Mars four times in 15 years. VISIT-2 encounters Earth five times and Mars two times in 15 years.[5] Some possible Earth–Mars cyclers include the following:[5]

Synodic periods per cycle Solar revolutions per cycle Time per cycle (years) Aphelion radius (AU) Earth/Mars transfer time (days) Notes
1 1 2.135 2.23 146 Aldrin cycler
2 2 4.27 2.33 158
2 3 4.27 1.51 280 Aphelion inside semi-major axis of Mars orbit
3 4 6.405 1.89 189
3 5 6.405 1.45 274 Aphelion inside semi-major axis of Mars orbit
3 5 6.405 1.52 134 Aphelion inside semi-major axis of Mars orbit
4 5 8.54 1.82 88
4 6 8.54 1.53 157 Aphelion inside aphelion of Mars orbit
5 4 10.675 2.49 75
5 5 10.675 2.09 89
5 6 10.675 1.79 111
5 7 10.675 1.54 170 Aphelion inside aphelion of Mars orbit
5 8 10.675 1.34 167 Aphelion inside semi-major axis of Mars orbit
6 4 12.81 2.81 87
6 5 12.81 2.37 97
6 6 12.81 2.04 111
6 7 12.81 1.78 133 Requires minimal ballistic correction
6 8 12.81 1.57 179 Requires minimal ballistic correction
6 9 12.81 1.40 203 Aphelion inside semi-major axis of Mars orbit; Requires minimal ballistic correction

A detailed survey of Earth–Mars cycler trajectories was conducted by Ryan Russell and Cesar Ocampo from the University of Texas at Austin, Texas . They identified 24 Earth-Mars cyclers with periods of two to four synodic periods, and 92 cyclers with periods of five or six synodic periods. They also found hundreds of non-ballistic cyclers, ones which would require some powered maneuvers.[8]

Physics

Gravity assist velocity diagram.

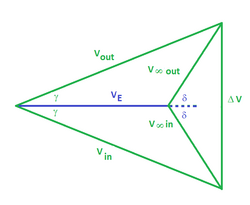
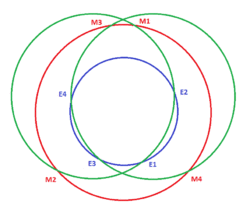
Earth orbits the Sun in one Earth year, Mars in 1.881. Neither orbit is perfectly circular; Earth has an orbital eccentricity of 0.0168, and Mars of 0.0934. The two orbits are not quite coplanar either, as the orbit of Mars is inclined by 1.85 degrees to that of Earth. The effect of the gravity of Mars on the cycler orbits is almost negligible, but that of the far more massive Earth needs to be considered. If we ignore these factors, and approximate Mars's orbital period as 1.875 Earth years, then 15 Earth years is 8 Martian years. In the diagram opposite, a spacecraft in an Aldrin cycler orbit that starts from Earth at point E1 will encounter Mars at M1. When it gets back to E1 just over two Earth years later, Earth will no longer be there, but it will encounter Earth again at E2, which is [math]\displaystyle{ 51.4^\circ }[/math], ​1⁄7 of an Earth orbit, further round.[9]

The shape of the cycler orbit can be obtained from the conic equation:

[math]\displaystyle{ r = a\frac{1-\epsilon^2}{1+\epsilon\cos\theta} }[/math]

Where [math]\displaystyle{ r }[/math] is 1 astronomical unit, [math]\displaystyle{ a }[/math] is the semi-major axis, [math]\displaystyle{ \epsilon }[/math] is the orbital eccentricity and [math]\displaystyle{ \theta=-25.7^\circ }[/math] (half of [math]\displaystyle{ -51.4^\circ }[/math]). We can obtain [math]\displaystyle{ a }[/math] by solving Lambert's problem with [math]\displaystyle{ 51.4^\circ }[/math] as the initial and final transfer angle. This gives:

[math]\displaystyle{ a = 1.60 }[/math]

Solving the quadratic equation gives:

[math]\displaystyle{ \epsilon = 0.393 }[/math]

with an orbital period of 2.02 years.[9]

The angle at which the spacecraft flies past Earth, [math]\displaystyle{ \gamma }[/math], is given by:

[math]\displaystyle{ \tan \gamma = \frac{\epsilon r\sin\theta}{a(1-\epsilon^2)} }[/math]

Substituting the values given and derived above gives a value for [math]\displaystyle{ \gamma }[/math] of [math]\displaystyle{ 7.18^\circ }[/math]. We can calculate the gravity assist from Earth:

[math]\displaystyle{ \Delta V = 2 V \sin \gamma }[/math]

where [math]\displaystyle{ V }[/math] is the heliocentric flyby velocity. This can be calculated from:

[math]\displaystyle{ V = V_E\sqrt{2-\frac{r}{a}} }[/math]

where V E  is the velocity of Earth, which is 29.8 km/s. Substituting gives us V = 34.9 km/s, and Template:DELTAV = 8.73 km/s.[9]

The excess speed is given by:

[math]\displaystyle{ V_\infty = \sqrt{V^2 + V_E^2 -2 V V_E \cos \gamma} }[/math]

Which gives a value for V ∞  of 6.54 km/s. The turn angle [math]\displaystyle{ \delta }[/math] can be calculated from:

[math]\displaystyle{ \Delta V = 2 V_\infty \sin \delta }[/math]

Which gives [math]\displaystyle{ \delta = 41.9^\circ }[/math], meaning that we have an [math]\displaystyle{ 83.8^\circ }[/math] turn. The radius of closest approach to Earth r p  will be given by:

[math]\displaystyle{ \sin \delta = \frac{1}{1+\frac{r_pV_\infty^2}{\mu_E}} }[/math]

Where μ E  is the gravitational constant of the Earth. Substituting the values gives r p  = 4,640 kilometres (2,880 mi), which is bad because the radius of the Earth is 6,371 kilometres (3,959 mi). A correction would therefore be required to comfortably avoid the planet.[9]

Proposed use

Rather than wait for the cycler to come around again, Aldrin proposed using a second cycler to make the return trip. (Not to scale.)

Aldrin proposed a pair of Mars cycler vehicles providing regular transport between Earth and Mars.[4] While astronauts can tolerate traveling to the Moon in relatively cramped spacecraft for a few days, a mission to Mars, lasting several months, would require much more habitable accommodations for the much longer journey: astronauts would need a facility with ample living space, life support, and heavy radiation shielding.[6][10] A 1999 NASA study estimated that a mission to Mars would require lifting about 437 metric tons (482 short tons) into space, of which 250 metric tons (280 short tons) was propellant.[11]

Aldrin proposed that the costs of Mars missions could be greatly reduced by use of large space stations in cyclic orbits called castles. Once established in their orbits, they would make regular trips between Earth and Mars without requiring any propellant. Other than consumables, cargo would therefore only have to be launched once.[6][10] Two castles would be used, an outbound one on an Aldrin cycler with a fast transfer to Mars and long trip back, and an inbound one with fast trip to Earth and long return to Mars,[3] which Aldrin called up and down escalators.[6]

The astronauts would meet up with the cycler in Earth orbit and later Mars orbit in specialised craft called taxis. One cycler would travel an outbound route from Earth to Mars in about five months. Another Mars cycler in a complementary trajectory would travel from Mars to Earth, also in about five months. Taxi and cargo vehicles[lower-alpha 1] would attach to the cycler at one planet and detach upon reaching the other.[11] The cycler concept would therefore provide for routine, safe, and economical transport between Earth and Mars.[12]

A significant drawback of the cycler concept was that the Aldrin cycler flies by both planets at high speed. A taxi would need to accelerate to 15,000 miles per hour (6.7 km/s) around Earth, and 22,000 miles per hour (9.8 km/s) near Mars. To get around this, Aldrin proposed what he called a semi-cycler, in which the castle would slow down around Mars, orbiting it, and later resume the cycler orbit. This would require fuel to execute the braking and re-cycling maneuvers.[10][11]

The castles could be inserted into cycler orbits with considerable savings in fuel by performing a series of low thrust maneuvers:[12] The castle would be placed into an interim orbit upon launch, and then use an Earth-swing-by maneuver to boost it into the final cycler orbit.[13] Assuming the use of conventional fuels,[lower-alpha 2] it is possible to estimate the fuel required to establish a cycler orbit.[14] In the case of the Aldrin cycler, use of a gravity assist reduces the fuel requirement by about 24.3 metric tons (26.8 short tons), or 15 percent. Other cyclers showed less impressive improvement, due to the shape of their orbits, and when they encounter the Earth. In the case of the VISIT-1 cycler, the benefit would be around 0.2 metric tons (0.22 short tons), less than one percent, which would hardly justify the additional three years required to establish the orbit.[14]

See also

Notes

  1. ↑ Most cargo would be sent directly to Mars, as the advantages of a cycler (living space, shielding, and life support systems) are of value primarily to human passengers.
  2. ↑ Conventional propellants in the vicinity of Earth are liquid hydrogen and liquid oxygen, which can be refrigerated on the ground and used during or soon after launch. The 2×H2 + O2 combination has a specific impulse of about 450 s (4.4 km/s). Deep space maneuvers use toxic, non-cryogenic mono-methyl hydrazine and nitrogen tetroxide propellants (e.g. used by the Galileo spacecraft) with a 300 s (2.9 km/s) specific impulse. Safer and more efficient cryogenic fuels like O2 and H2 cannot be economically carried into deep space: without prohibitively massive refrigeration they boil away.

References

  1. ↑ Hollister 1969, p. 366.
  2. ↑ Hollister 1969, p. 369.
  3. ↑ 3.0 3.1 Byrnes, Longuski & Aldrin 1993, p. 334.
  4. ↑ 4.0 4.1 Aldrin 1985, pp. 3–10.
  5. ↑ 5.0 5.1 5.2 McConaghy, Longuski & Byrnes 2002, p. 6.
  6. ↑ 6.0 6.1 6.2 6.3 Friedlander et al. 1986, p. 31.
  7. ↑ McConaghy, Longuski & Byrnes 2002, p. 1.
  8. ↑ Russell & Ocampo 2004, p. 321.
  9. ↑ 9.0 9.1 9.2 9.3 Byrnes, Longuski & Aldrin 1993, pp. 334–335.
  10. ↑ 10.0 10.1 10.2 Aldrin, Buzz; Noland, David (13 December 2005). "Buzz Aldrin's roadmap to Mars – A PM exclusive". Popular Mechanics. http://www.popularmechanics.com/space/moon-mars/a333/2076326/. 
  11. ↑ 11.0 11.1 11.2 Bellows, Alan (10 April 2008). "The Martian Express". http://www.damninteresting.com/?p=960. 
  12. ↑ 12.0 12.1 Rogers et al. 2015, p. 114.
  13. ↑ Rogers et al. 2015, pp. 120–121.
  14. ↑ 14.0 14.1 Rogers et al. 2015, p. 123.

Additional references



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Mars_cycler&oldid=3350590"