Astronomy:Stellar pulsation

From HandWiki
Light curve of a Delta Cephei variable, showing the regular light curve formed by intrinsic stellar pulsations

Stellar pulsations are caused by expansions and contractions in the outer layers as a star seeks to maintain equilibrium. These fluctuations in stellar radius cause corresponding changes in the luminosity of the star. Astronomers are able to deduce this mechanism by measuring the spectrum and observing the Doppler effect.[1] Many intrinsic variable stars that pulsate with large amplitudes, such as the classical Cepheids, RR Lyrae stars and large-amplitude Delta Scuti stars show regular light curves.

This regular behavior is in contrast with the variability of stars that lie parallel to and to the high-luminosity/low-temperature side of the classical variable stars in the Hertzsprung–Russell diagram. These giant stars are observed to undergo pulsations ranging from weak irregularity, when one can still define an average cycling time or period, (as in most RV Tauri and semiregular variables) to the near absence of repetitiveness in the irregular variables. The W Virginis variables are at the interface; the short period ones are regular and the longer period ones show first relatively regular alternations in the pulsations cycles, followed by the onset of mild irregularity as in the RV Tauri stars into which they gradually morph as their periods get longer.[2][3] Stellar evolution and pulsation theories suggest that these irregular stars have a much higher luminosity to mass (L/M) ratios.

Many stars are non-radial pulsators, which have smaller fluctuations in brightness than those of regular variables used as standard candles.[4][5]

Regular variables

A prerequisite for irregular variability is that the star be able to change its amplitude on the time scale of a period. In other words, the coupling between pulsation and heat flow must be sufficiently large to allow such changes. This coupling is measured by the relative linear growth- or decay rate κ (kappa) of the amplitude of a given normal mode in one pulsation cycle (period). For the regular variables (Cepheids, RR Lyrae, etc.) numerical stellar modeling and linear stability analysis show that κ is at most of the order of a couple of percent for the relevant, excited pulsation modes. On the other hand, the same type of analysis shows that for the high L/M models κ is considerably larger (30% or higher).

For the regular variables the small relative growth rates κ imply that there are two distinct time scales, namely the period of oscillation and the longer time associated with the amplitude variation. Mathematically speaking, the dynamics has a center manifold, or more precisely a near center manifold. In addition, it has been found that the stellar pulsations are only weakly nonlinear in the sense that their description can be limited powers of the pulsation amplitudes. These two properties are very general and occur for oscillatory systems in many other fields such as population dynamics, oceanography, plasma physics, etc.

The weak nonlinearity and the long time scale of the amplitude variation allows the temporal description of the pulsating system to be simplified to that of only the pulsation amplitudes, thus eliminating motion on the short time scale of the period. The result is a description of the system in terms of amplitude equations that are truncated to low powers of the amplitudes. Such amplitude equations have been derived by a variety of techniques, e.g. the Poincaré–Lindstedt method of elimination of secular terms, or the multi-time asymptotic perturbation method,[6][7][8] and more generally, normal form theory.[9][10][11]

For example, in the case of two non-resonant modes, a situation generally encountered in RR Lyrae variables, the temporal evolution of the amplitudes A1 and A2 of the two normal modes 1 and 2 is governed by the following set of ordinary differential equations [math]\displaystyle{ \begin{align} \frac{dA_1}{dt} &= \kappa_1 A_1 + \left(Q_{11} A_1^2 + Q_{12} A_2^2\right) A_1 \\[1ex] \frac{dA_2}{dt} &= \kappa_2 A_2 + \left(Q_{21} A_1^2 + Q_{22} A_2^2\right) A_2 \end{align} }[/math] where the Qij are the nonresonant coupling coefficients.[12][13]

These amplitude equations have been limited to the lowest order nontrivial nonlinearities. The solutions of interest in stellar pulsation theory are the asymptotic solutions (as time tends towards infinity) because the time scale for the amplitude variations is generally very short compared to the evolution time scale of the star which is the nuclear burning time scale. The equations above have fixed point solutions with constant amplitudes, corresponding to single-mode (A1[math]\displaystyle{ \neq }[/math] 0, A2 = 0) or (A1 = 0, A2[math]\displaystyle{ \neq }[/math] 0) and double-mode (A1[math]\displaystyle{ \neq }[/math] 0, A2[math]\displaystyle{ \neq }[/math]0) solutions. These correspond to singly periodic and doubly periodic pulsations of the star. It is important to emphasize that no other asymptotic solution of the above equations exists for physical (i.e., negative) coupling coefficients.

For resonant modes the appropriate amplitude equations have additional terms that describe the resonant coupling among the modes. The Hertzsprung progression in the light curve morphology of classical (singly periodic) Cepheids is the result of a well-known 2:1 resonance among the fundamental pulsation mode and the second overtone mode.[14] The amplitude equation can be further extended to nonradial stellar pulsations.[15][16]

In the overall analysis of pulsating stars, the amplitude equations allow the bifurcation diagram between possible pulsational states to be mapped out. In this picture, the boundaries of the instability strip where pulsation sets in during the star's evolution correspond to a Hopf bifurcation.[17]

The existence of a center manifold eliminates the possibility of chaotic (i.e. irregular) pulsations on the time scale of the period. Although resonant amplitude equations are sufficiently complex to also allow for chaotic solutions, this is a very different chaos because it is in the temporal variation of the amplitudes and occurs on a long time scale.

While long term irregular behavior in the temporal variations of the pulsation amplitudes is possible when amplitude equations apply, this is not the general situation. Indeed, for the majority of the observations and modeling, the pulsations of these stars occur with constant Fourier amplitudes, leading to regular pulsations that can be periodic or multi-periodic (quasi-periodic in the mathematical literature).

Irregular pulsations

The light curves of intrinsic variable stars with large amplitudes have been known for centuries to exhibit behavior that goes from extreme regularity, as for the classical Cepheids and the RR Lyrae stars, to extreme irregularity, as for the so-called Irregular variables. In the Population II stars this irregularity gradually increases from the low period W Virginis variables through the RV Tauri variables into the regime of the semiregular variables. Low-dimensional chaos in stellar pulsations is the current interpretation of this established phenomenon.

Regular behavior of the Cepheids

The regular behavior of the Cepheids has been successfully modeled with numerical hydrodynamics since the 1960s,[18][19] and from a theoretical point of view it is easily understood as due to the presence of center manifold which arises because of the weakly dissipative nature of the dynamical system.[20] This, and the fact that the pulsations are weakly nonlinear, allows a description of the system in terms of amplitude equations[21] [22] and a construction of the bifurcation diagram (see also bifurcation theory) of the possible types of pulsation (or limit cycles), such fundamental mode pulsation, first or second overtone pulsation, or more complicated, double-mode pulsations in which several modes are excited with constant amplitudes. The boundaries of the instability strip where pulsation sets in during the star's evolution correspond to a Hopf bifurcation.

Irregularity of Population II stars

In contrast, the irregularity of the large amplitude Population II stars is more challenging to explain. The variation of the pulsation amplitude over one period implies large dissipation, and therefore there exists no center manifold. Various mechanisms have been proposed, but are found lacking. One, suggests the presence of several closely spaced pulsation frequencies that would beat against each other, but no such frequencies exist in the appropriate stellar models. Another, more interesting suggestion is that the variations are of a stochastic nature,[23] but no mechanism has been proposed or exists that could provide the energy for such large observed amplitude variations. It is now established that the mechanism behind the irregular light curves is an underlying low dimensional chaotic dynamics (see also Chaos theory). This conclusion is based on two types of studies.

CFD simulations

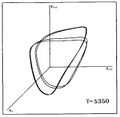
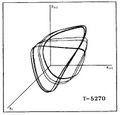
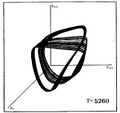
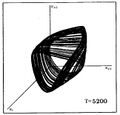
The computational fluid dynamics numerical forecasts for the pulsations of sequences of W Virginis stellar models exhibit two approaches to irregular behavior that are a clear signature of low dimensional chaos. The first indication comes from first return maps in which one plots one maximum radius, or any other suitable variable, versus the next one. The sequence of models shows a period doubling bifurcation, or cascade, leading to chaos. The near quadratic shape of the map is indicative of chaos and implies an underlying horseshoe map.[24][25] Other sequences of models follow a somewhat different route, but also to chaos, namely the Pommeau–Manneville or tangent bifurcation route.[26][27]

The following shows a similar visualization of the period doubling cascade to chaos for a sequence of stellar models that differ by their average surface temperature T. The graph shows triplets of values of the stellar radius (Ri, Ri+1, Ri+2) where the indices i, i+1, i+2 indicate successive time intervals.

PeriodiDoubling1.jpg PeriodDoubling2.jpg Period Doubling3.jpg PeriodDoubling4.jpg PeriodDoubling5.jpg PeriodDoubling6.jpg
P0 P2 P4 P8 Banded Chaos FullChaos

The presence of low dimensional chaos is also confirmed by another, more sophisticated, analysis of the model pulsations which extracts the lowest unstable periodic orbits and examines their topological organization (twisting). The underlying attractor is found to be banded like the Roessler attractor, with however an additional twist in the band.[28]

Global flow reconstruction from observed light curves

The method of global flow reconstruction[29] uses a single observed signal {si} to infer properties of the dynamical system that generated it. First N-dimensional 'vectors' [math]\displaystyle{ S_i=s_i,s_{i-1},s_{i-2},...s_{i-N+1} }[/math] are constructed. The next step consists in finding an expression for the nonlinear evolution operator [math]\displaystyle{ M }[/math] that takes the system from time [math]\displaystyle{ i }[/math] to time [math]\displaystyle{ i+1 }[/math], i.e., [math]\displaystyle{ S_{i+1}=M(S_i) }[/math]. Takens' theorem guarantees that under very general circumstances the topological properties of this reconstructed evolution operator are the same as that of the physical system, provided the embedding dimension N is large enough. Thus from the knowledge of a single observed variable one can infer properties about the real physical system which is governed by a number of independent variables.

This approach has been applied to the AAVSO data for the star R Scuti[30][31] It could be inferred that the irregular pulsations of this star arise from an underlying 4-dimensional dynamics. Phrased differently this says that from any 4 neighboring observations one can predict the next one. From a physical point of view it says that there are 4 independent variables that describe the dynamic of the system. The method of false nearest neighbors corroborates an embedding dimension of 4. The fractal dimension of the dynamics of R Scuti as inferred from the computed Lyapunov exponents lies between 3.1 and 3.2.

Top: R Scuti observed AAVSO light curve (smoothed); Bottom: Synthetic light curve, obtained with the help of the reconstructed evolution operator. Note the similarity with the observed light curve.

From an analysis of the fixed points of the evolution operator a nice physical picture can be inferred, namely that the pulsations arise from the excitation of an unstable pulsation mode that couples nonlinearly to a second, stable pulsation mode which is in a 2:1 resonance with the first one, a scenario described by the Shilnikov theorem.[32]

This resonance mechanism is not limited to R Scuti, but has been found to hold for several other stars for which the observational data are sufficiently good.[33]

See also

References

  1. ↑ Koupelis, Theo (2010). In Quest of the Universe. Jones and Bartlett Titles in Physical Science (6th ed.). Jones & Bartlett Learning. ISBN 978-0-7637-6858-4. https://books.google.com/books?id=GVlpKZ67DscC&pg=PA401. 
  2. ↑ Alcock, C.; Allsman, R. A.; Alves, D. R.; Axelrod, T. S.; Becker, A.; Bennett, D. P.; Cook, K. H.; Freeman, K. C. et al. (1998). "The MACHO Project LMC Variable Star Inventory. VII. The Discovery of RV Tauri Stars and New Type II Cepheids in the Large Magellanic Cloud". The Astronomical Journal 115 (5): 1921. doi:10.1086/300317. Bibcode: 1998AJ....115.1921A. 
  3. ↑ Soszyński, I.; Udalski, A.; Szymański, M. K.; Kubiak, M.; Pietrzyński, G.; Wyrzykowski, Ł.; Szewczyk, O.; Ulaczyk, K. et al. (2008). "The Optical Gravitational Lensing Experiment. The OGLE-III Catalog of Variable Stars. II.Type II Cepheids and Anomalous Cepheids in the Large Magellanic Cloud". Acta Astronomica 58: 293. Bibcode: 2008AcA....58..293S. 
  4. ↑ Grigahcène, A.; Antoci, V.; Balona, L.; Catanzaro, G.; Daszyńska-Daszkiewicz, J.; Guzik, J. A.; Handler, G.; Houdek, G. et al. (2010). "Hybrid γ Doradus-δ Scuti Pulsators: New Insights into the Physics of the Oscillations from Kepler Observations". The Astrophysical Journal 713 (2): L192. doi:10.1088/2041-8205/713/2/L192. Bibcode: 2010ApJ...713L.192G. 
  5. ↑ Mosser, B.; Belkacem, K.; Goupil, M. -J.; Miglio, A.; Morel, T.; Barban, C.; Baudin, F.; Hekker, S. et al. (2010). "Red-giant seismic properties analyzed with CoRoT". Astronomy and Astrophysics 517: A22. doi:10.1051/0004-6361/201014036. Bibcode: 2010A&A...517A..22M. 
  6. ↑ Dziembowski, W. (1980). "Delta Scuti variables - the link between giant- and dwarf-type pulsators". Nonradial and Nonlinear Stellar Pulsation. Lecture Notes in Physics 125: 22–33. doi:10.1007/3-540-09994-8_2. ISBN 978-3-540-09994-9. Bibcode: 1980LNP...125...22D. 
  7. ↑ Buchler, J. R.; Goupil, M. -J. (1984). "Amplitude equations for nonadiabatic nonlinear stellar pulsators. I - the formalism". The Astrophysical Journal 279: 394. doi:10.1086/161900. Bibcode: 1984ApJ...279..394B. 
  8. ↑ Buchler, J. R. (1993). "A Dynamical Systems Approach to Nonlinear Stellar Pulsations". Astrophysics and Space Science 210 (1–2): 9–31. doi:10.1007/BF00657870. Bibcode: 1993Ap&SS.210....9B. 
  9. ↑ Guckenheimer, John; Holmes, Philip; Slemrod, M. (1984). "Nonlinear Oscillations Dynamical Systems, and Bifurcations of Vector Fields". Journal of Applied Mechanics 51 (4): 947. doi:10.1115/1.3167759. Bibcode: 1984JAM....51..947G. 
  10. ↑ Coullet, P. H.; Spiegel, E. A. (1983). "Amplitude Equations for Systems with Competing Instabilities". SIAM Journal on Applied Mathematics 43 (4): 776–821. doi:10.1137/0143052. 
  11. ↑ Spiegel, E. A. (1985). "Cosmic Arrhythmias". Chaos in Astrophysics. pp. 91–135. doi:10.1007/978-94-009-5468-7_3. ISBN 978-94-010-8914-2. 
  12. ↑ Buchler, J. Robert; Kovacs, Geza (1987). "Modal Selection in Stellar Pulsators. II. Application to RR Lyrae Models". The Astrophysical Journal 318: 232. doi:10.1086/165363. Bibcode: 1987ApJ...318..232B. 
  13. ↑ Van Hoolst, T. (1996). "Effects of nonlinearities on a single oscillation mode of a star". Astronomy and Astrophysics 308: 66. Bibcode: 1996A&A...308...66V. 
  14. ↑ Buchler, J. Robert; Moskalik, Pawel; Kovacs, Geza (1990). "A Survey of Bump Cepheid Model Pulsations". The Astrophysical Journal 351: 617. doi:10.1086/168500. Bibcode: 1990ApJ...351..617B. 
  15. ↑ Van Hoolst, Tim (1994). "Coupled-mode equations and amplitude equations for nonadiabatic, nonradial oscillations of stars". Astronomy and Astrophysics 292: 471. Bibcode: 1994A&A...292..471V. 
  16. ↑ Buchler, J. R.; Goupil, M. -J.; Hansen, C. J. (1997). "On the role of resonances in nonradial pulsators". Astronomy and Astrophysics 321: 159. Bibcode: 1997A&A...321..159B. 
  17. ↑ Kolláth, Z.; Buchler, J. R.; Szabó, R.; Csubry, Z.; Morel, T.; Barban, C.; Baudin, F.; Hekker, S. et al. (2002). "Nonlinear beat Cepheid and RR Lyrae models". Astronomy and Astrophysics 385 (3): 932–939. doi:10.1051/0004-6361:20020182. Bibcode: 2002A&A...385..932K. 
  18. ↑ Christy, Robert F. (1964). "The Calculation of Stellar Pulsation". Reviews of Modern Physics 36 (2): 555–571. doi:10.1103/RevModPhys.36.555. Bibcode: 1964RvMP...36..555C. https://authors.library.caltech.edu/33166/1/CHRrmp64.pdf. 
  19. ↑ Cox, Arthur N.; Brownlee, Robert R.; Eilers, Donald D. (1966). "Time-Dependent Method for Computation of Radiation Diffusion and Hydro-Dynamics". The Astrophysical Journal 144: 1024. doi:10.1086/148701. Bibcode: 1966ApJ...144.1024C. 
  20. ↑ Buchler, J. R. (1993). "A Dynamical Systems Approach to Nonlinear Stellar Pulsations". Astrophysics and Space Science 210 (1–2): 9–31. doi:10.1007/BF00657870. Bibcode: 1993Ap&SS.210....9B. 
  21. ↑ Spiegel, E. A. (1985). "Cosmic Arrhythmias". Chaos in Astrophysics. pp. 91–135. doi:10.1007/978-94-009-5468-7_3. ISBN 978-94-010-8914-2. 
  22. ↑ Klapp, J.; Goupil, M. J.; Buchler, J. R. (1985). "Amplitude equations for nonadiabatic nonlinear stellar pulsators. II - Application to realistic resonant Cepheid models". The Astrophysical Journal 296: 514. doi:10.1086/163471. Bibcode: 1985ApJ...296..514K. 
  23. ↑ Konig, M.; Paunzen, E.; Timmer, J. (1999). "On the irregular temporal behaviour of the variable star R Scuti". Monthly Notices of the Royal Astronomical Society 303 (2): 297. doi:10.1046/j.1365-8711.1999.02216.x. Bibcode: 1999MNRAS.303..297K. 
  24. ↑ Aikawa, Toshiki (1990). "Intermittent Chaos in a Subharmonic Bifurcation Sequence of Stellar Pulsation Models". Astrophysics and Space Science 164 (2): 295–307. doi:10.1007/BF00658831. Bibcode: 1990Ap&SS.164..295A. 
  25. ↑ Kovacs, Geza; Buchler, J. Robert (1988). "Regular and Irregular Nonlinear Pulsations in Population II Cepheid Models". The Astrophysical Journal 334: 971. doi:10.1086/166890. Bibcode: 1988ApJ...334..971K. .
  26. ↑ Buchler, J.R., Goupil M.J. & Kovacs G. 1987, Tangent Bifurcations and Intermittency in the Pulsations of Population II Cepheid Models, Physics Letters A 126, 177–180.
  27. ↑ Aikawa, Toshiki (1987). "The Pomeau-Manneville Intermittent Transition to Chaos in Hydrodynamic Pulsation Models". Astrophysics and Space Science 139 (2): 281–293. doi:10.1007/BF00644357. Bibcode: 1987Ap&SS.139..281A. 
  28. ↑ Letellier, C.; Gouesbet, G.; Soufi, F.; Buchler, J. R.; Kolláth, Z. (1996). "Chaos in variable stars: Topological analysis of W Vir model pulsations". Chaos 6 (3): 466–476. doi:10.1063/1.166189. PMID 12780277. Bibcode: 1996Chaos...6..466L. https://hal.archives-ouvertes.fr/hal-01596864/file/LetellierChaos1996.pdf. 
  29. ↑ Packard, N. H.; Crutchfield, J. P.; Farmer, J. D.; Shaw, R. S. (1980). "Geometry from a time series". Physical Review Letters 45 (9): 712. doi:10.1103/PhysRevLett.45.712. Bibcode: 1980PhRvL..45..712P. 
  30. ↑ Buchler, J. Robert; Serre, Thierry; Kolláth, Zoltán; Mattei, Janet (1995). "A choatic pulsating star: The case of R Scuti". Physical Review Letters 74 (6): 842–845. doi:10.1103/PhysRevLett.74.842. PMID 10058863. Bibcode: 1995PhRvL..74..842B. 
  31. ↑ Packard, N. H.; Crutchfield, J. P.; Farmer, J. D.; Shaw, R. S. (1980). "Geometry from a time series". Physical Review Letters 45 (9): 712. doi:10.1103/PhysRevLett.45.712. Bibcode: 1980PhRvL..45..712P. 
  32. ↑ Leonov, G. A. (2013). "Shilnikov Chaos in Lorenz-Like Systems". International Journal of Bifurcation and Chaos 23 (3): 1350058. doi:10.1142/S0218127413500582. Bibcode: 2013IJBC...2350058L. 
  33. ↑ Buchler, J. Robert; Kolláth, Zoltán; Cadmus, Robert R. (2004). "Evidence for Low-dimensional Chaos in Semiregular Variable Stars". The Astrophysical Journal 613 (1): 532–547. doi:10.1086/422903. Bibcode: 2004ApJ...613..532B. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Stellar_pulsation&oldid=3347431"