Astronomy:Solar-like oscillations
Solar-like oscillations are oscillations in stars that are excited in the same way as those in the Sun, namely by turbulent convection in its outer layers. Stars that show solar-like oscillations are called solar-like oscillators. The oscillations are standing pressure and mixed pressure-gravity modes that are excited over a range in frequency, with the amplitudes roughly following a bell-shaped distribution. Unlike opacity-driven oscillators, all the modes in the frequency range are excited, making the oscillations relatively easy to identify. The surface convection also damps the modes, and each is well-approximated in frequency space by a Lorentzian curve, the width of which corresponds to the lifetime of the mode: the faster it decays, the broader is the Lorentzian. All stars with surface convection zones are expected to show solar-like oscillations, including cool main-sequence stars (up to surface temperatures of about 7000K), subgiants and red giants. Because of the small amplitudes of the oscillations, their study has advanced tremendously thanks to space-based missions[1] (mainly COROT and Kepler).
Solar-like oscillations have been used, among other things, to precisely determine the masses and radii of planet-hosting stars and thus improve the measurements of the planets' masses and radii.[2][3]
Red giants
In red giants, mixed modes are observed, which are in part directly sensitive to the core properties of the star. These have been used to distinguish red giants burning helium in their cores from those that are still only burning hydrogen in a shell,[4] to show that the cores of red giants are rotating more slowly than models predict[5] and to constrain the internal magnetic fields of the cores[6]
Echelle diagrams
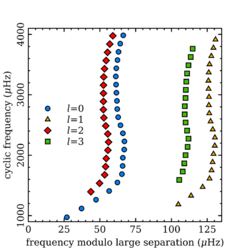
The peak of the oscillation power roughly corresponds to lower frequencies and radial orders for larger stars. For the Sun, the highest amplitude modes occur around a frequency of 3 mHz with order , and no mixed modes are observed. For more massive and more evolved stars, the modes are of lower radial order and overall lower frequencies. Mixed modes can be seen in the evolved stars. In principle, such mixed modes may also be present in main-sequence stars but they are at too low frequency to be excited to observable amplitudes. High-order pressure modes of a given angular degree are expected to be roughly evenly-spaced in frequency, with a characteristic spacing known as the large separation .[9] This motivates the echelle diagram, in which the mode frequencies are plotted as a function of the frequency modulo the large separation, and modes of a particular angular degree form roughly vertical ridges.
Scaling relations
The frequency of maximum oscillation power is accepted[10] to vary roughly with the acoustic cut-off frequency, above which waves can propagate in the stellar atmosphere, and thus are not trapped and do not contribute to standing modes. This gives
Similarly, the large frequency separation is known to be roughly proportional to the square root of the density:
When combined with an estimate of the effective temperature, this allows one to solve directly for the mass and radius of the star, basing the constants of proportionality on the known values for the Sun. These are known as the scaling relations:
Equivalently, if one knows the star's luminosity, then the temperature can be replaced via the blackbody luminosity relationship , which gives
Some bright solar-like oscillators
- Procyon
- Alpha Centauri A and B
- Mu Herculis
See also
References
- ↑ Chaplin, W. J.; Miglio, A. (2013). "Asteroseismology of Solar-Type and Red-Giant Stars". Annual Review of Astronomy and Astrophysics 51 (1): 353–392. doi:10.1146/annurev-astro-082812-140938. Bibcode: 2013ARA&A..51..353C.
- ↑ Davies, G. R. et al. (2016). "Oscillation frequencies for 35 Kepler solar-type planet-hosting stars using Bayesian techniques and machine learning". Monthly Notices of the Royal Astronomical Society 456 (2): 2183–2195. doi:10.1093/mnras/stv2593. Bibcode: 2016MNRAS.456.2183D.
- ↑ Silva Aguirre, V. et al. (2015). "Ages and fundamental properties of Kepler exoplanet host stars from asteroseismology". Monthly Notices of the Royal Astronomical Society 452 (2): 2127–2148. doi:10.1093/mnras/stv1388. Bibcode: 2015MNRAS.452.2127S.
- ↑ Bedding, Timothy R. et al. (2011). "Gravity modes as a way to distinguish between hydrogen- and helium-burning red giant stars". Nature 471 (7340): 608–11. doi:10.1038/nature09935. PMID 21455175. Bibcode: 2011Natur.471..608B.
- ↑ Beck, Paul G. et al. (2012). "Fast core rotation in red-giant stars as revealed by gravity-dominated mixed modes". Nature 481 (7379): 55–7. doi:10.1038/nature10612. PMID 22158105. Bibcode: 2012Natur.481...55B.
- ↑ Fuller, J.; Cantiello, M.; Stello, D.; Garcia, R. A.; Bildsten, L. (2015). "Asteroseismology can reveal strong internal magnetic fields in red giant stars". Science 350 (6259): 423–426. doi:10.1126/science.aac6933. PMID 26494754. Bibcode: 2015Sci...350..423F.
- ↑ Broomhall, A.-M. et al. (2009). "Definitive Sun-as-a-star p-mode frequencies: 23 years of BiSON observations". Monthly Notices of the Royal Astronomical Society 396 (1): L100–L104. doi:10.1111/j.1745-3933.2009.00672.x. Bibcode: 2009MNRAS.396L.100B.
- ↑ Davies, G. R.; Chaplin, W. J.; Elsworth, Y.; Hale, S. J. (2014). "BiSON data preparation: a correction for differential extinction and the weighted averaging of contemporaneous data". Monthly Notices of the Royal Astronomical Society 441 (4): 3009–3017. doi:10.1093/mnras/stu803. Bibcode: 2014MNRAS.441.3009D.
- ↑ Tassoul, M. (1980). "Asymptotic approximations for stellar nonradial pulsations". The Astrophysical Journal Supplement Series 43: 469. doi:10.1086/190678. Bibcode: 1980ApJS...43..469T.
- ↑ Kjeldsen, H.; Bedding, T. R. (1995). "Amplitudes of stellar oscillations: the implications for asteroseismology". Astronomy and Astrophysics 293: 87. Bibcode: 1995A&A...293...87K.
External links
- Lecture Notes on Stellar Oscillations published by J. Christensen-Dalsgaard (Aarhus University, Denmark)
 |
