Bounded function

Short description: A mathematical function the set of whose values are bounded

A schematic illustration of a bounded function (red) and an unbounded one (blue). Intuitively, the graph of a bounded function stays within a horizontal band, while the graph of an unbounded function does not.

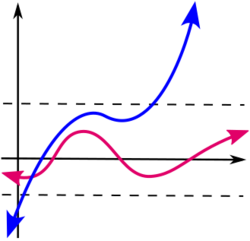
In mathematics, a function $f$ defined on some set $X$ with real or complex values is called bounded if the set of its values is bounded. In other words, there exists a real number $M$ such that

$|f(x)|\le M$

for all $x$ in $X$. A function that is not bounded is said to be unbounded.

If $f$ is real-valued and $f(x)\le A$ for all $x$ in $X$, then the function is said to be bounded (from) above by $A$. If $f(x)\ge B$ for all $x$ in $X$, then the function is said to be bounded (from) below by $B$. A real-valued function is bounded if and only if it is bounded from above and below.

An important special case is a bounded sequence, where $X$ is taken to be the set $\mathbb{\mathbb{N}}$ of natural numbers. Thus a sequence $f=(a_0,a_1,a_2,\dots )$ is bounded if there exists a real number $M$ such that

$|a_n|\le M$

for every natural number $n$. The set of all bounded sequences forms the sequence space $l^{\mathrm{\infty }}$.

The definition of boundedness can be generalized to functions $f:X\to Y$ taking values in a more general space $Y$ by requiring that the image $f(X)$ is a bounded set in $Y$.

Related notions

Weaker than boundedness is local boundedness. A family of bounded functions may be uniformly bounded.

A bounded operator $T:X\to Y$ is not a bounded function in the sense of this page's definition (unless $T=0$), but has the weaker property of preserving boundedness; bounded sets $M\subseteq X$ are mapped to bounded sets $T(M)\subseteq Y$. This definition can be extended to any function $f:X\to Y$ if $X$ and $Y$ allow for the concept of a bounded set. Boundedness can also be determined by looking at a graph.

Examples

• The sine function $\sin :\mathbb{ℝ}\to \mathbb{ℝ}$ is bounded since $|\sin (x)|\le 1$ for all $x\in \mathbb{ℝ}$.
• The function $f(x)=(x^2-1{)}^{-1}$, defined for all real $x$ except for −1 and 1, is unbounded. As $x$ approaches −1 or 1, the values of this function get larger in magnitude. This function can be made bounded if one restricts its domain to be, for example, $[2,\mathrm{\infty })$ or $(-\mathrm{\infty },-2]$.
• The function $f(x)=(x^2+1{)}^{-1}$, defined for all real $x$, is bounded, since $|f(x)|\le 1$ for all $x$.
• The inverse trigonometric function arctangent defined as: $y=\arctan (x)$ or $x=\tan (y)$ is increasing for all real numbers $x$ and bounded with $-\frac{\pi }{2}<y<\frac{\pi }{2}$ radians
• By the boundedness theorem, every continuous function on a closed interval, such as $f:[0,1]\to \mathbb{ℝ}$, is bounded. More generally, any continuous function from a compact space into a metric space is bounded.
• All complex-valued functions $f:\mathbb{ℂ}\to \mathbb{ℂ}$ which are entire are either unbounded or constant as a consequence of Liouville's theorem. In particular, the complex $\sin :\mathbb{ℂ}\to \mathbb{ℂ}$ must be unbounded since it is entire.
• The function $f$ which takes the value 0 for $x$ rational number and 1 for $x$ irrational number (cf. Dirichlet function) is bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on $[0,1]$ is much larger than the set of continuous functions on that interval. Moreover, continuous functions need not be bounded; for example, the functions $g:{\mathbb{ℝ}}^2\to \mathbb{ℝ}$ and $h:(0,1{)}^2\to \mathbb{ℝ}$ defined by $g(x,y):=x+y$ and $h(x,y):=\frac{1}{x+y}$ are both continuous, but neither is bounded. (However, a continuous function must be bounded if its domain is both closed and bounded.)

See also

• Bounded set
• Compact support
• Local boundedness
• Uniform boundedness