Buchdahl's theorem

Short description: Theorem in general relativity

Evolution of central pressure against compactness (radius over mass) for a uniform density 'star'. This central pressure diverges at the Buchdahl bound.

In general relativity, Buchdahl's theorem, named after Hans Adolf Buchdahl, makes more precise the notion that there is a maximal sustainable density for ordinary gravitating matter. It gives an inequality between the mass and radius that must be satisfied for static, spherically symmetric matter configurations under certain conditions. In particular, for areal radius [math]\displaystyle{ R }[/math], the mass [math]\displaystyle{ M }[/math] must satisfy

[math]\displaystyle{ M \lt \frac{4 R c^2}{9G} }[/math]

where [math]\displaystyle{ G }[/math] is the gravitational constant and [math]\displaystyle{ c }[/math] is the speed of light. This inequality is often referred to as Buchdahl's bound. The bound has historically also been called Schwarzschild's limit as it was first noted by Karl Schwarzschild to exist in the special case of a constant density fluid. However, this terminology should not be confused with the Schwarzschild radius which is notably smaller than the radius at the Buchdahl bound.

Theorem

Given a static, spherically symmetric solution to the Einstein equations (without cosmological constant) with matter confined to areal radius [math]\displaystyle{ R }[/math] that behaves as a perfect fluid with a density that does not increase outwards. (An areal radius [math]\displaystyle{ R }[/math] corresponds to a sphere of surface area [math]\displaystyle{ 4 \pi R^2 }[/math]. In curved spacetime the proper radius of such a sphere is not necessarily [math]\displaystyle{ R }[/math].) Assumes in addition that the density and pressure cannot be negative. The mass of this solution must satisfy

[math]\displaystyle{ M \lt \frac{4 R c^2}{9G} }[/math]

For his proof of the theorem, Buchdahl uses the Tolman-Oppenheimer-Volkoff (TOV) equation.

Significance

The Buchdahl theorem is useful when looking for alternatives to black holes. Such attempts are often inspired by the information paradox; a way to explain (part of) the dark matter; or to criticize that observations of black holes are based on excluding known astrophysical alternatives (such as neutron stars) rather than direct evidence. However, to provide a viable alternative it is sometimes needed that the object should be extremely compact and in particular violate the Buchdahl inequality. This implies that one of the assumptions of Buchdahl's theorem must be invalid. A classification scheme can be made based on which assumptions are violated.

Special Cases

Incompressible fluid

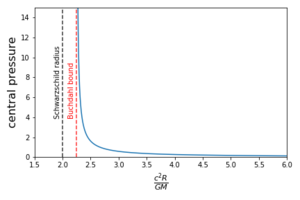
The special case of the incompressible fluid or constant density, [math]\displaystyle{ \rho(r) = \rho_* }[/math] for [math]\displaystyle{ r \lt R }[/math], is a historically important example as, in 1916, Schwarzschild noted for the first time that the mass could not exceed the value [math]\displaystyle{ \frac{4 R c^2}{9G} }[/math] for a given radius [math]\displaystyle{ R }[/math] or the central pressure would become infinite. It is also a particularly tractable example. Within the star one finds.

[math]\displaystyle{ m(r) = \frac{4}{3} \pi r^3 \rho_* }[/math]

and using the TOV-equation

[math]\displaystyle{ p(r) = \rho_* c^2 \frac{R \sqrt{R-2GM/c^2}-\sqrt{R^3-2GMr^2/c^2}}{\sqrt{R^3-2GMr^2/c^2}-3R\sqrt{R-2GM/c^2}} }[/math]

such that the central pressure, [math]\displaystyle{ p(0) }[/math], diverges as [math]\displaystyle{ R \to 9GM/4c^2 }[/math].

Extensions

Extensions to Buchdahl's theorem generally either relax assumptions on the matter or on the symmetry of the problem. For instance, by introducing anisotropic matter or rotation. In addition one can also consider analogues of Buchdahl's theorem in other theories of gravity