Cantellation (geometry)

Short description: Geometric operation on a regular polytope

A cantellated cube - Red faces are reduced. Edges are bevelled, forming new yellow square faces. Vertices are truncated, forming new blue triangle faces.

A cantellated cubic honeycomb - Purple cubes are cantellated. Edges are bevelled, forming new blue cubic cells. Vertices are truncated, forming new red rectified cube cells.

In geometry, a cantellation is a 2nd-order truncation in any dimension that bevels a regular polytope at its edges and at its vertices, creating a new facet in place of each edge and of each vertex. Cantellation also applies to regular tilings and honeycombs. Cantellating a polyhedron is also rectifying its rectification.

Cantellation (for polyhedra and tilings) is also called expansion by Alicia Boole Stott: it corresponds to moving the faces of the regular form away from the center, and filling in a new face in the gap for each opened edge and for each opened vertex.

Notation

A cantellated polytope is represented by an extended Schläfli symbol t_0,2{p,q,...} or r[math]\displaystyle{ \begin{Bmatrix}p\\q\\...\end{Bmatrix} }[/math] or rr{p,q,...}.

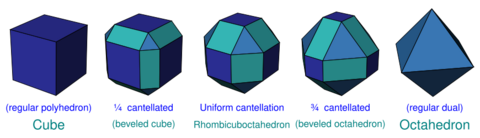
For polyhedra, a cantellation offers a direct sequence from a regular polyhedron to its dual.

Example: cantellation sequence between cube and octahedron:

Example: a cuboctahedron is a cantellated tetrahedron.

For higher-dimensional polytopes, a cantellation offers a direct sequence from a regular polytope to its birectified form.

Examples: cantellating polyhedra, tilings

Regular polyhedra, regular tilings

Form	Polyhedra			Tilings
Coxeter	rTT	rCO	rID	rQQ	rHΔ
Conway notation	eT	eC = eO	eI = eD	eQ	eH = eΔ
Polyhedra to be expanded	Tetrahedron	Cube or octahedron	Icosahedron or dodecahedron	Square tiling	Hexagonal tiling Triangular tiling
Image
Animation

Uniform polyhedra or their duals

Coxeter	rrt{2,3}	rrs{2,6}	rrCO	rrID
Conway notation	eP3	eA4	eaO = eaC	eaI = eaD
Polyhedra to be expanded	Triangular prism or triangular bipyramid	Square antiprism or tetragonal trapezohedron	Cuboctahedron or rhombic dodecahedron	Icosidodecahedron or rhombic triacontahedron
Image
Animation

See also

• Uniform polyhedron
• Uniform 4-polytope
• Chamfer (geometry)

References

• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN:0-486-61480-8 (pp.145-154 Chapter 8: Truncation, p 210 Expansion)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

• Weisstein, Eric W.. "Expansion". http://mathworld.wolfram.com/Expansion.html.