Chamfer (geometry)

Short description: Geometric operation which truncates the edges of polyhedra

Unchamfered, slightly chamfered and chamfered cube

Historical crystal models of slightly chamfered Platonic solids

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.

In Conway polyhedron notation it is represented by the letter c. A polyhedron with e edges will have a chamfered form containing 2e new vertices, 3e new edges, and e new hexagonal faces.

Chamfered Platonic solids

In the chapters below the chamfers of the five Platonic solids are described in detail. Each is shown in a version with edges of equal length and in a canonical version where all edges touch the same midsphere. (They only look noticeably different for solids containing triangles.) The shown duals are dual to the canonical versions.

Seed	150px {3,3}	{4,3}	{3,4}	{5,3}	{3,5}
Chamfered

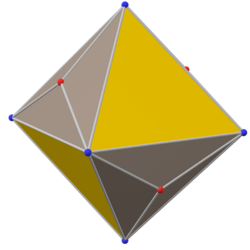
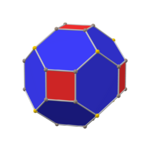
Chamfered tetrahedron

Chamfered tetrahedron
(with equal edge length)
Conway notation	cT
Goldberg polyhedron	GPIII(2,0) = {3+,3}2,0
Faces	4 triangles 6 hexagons
Edges	24 (2 types)
Vertices	16 (2 types)
Vertex configuration	(12) 3.6.6 (4) 6.6.6
Symmetry group	Tetrahedral (Td)
Dual polyhedron	Alternate-triakis tetratetrahedron
Properties	convex, equilateral-faced
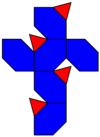net

The chamfered tetrahedron (or alternate truncated cube) is a convex polyhedron constructed as an alternately truncated cube or chamfer operation on a tetrahedron, replacing its 6 edges with hexagons.

It is the Goldberg polyhedron G_III(2,0), containing triangular and hexagonal faces.

The truncated tetrahedron looks similar, but its hexagons correspond to the 4 faces of the original tetrahedron, rather than to its 6 edges.

Tetrahedral chamfers and related solids

chamfered tetrahedron (canonical)	dual of the tetratetrahedron	chamfered tetrahedron (canonical)
alternate-triakis tetratetrahedron	tetratetrahedron	alternate-triakis tetratetrahedron

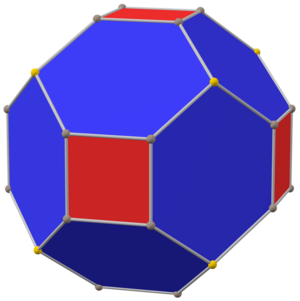
Chamfered cube

Chamfered cube
(with equal edge length)
Conway notation	cC = t4daC
Goldberg polyhedron	GPIV(2,0) = {4+,3}2,0
Faces	6 squares 12 hexagons
Edges	48 (2 types)
Vertices	32 (2 types)
Vertex configuration	(24) 4.6.6 (8) 6.6.6
Symmetry	Oh, [4,3], (*432) Th, [4,3+], (3*2)
Dual polyhedron	Tetrakis cuboctahedron
Properties	convex, equilateral-faced
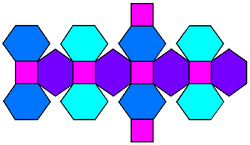net

The chamfered cube is a convex polyhedron with 32 vertices, 48 edges, and 18 faces: 12 hexagons and 6 squares. It is constructed as a chamfer of a cube. The squares are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the tetrakis cuboctahedron.

It is also inaccurately called a truncated rhombic dodecahedron, although that name rather suggests a rhombicuboctahedron. It can more accurately be called a tetratruncated rhombic dodecahedron because only the order-4 vertices are truncated.

The hexagonal faces are equilateral but not regular. They are formed by a truncated rhombus, have 2 internal angles of about 109.47°, or [math]\displaystyle{ \cos^{-1}(-\frac{1}{3}) }[/math], and 4 internal angles of about 125.26°, while a regular hexagon would have all 120° angles.

Because all its faces have an even number of sides with 180° rotation symmetry, it is a zonohedron. It is also the Goldberg polyhedron GP_IV(2,0) or {4+,3}_2,0, containing square and hexagonal faces.

The chamfered cube is the Minkowski sum of a rhombic dodecahedron and a cube of side length 1 when eight vertices of the rhombic dodecahedron are at [math]\displaystyle{ (\pm 1, \pm 1, \pm 1) }[/math] and its six vertices are at the permutations of [math]\displaystyle{ (\pm \sqrt 3, 0, 0) }[/math].

A topological equivalent with pyritohedral symmetry and rectangular faces can be constructed by chamfering the axial edges of a pyritohedron. This occurs in pyrite crystals.

Pyritohedron and its axis truncation

Historical crystallographic models

The truncated octahedron looks similar, but its hexagons correspond to the 8 vertices of the cube, rather than to its 12 edges.

Octahedral chamfers and related solids

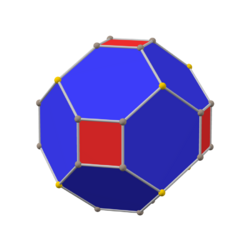chamfered cube (canonical)	rhombic dodecahedron	chamfered octahedron (canonical)
tetrakis cuboctahedron	cuboctahedron	triakis cuboctahedron

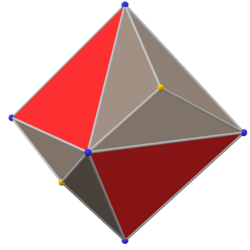
Chamfered octahedron

Chamfered octahedron
(with equal edge length)
Conway notation	cO = t3daO
Faces	8 triangles 12 hexagons
Edges	48 (2 types)
Vertices	30 (2 types)
Vertex configuration	(24) 3.6.6 (6) 6.6.6
Symmetry	Oh, [4,3], (*432)
Dual polyhedron	Triakis cuboctahedron
Properties	convex

In geometry, the chamfered octahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 8 (order 3) vertices.

It can also be called a tritruncated rhombic dodecahedron, a truncation of the order-3 vertices of the rhombic dodecahedron.

The 8 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become triangles.

The hexagonal faces are equilateral but not regular.

Historical drawings of rhombic cuboctahedron and chamfered octahedron

Historical models of triakis cuboctahedron and chamfered octahedron

Chamfered dodecahedron

Chamfered dodecahedron
(with equal edge length)
Conway notation	cD] = t5daD = dk5aD
Goldberg polyhedron	GV(2,0) = {5+,3}2,0
Fullerene	C80
Faces	12 pentagons 30 hexagons
Edges	120 (2 types)
Vertices	80 (2 types)
Vertex configuration	(60) 5.6.6 (20) 6.6.6
Symmetry group	Icosahedral (Ih)
Dual polyhedron	Pentakis icosidodecahedron
Properties	convex, equilateral-faced

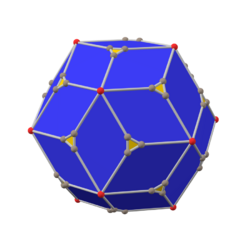
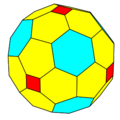
The chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.

It is also inaccurately called a truncated rhombic triacontahedron, although that name rather suggests a rhombicosidodecahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.

The truncated icosahedron looks similar, but its hexagons correspond to the 20 vertices of the dodecahedron, rather than to its 30 edges.

Icosahedral chamfers and related solids

chamfered dodecahedron (canonical)	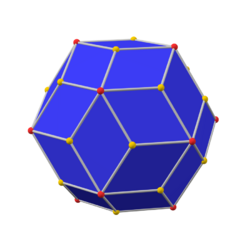rhombic triacontahedron	chamfered icosahedron (canonical)
pentakis icosidodecahedron	icosidodecahedron	triakis icosidodecahedron

Chamfered icosahedron

Chamfered icosahedron
(with equal edge length)
Conway notation	cI = t3daI
Faces	20 triangles 30 hexagons
Edges	120 (2 types)
Vertices	72 (2 types)
Vertex configuration	(24) 3.6.6 (12) 6.6.6
Symmetry	Ih, [5,3], (*532)
Dual polyhedron	triakis icosidodecahedron
Properties	convex

In geometry, the chamfered icosahedron is a convex polyhedron constructed from the rhombic triacontahedron by truncating the 20 order-3 vertices. The hexagonal faces can be made equilateral but not regular.

It can also be called a tritruncated rhombic triacontahedron, a truncation of the order-3 vertices of the rhombic triacontahedron.

Chamfered regular tilings

Chamfered regular and quasiregular tilings

Square tiling, Q {4,4}	Triangular tiling, Δ {3,6}	Hexagonal tiling, H {6,3}	Rhombille, daH dr{6,3}
cQ	cΔ	cH	cdaH

Relation to Goldberg polyhedra

The chamfer operation applied in series creates progressively larger polyhedra with new hexagonal faces replacing edges from the previous one. The chamfer operator transforms GP(m,n) to GP(2m,2n).

A regular polyhedron, GP(1,0), create a Goldberg polyhedra sequence: GP(1,0), GP(2,0), GP(4,0), GP(8,0), GP(16,0)...

	GP(1,0)	GP(2,0)	GP(4,0)	GP(8,0)	GP(16,0)...
GPIV {4+,3}	C	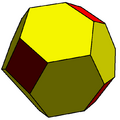cC	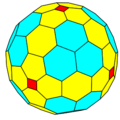ccC	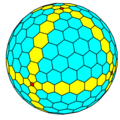cccC
GPV {5+,3}	D	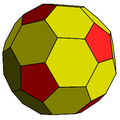cD	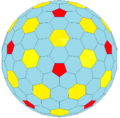ccD	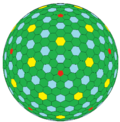cccD	ccccD
GPVI {6+,3}	H	cH	ccH	cccH	ccccH

The truncated octahedron or truncated icosahedron, GP(1,1) creates a Goldberg sequence: GP(1,1), GP(2,2), GP(4,4), GP(8,8)....

	GP(1,1)	GP(2,2)	GP(4,4)...
GPIV {4+,3}	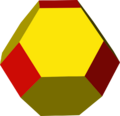tO	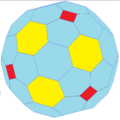ctO	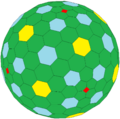cctO
GPV {5+,3}	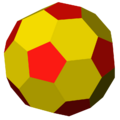tI	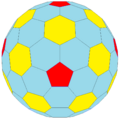ctI	cctI
GPVI {6+,3}	tH	ctH	cctH

A truncated tetrakis hexahedron or pentakis dodecahedron, GP(3,0), creates a Goldberg sequence: GP(3,0), GP(6,0), GP(12,0)...

	GP(3,0)	GP(6,0)	GP(12,0)...
GPIV {4+,3}	tkC	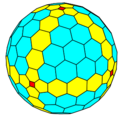ctkC	cctkC
GPV {5+,3}	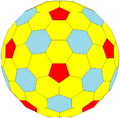tkD	ctkD	cctkD
GPVI {6+,3}	tkH	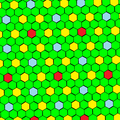ctkH	cctkH

Chamfered polytopes and honeycombs

Like the expansion operation, chamfer can be applied to any dimension. For polygons, it triples the number of vertices. For polychora, new cells are created around the original edges. The cells are prisms, containing two copies of the original face, with pyramids augmented onto the prism sides.

See also

• Conway polyhedron notation
• Near-miss Johnson solid
• Cantellation (geometry)

References

• Goldberg, Michael (1937). "A class of multi-symmetric polyhedra". Tohoku Mathematical Journal 43: 104–108. https://www.jstage.jst.go.jp/article/tmj1911/43/0/43_0_104/_article. 
• Joseph D. Clinton, Clinton’s Equal Central Angle Conjecture [1]
• Hart, George (2012). "Goldberg Polyhedra". in Senechal, Marjorie. Shaping Space (2nd ed.). Springer. pp. 125–138. doi:10.1007/978-0-387-92714-5_9. ISBN 978-0-387-92713-8. https://archive.org/details/shapingspaceexpl00sene. 
• Hart, George (June 18, 2013). "Mathematical Impressions: Goldberg Polyhedra". Simons Science News. https://www.simonsfoundation.org/multimedia/mathematical-impressions-goldberg-polyhedra/. 
• Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullerenes and coordination polyhedra versus half-cube embeddings, 1998 PDF [2] (p. 72 Fig. 26. Chamfered tetrahedron)
• Deza, A.; Deza, M.; Grishukhin, V. (1998), "Fullerenes and coordination polyhedra versus half-cube embeddings", Discrete Mathematics 192 (1): 41–80, doi:10.1016/S0012-365X(98)00065-X .

External links

• Chamfered Tetrahedron
• Chamfered Solids
• Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra Livio Zefiro
• VRML polyhedral generator (Conway polyhedron notation)
  • VRML model Chamfered cube
• 3.2.7. Systematic numbering for (C80-Ih) [5,6] fullerene
• Fullerene C80
  1. [3] (Number 7 -Ih)
  2. [4]
• How to make a chamfered cube