Central differencing scheme

Figure 1.Comparison of different schemes

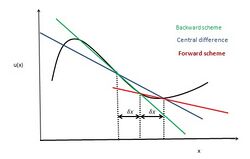
In applied mathematics, the central differencing scheme is a finite difference method that optimizes the approximation for the differential operator in the central node of the considered patch and provides numerical solutions to differential equations. It is one of the schemes used to solve the integrated convection–diffusion equation and to calculate the transported property Φ at the e and w faces, where e and w are short for east and west (compass directions being customarily used to indicate directions on computational grids). The method's advantages are that it is easy to understand and implement, at least for simple material relations; and that its convergence rate is faster than some other finite differencing methods, such as forward and backward differencing. The right side of the convection-diffusion equation, which basically highlights the diffusion terms, can be represented using central difference approximation. To simplify the solution and analysis, linear interpolation can be used logically to compute the cell face values for the left side of this equation, which is nothing but the convective terms. Therefore, cell face values of property for a uniform grid can be written as:

[math]\displaystyle{ \Phi_e = \tfrac 1 2 (\Phi_P + \Phi_E) }[/math] [math]\displaystyle{ \Phi_w = \tfrac 1 2 (\Phi_W + \Phi_P) }[/math]

Steady-state convection diffusion equation

The convection–diffusion equation is a collective representation of diffusion and convection equations, and describes or explains every physical phenomenon involving convection and diffusion in the transference of particles, energy and other physical quantities inside a physical system:

[math]\displaystyle{ \operatorname{div}(\rho u\varphi) = \operatorname{div}(\Gamma\nabla\varphi)+S_\varphi; \, }[/math] where Г is diffusion coefficient and Φ is the property.

Formulation of steady-state convection diffusion equation

Formal integration of steady-state convection–diffusion equation over a control volume gives

[math]\displaystyle{ \int_A \, n\cdot(\rho u\varphi)\,dA = \int_A \,n \cdot (\Gamma\nabla\varphi)\,dA + \int_{CV}\,S_\varphi \,dV }[/math]

(Equation 1)

This equation represents flux balance in a control volume. The left side gives the net convective flux, and the right side contains the net diffusive flux and the generation or destruction of the property within the control volume.

In the absence of source term equation, one becomes

[math]\displaystyle{ \frac{d}{dx} (\rho u\varphi) = \frac{d}{dx}\left( \frac{d\varphi}{dx}\right) }[/math]

(Equation 2)

Continuity equation:

[math]\displaystyle{ {d \over dx}(\rho u)=0 }[/math]

(Equation 3)

Figure 2. Interpolation method

Assuming a control volume and integrating equation 2 over control volume gives:

[math]\displaystyle{ (\rho u\varphi A)_e - (\rho u\varphi A)_w = (\Gamma A d\varphi /dx)_e - (\Gamma A d\varphi /dx)_w }[/math]

(Integrated convection–diffusion equation)

Integration of equation 3 yields:

[math]\displaystyle{ (\rho uA)_e - (\rho uA)_w = 0 }[/math]

(Integrated continuity equation)

It is convenient to define two variables to represent the convective mass flux per unit area and diffusion conductance at cell faces, for example: [math]\displaystyle{ F = \rho u }[/math] [math]\displaystyle{ D = \Gamma / \delta x }[/math]

Assuming [math]\displaystyle{ A_e = A_w }[/math], we can write integrated convection–diffusion equation as: [math]\displaystyle{ F_e \varphi_e - F_w \varphi_w = D_e( \varphi_E - \varphi_P ) - D_w(\varphi_P - \varphi_W) }[/math]

And integrated continuity equation as: [math]\displaystyle{ F_e - F_w = 0 }[/math]

In a central differencing scheme, we try linear interpolation to compute cell face values for convection terms.

For a uniform grid, we can write cell face values of property Φ as [math]\displaystyle{ \varphi_e = \tfrac 1 2 (\varphi_E + \varphi_P), \quad \varphi_w = \tfrac 1 2 (\varphi_P + \varphi_W) }[/math]

On substituting this into integrated convection-diffusion equation, we obtain: [math]\displaystyle{ F_e\frac{\varphi_E + \varphi_P}2 - F_w\frac{\varphi_W + \varphi_P}2 = D_e(\varphi_E - \varphi_P) - D_w(\varphi_P - \varphi_W) }[/math]

And on rearranging: [math]\displaystyle{ \left[\left(D_w + \frac{F_w}2\right) + \left(D_e - \frac{F_e}2\right) + (F_e - F_w)\right]\varphi_P = \left(D_w + \frac{F_w}2 \right)\varphi_W + \left(D_e - \frac{F_e}2 \right)\varphi_E }[/math] [math]\displaystyle{ a_P \varphi_P = a_W \varphi_W + a_E\varphi_E }[/math]

Different aspects of central differencing scheme

Conservativeness

Conservation is ensured in central differencing scheme since overall flux balance is obtained by summing the net flux through each control volume taking into account the boundary fluxes for the control volumes around nodes 1 and 4.

Figure 3.Typical illustration

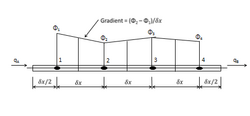
Boundary flux for control volume around node 1 and 4 [math]\displaystyle{ \begin{align} & \left[\frac{\Gamma_{e_1} (\varphi_2 - \varphi_1)}{ \delta x} - q_A\right] + \left[ \frac {\Gamma_{e_2} (\varphi_3 - \varphi_2)}{ \delta x} - \frac{ \Gamma_{w_2} (\varphi_2 - \varphi_1)}{ \delta x}\right] \\[10pt] + {} & \left[ \frac{ \Gamma_{e_3} (\varphi_4 - \varphi_3)}{\delta x} - \frac{\Gamma_{w_3} (\varphi_3 - \varphi_2)}{\delta x}\right] + \left[q_B - \frac{\Gamma_{w_4} (\varphi_4 - \varphi_3)}{\delta x}\right] = q_B - q_A \end{align} }[/math] because [math]\displaystyle{ \Gamma_{e_1} = \Gamma_{w_2} , \Gamma_{e_2} = \Gamma_{w_3} , \Gamma_{e_3} = \Gamma_{w_4} }[/math]

Boundedness

Central differencing scheme satisfies first condition of boundedness.

Since [math]\displaystyle{ F_e - F_w = 0 }[/math] from continuity equation, therefore; [math]\displaystyle{ a_P \varphi_P = a_W \varphi_W + a_E\varphi_E }[/math]

Another essential requirement for boundedness is that all coefficients of the discretised equations should have the same sign (usually all positive). But this is only satisfied when (peclet number) [math]\displaystyle{ F_e/D_e \lt 2 }[/math] because for a unidirectional flow ([math]\displaystyle{ F_e \gt 0, F_w \gt 0 }[/math]) [math]\displaystyle{ a_E = (D_e - F_e/2) }[/math] is always positive if [math]\displaystyle{ D_e \gt F_e/2 }[/math]

Transportiveness

It requires that transportiveness changes according to magnitude of peclet number i.e. when pe is zero [math]\displaystyle{ \varphi }[/math] is spread in all directions equally and as Pe increases (convection > diffusion) [math]\displaystyle{ \varphi }[/math] at a point largely depends on upstream value and less on downstream value. But central differencing scheme does not possess transportiveness at higher pe since Φ at a point is average of neighbouring nodes for all Pe.

Accuracy

The Taylor series truncation error of the central differencing scheme is second order. Central differencing scheme will be accurate only if Pe < 2. Owing to this limitation, central differencing is not a suitable discretisation practice for general purpose flow calculations.

Applications of central differencing schemes

• They are currently used on a regular basis in the solution of the Euler equations and Navier–Stokes equations.
• Results using central differencing approximation have shown noticeable improvements in accuracy in smooth regions.
• Shock wave representation and boundary-layer definition can be improved on coarse meshes.

Advantages

• Simpler to program, requires less computer time per step, and works well with multigrid acceleration techniques
• Has a free parameter in conjunction with the fourth-difference dissipation, which is needed to approach a steady state.
• More accurate than the first-order upwind scheme if the Peclet number is less than 2.

Disadvantages

• Somewhat more dissipative
• Leads to oscillations in the solution or divergence if the local Peclet number is larger than 2.

See also

• Finite difference method
• Finite difference
• Taylor series
• Taylor theorem
• Convection–diffusion equation
• Diffusion
• Convection
• Peclet number
• Linear interpolation
• Symmetric derivative
• Upwind differencing scheme for convection

Further reading

• Computational Fluid Dynamics: The Basics with Applications – John D. Anderson, ISBN:0-07-001685-2
• Computational Fluid Dynamics volume 1 – Klaus A. Hoffmann, Steve T. Chiang, ISBN:0-9623731-0-9

External links

• One-Dimensional_Steady-State_Convection_and_Diffusion#Central_Difference_Scheme
• Finite Differences
• Central Difference Methods
• A Conservative Finite Difference Scheme for Poisson–Nernst–Planck Equations