Chemistry:Activated complex
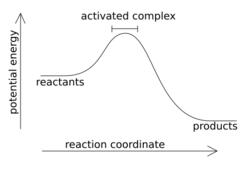
In chemistry, an activated complex represents a collection of intermediate structures in a chemical reaction when bonds are breaking and forming. The activated complex is an arrangement of atoms in an arbitrary region near the saddle point of a potential energy surface.[1] The region represents not one defined state, but a range of unstable configurations that a collection of atoms pass through between the reactants and products of a reaction. Activated complexes have partial reactant and product character, which can significantly impact their behaviour in chemical reactions.[2]
The terms activated complex and transition state are often used interchangeably, but they represent different concepts.[3] Transition states only represent the highest potential energy configuration of the atoms during the reaction, while activated complex refers to a range of configurations near the transition state. In a reaction coordinate, the transition state is the configuration at the maximum of the diagram while the activated complex can refer to any point near the maximum.
Transition state theory (also known as activated complex theory) studies the kinetics of reactions that pass through a defined intermediate state with standard Gibbs energy of activation ΔG°‡.[4] The transition state, represented by the double dagger symbol represents the exact configuration of atoms that has an equal probability of forming either the reactants or products of the given reaction.[5]
The activation energy is the minimum amount of energy to initiate a chemical reaction and form the activated complex.[6] The energy serves as a threshold that reactant molecules must surpass to overcome the energy barrier and transition into the activated complex. Endothermic reactions absorb energy from the surroundings, while exothermic reactions release energy. Some reactions occur spontaneously, while others necessitate an external energy input. The reaction can be visualized using a reaction coordinate diagram to show the activation energy and potential energy throughout the reaction.
Activated complexes were first discussed in transition state theory (also called activated complex theory), which was first developed by Eyring, Evans, and Polanyi in 1935.[7]
Reaction Rate
Transition State Theory
Transition state theory explains the reaction dynamics of reactions. The theory is based on the idea that there is an equilibrium between the activated complex and reactant molecules. The theory incorporates concepts from collision theory, which states that for a reaction to occur, reacting molecules must collide with a minimum energy and correct orientation. The reactants are first transformed into the activated complex before breaking into the products.[6] From the properties of the activated complex and reactants, the reaction rate constant is[math]\displaystyle{ k = K \frac{k_B T}{h} }[/math]where K is the equilibrium constant, [math]\displaystyle{ k_B }[/math] is the Boltzmann constant, T is the thermodynamic temperature, and h is Planck's constant.[8] Transition state theory is based on classical mechanics, as it assumes that as the reaction proceeds, the molecules will never return to the transition state.[9]
Symmetry
An activated complex with high symmetry can decrease the accuracy of rate expressions.[10] Error can arise from introducing symmetry numbers into the rotational partition functions for the reactants and activated complexes. To reduce errors, symmetry numbers can by omitted by multiplying the rate expression by a statistical factor:[math]\displaystyle{ k = l^\ddagger \frac{k_B T}{h} \frac{Q_\ddagger}{Q_A Q_B} e^\left(-\frac{\epsilon}{k_B T}\right) }[/math]where the statistical factor [math]\displaystyle{ l^\ddagger }[/math] is the number of equivalent activated complexes that can be formed, and the Q are the partition functions from the symmetry numbers that have been omitted.[10]
The activated complex is a collection of molecules that forms and then explodes along a particular internal normal coordinate. Ordinary molecules have three translational degrees of freedom, and their properties are similar to activated complexes. However, activated complexed have an extra degree of translation associated with their approach to the energy barrier, crossing it, and then dissociating.[8]
See also
References
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Activated complex". doi:10.1351/goldbook.A00092
- ↑ Peter Atkins and Julio de Paula, Physical Chemistry (8th ed., W.H. Freeman 2006), p.809 ISBN:0-7167-8759-8
- ↑ Tuñón, Iñaki; Williams, Ian H. (2019), "The transition state and cognate concepts", Advances in Physical Organic Chemistry (Elsevier) 53: pp. 29–68, doi:10.1016/bs.apoc.2019.09.001, ISBN 978-0-08-102900-8, https://linkinghub.elsevier.com/retrieve/pii/S0065316019300036
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Transition State Theory". doi:10.1351/goldbook.T06470
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Transition State". doi:10.1351/goldbook.T06468
- ↑ 6.0 6.1 (in en) Chemical Kinetics and Reaction Dynamics. Dordrecht: Springer Netherlands. 2006. doi:10.1007/978-1-4020-4547-9. ISBN 978-1-4020-4546-2. http://link.springer.com/10.1007/978-1-4020-4547-9.
- ↑ Eyring, Henry (1935). "The Activated Complex in Chemical Reactions" (in en). The Journal of Chemical Physics 3 (2): 107–115. doi:10.1063/1.1749604. ISSN 0021-9606. https://pubs.aip.org/jcp/article/3/2/107/203352/The-Activated-Complex-in-Chemical-Reactions.
- ↑ 8.0 8.1 Eyring, Henry. (1935). "The Activated Complex and the Absolute Rate of Chemical Reactions." (in en). Chemical Reviews 17 (1): 65–77. doi:10.1021/cr60056a006. ISSN 0009-2665. https://pubs.acs.org/doi/abs/10.1021/cr60056a006.
- ↑ Pechukas, P (1981). "Transition State Theory" (in en). Annual Review of Physical Chemistry 32 (1): 159–177. doi:10.1146/annurev.pc.32.100181.001111. ISSN 0066-426X.
- ↑ 10.0 10.1 Murrell, J. N.; Laidler, K. J. (1968). "Symmetries of activated complexes" (in en). Transactions of the Faraday Society 64 (0): 371–377. doi:10.1039/TF9686400371. ISSN 0014-7672. https://pubs.rsc.org/en/content/articlelanding/1968/tf/tf9686400371.
 |