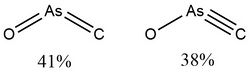Chemistry:Natural resonance theory
In computational chemistry, natural resonance theory (NRT) is an iterative, variational functional embedded into the natural bond orbital (NBO) program, commonly run in Gaussian, GAMESS, ORCA, Ampac and other software packages.[1][2] NRT was developed in 1997 by Frank A. Weinhold and Eric D. Glendening, chemistry professors at University of Wisconsin-Madison and Indiana State University, respectively. Given a list of NBOs for an idealized natural Lewis structure, the NRT functional creates a list of Lewis resonance structures and calculates the resonance weights of each contributing resonance structure.[1] Structural and chemical properties, such as bond order, valency, and bond polarity, may be calculated from resonance weights.[2] Specifically, bond orders may be divided into their covalent and ionic contributions, while valency is the sum of bond orders of a given atom.[2][3] This aims to provide quantitative results that agree with qualitative notions of chemical resonance.[1] In contrast to the "wavefunction resonance theory" (i.e., the superposition of wavefunctions), NRT uses the density matrix resonance theory, performing a superposition of density matrices to realize resonance.[4][5][6] NRT has applications in ab initio calculations,[2][7][6] including calculating the bond orders of intra- and intermolecular interactions[8][9] and the resonance weights of radical isomers.[10]
History
During the 1930s, Professor Linus Pauling and postdoctoral researcher George Wheland applied quantum-mechanical formalism to calculate the resonance energy of organic molecules.[11][12][13] To do this, they estimated the structure and properties of molecules described by more than one Lewis structure as a linear combination of all Lewis structures:
- [math]\displaystyle{ \Psi{_A{}_i}=\sum_{\kappa} a{_i{}_\kappa}\Psi{_a{}_\kappa} }[/math]
where aiκ and Ψaκ denote the weight and single-electron eigenfunction from the wavefunction for a Lewis structure κ, respectively.[1][2][12][14][6] Their formalism assumes that localized valence bond wavefunctions are mutually orthogonal.[1][2]
- [math]\displaystyle{ \langle\Psi_\alpha|\Psi_\beta\rangle=\delta_{\alpha_\beta} }[/math]
While this assumption ensures that the sum of the weights of the resonance structures describing the molecule is one, it creates difficulties in computing aiκ.[1][15] The Pauling-Wheland formalism also assumes that cross-terms from density matrix multiplication may be neglected.[1] This facilitates the averaging of chemical properties, but, like the first assumption, is not true for actual wavefunctions.[1][15] Additionally, in the case of polar bonding, these assumptions necessitate the generation of ionic resonance structures that often overlap with covalent structures.[1] In other words, superfluous resonance structures are calculated for polar molecules. Overall, the Pauling-Wheland formulation of resonance theory was unsuitable for quantitative purposes.[1][16][15][6] Glendening and Weinhold sought to create a new formalism, within their ab initio NBO program, that would provide an accurate quantitative measure of resonance theory, matching chemical intuition.[1][2][3] To do this, instead of evaluating a linear combination of wavefunctions, they express a linear combination of density operators, Γ, (i.e., matrices) for localized structures, where the sum of all weights, ωα, is one.[1][2][3][4][17]
- [math]\displaystyle{ \Gamma=\sum_{\alpha}\omega_\alpha\Gamma_\alpha }[/math] where [math]\displaystyle{ \omega_\alpha\geq0 }[/math] and [math]\displaystyle{ \sum_{\alpha}\omega_\alpha=1 }[/math]
In the context of NBO, the true density operator Γ represents the NBOs of an idealized natural Lewis structure.[1][3] Once NRT has generated a set of density operators, Γα, for localized resonance structures, α, a least-squares variational functional is employed to quantify the resonance weights of each structure.[1] It does this by measuring the variational error, δw, of the linear combination of resonance structures to the true density operator Γ.[1][6]
- [math]\displaystyle{ \delta_W=\underset{\{\omega_\alpha\}}{min}\|\Gamma-\sum_{\alpha}\omega_\alpha\Gamma_\alpha\| }[/math]
To evaluate a single resonance structure, δref, the absolute difference between a single term expansion and the true density operator, approximated as the leading reference structure, can be taken.[1] Now, the extent to which each reference structure represents the true structure may be evaluated as the "fractional improvement", fw.[1]
- [math]\displaystyle{ \delta_{r_{}e_{}f}=\|\Gamma-\Gamma_{r_{}e_{}f}\| }[/math]
- [math]\displaystyle{ f_W= \frac{\delta_{r_{}e_{}f}-\delta_W}{\delta_{r_{}e_{}f}} }[/math]
From this equation, it is evident that as fw approaches one and δw approaches zero, δref becomes a better representation of the true structure.
Updates
In 2019, Glendening, Wright and Weinhold introduced a quadratic programming (QP) strategy for variational minimization in NRT.[17] This new feature is integrated into NBO 7.0 version of their program.[17][18] In this program, the matrix root-mean square deviation (Frobenius norm)[18] of the resonance weights is calculated.
- [math]\displaystyle{ \Delta \omega=\underset{\{\omega_\alpha\}}{min}\left ( \frac{\|\Gamma_{Q_{}C}-\sum_{\alpha}\omega_\alpha\Gamma_\alpha\|^2}{n_b} \right )^\frac{1}{2} }[/math]
The mean-squared density matrices, representing deviation from the true density matrix, may be rewritten as a Gram matrix, and an iterative algorithm is used to minimize the Gram matrix and solve the QP.[17][6]
Theory
Generation of resonance structures and their density matrices
From a given wavefunction, Ψ, a list of optimal NBOs for a Lewis-type wavefunction are generated along with a list of non-Lewis NBOs (e.g., incorporating some antibonding interactions).[3] When these latter orbitals have nonzero value, there is "delocalization" (i.e., deviation from the ideal Lewis-type wavefunction). From this, NRT generates a "delocalization list" from deviation from the parent structure and describes a series of alternative structures reflecting the delocalization.[1][3] A threshold for the number of generated resonance structures can be set by controlling the desired energetic maximum (NRTTHR threshold).[1] The NBOs for a resonance structure formula can then be, subsequently, calculated from the CHOOSE option. Operationally, there are three ways in which alternative resonance structures may be generated: (1) from the LEWIS option, considering the Wiberg bond indices; (2) from the delocalization list; (3) specified by the user.[1]
Below is an example of how NRT may generate a list of resonance structures.
(1) Given an input wavefunction, NRT creates a list of reference Lewis structures. The LEWIS option tests each structure and rejects those that do not conform to the Lewis bonding theory (i.e., those that do not fulfill the octet rule, pose unreasonable formal charges, etc.).
(2) The PARENT and CHOOSE operations determine the optimal set of NBOs corresponding to a specific resonance structure. Additionally, CHOOSE is able to eliminate identical resonance structures.
(3) A user may then call SELECT to select the structure that best matches to the true molecular structure. This option may also show other structures within a defined energy threshold NRTTHR, deviating from optimal Lewis density.
(4) Two other operations, CONDNS and KEKULE, are ran to remove redundant ionic structures and append structures related by bond shifts, respectively.
(5) Lastly, SECRES is called to calculate the NBOs and density matrices of each resonance structure.
Generation of resonance weights
To compute the variational error, δw, NRT offers the following optimization methods: the steepest descent algorithms BFGS and POWELL and a "simulated annealing method" ANNEAL and MULTI.[1] Most commonly, the NRT program computes an initial guess of the resonance weights by the following relation:
- [math]\displaystyle{ \overset{\backsim}{\underset{\alpha}{\omega}}\propto e^{-3\rho_\alpha} }[/math]
where the weight is proportional to the exponential of the non-Lewis density, ρ, of structure α.[1] Then the BFGS and POWELL steepest descent methods optimize for the nearest local minimum in energy.[1]
In contrast, the ANNEAL option finds the global maximum of the fractional improvement, fw, and performs a controlled, iterative random walk across the fw surface. This method is more computationally expensive than the BFGS and POWELL steepest descent methods.[1]
After optimization, SUPPL evaluates the weight of each resonance structure and modifies the list of resonance structures by either retaining or adding resonance structures of high weight and deleting or excluding those of low weight. It continues this process until either convergence is achieved or oscillation occurs.[1]
Updates
In NBO version 7.0, the $NRTSTR function does not need to be called to generate a list of representative resonance structures, and the $CHOOSE algorithm has been adapted to be "essentially identical to the NLS [natural Lewis structure] algorithm", increasing the overall optimization of each resonance structure by reducing the amount to which the parent Lewis structure contributes to the resonance structure.[18][17][6]
Applications
Main group chemistry
Bond order of the pnictogen bond
In 2015, Liu et al.,[8] conducted ab initio MP2/aug-cc-pvDZ calculations and used NRT in NBO version 5.0 to determine the natural bond order (i.e., a measure of electron density) of noncovalent weak "pnicogen bond" interactions—analogous to the hydrogen bond—between various compounds. Their results are summarized in the following table.
| HCHO· · · PH2CH3 | HCHO· · · PH3 | HCHO· · · PH2C6H5 | HCHO· · · PH2Br | HCHO· · · PH2Cl | HCHO· · · PH2F | HCHO· · · PH2NO2 | |
| Covalent Bond order of O· · · P | 0.00001 | 0.00001 | 0.00001 | 0.00001 | 0.00001 | 0.00001 | 0.00001 |
| Ionic Bond order of O· · · P | 0.0021 | 0.0001 | 0.0005 | 0.0088 | 0.0057 | 0.0125 | 0.0055 |
| Total Bond Order of O· · · P | 0.00211 | 0.00011 | 0.00051 | 0.0089 | 0.00571 | 0.0126 | 0.00551 |
These results indicate that the ionic bond order of the O· · · P pnictogen bond is the greatest contribution to the total bond order. Therefore, this weak, noncovalent interaction is primarily electrostatic.[8]
Bond order of Ge2M compounds
In 2018 Minh et al.,[19] used NRT in the NBO 5.G program, with density obtained from the B3P86/6-311+G(d) level of theory, to calculate the bond orders in a series of Ge2M compounds, where M is a first-row transition metal. The results are found in the following table.
| Cluster | Ge-Ge Bond Order | Ge-M Bond Order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total | Covalent | Ionic | %covalency | %ionicity | Total | Covalent | Ionic | %covalency | %ionicity | |
| Ge2Sc | 1.68 | 1.35 | 0.33 | 80.4 | 19.6 | 1.39 | 0.69 | 0.70 | 49.6 | 50.4 |
| Ge2Ti | 1.50 | 1.27 | 0.23 | 84.7 | 15.3 | 1.67 | 0.81 | 0.86 | 48.5 | 51.5 |
| Ge2V | 1.75 | 1.18 | 0.57 | 67.5 | 32.5 | 1.55 | 0.68 | 0.87 | 43.9 | 56.1 |
| Ge2Cr | 2.28 | 2.14 | 0.14 | 93.9 | 6.1 | 0.94 | 0.21 | 0.73 | 22.3 | 77.7 |
| Ge2Mn | 2.36 | 1.88 | 0.48 | 79.7 | 20.3 | 0.84 | 0.32 | 0.52 | 38.1 | 61.9 |
| Ge2Fe | 1.73 | 1.28 | 0.46 | 73.7 | 26.3 | 0.98 | 0.52 | 0.46 | 53.1 | 46.9 |
| Ge2Co | 1.76 | 1.28 | 0.48 | 72.6 | 27.4 | 0.91 | 0.43 | 0.48 | 47.2 | 52.8 |
| Ge2Ni | 1.96 | 1.38 | 0.58 | 70.3 | 29.7 | 0.92 | 0.44 | 0.48 | 47.8 | 52.2 |
| Ge2Cu | 2.38 | 2.17 | 0.21 | 91.2 | 8.8 | 0.65 | 0.21 | 0.44 | 32.3 | 67.7 |
| Ge2Zn | 2.38 | 1.95 | 0.44 | 81.6 | 18.4 | 0.37 | 0.25 | 0.12 | 67.6 | 32.4 |
These results show that the Ge–Ge bond order ranges from 1.5–2.4, while the Ge–M bond order ranges from 0.3–1.7.[19] Furthermore, the Ge–Ge bond is primarily covalent, whereas the Ge–M bond usually has an equal mix of covalent and ionic nature. Exceptions to this are Cr, Mn, and Cu, where the ionic component is dominant because of smaller overlap with the 4s orbital of the M atom, leading to less stability.[19] Interactions with M = Cr, Mn, and Cu are described as an electron transfer from the 4s atomic orbital on the M atom to a pi molecular orbital of the Ge2 fragment.[19] Interactions with the other M atoms are described by two electron transfers: firstly, an electron transfer from the Ge2 fragment into an empty 3d atomic orbital on M and secondly, an electron transfer from the 3d atomic orbital on M into an antibonding orbital on Ge2.[19]
Resonance structures and bond order of regium bonds
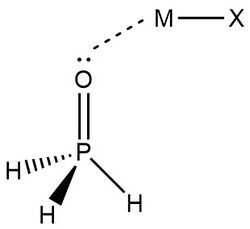
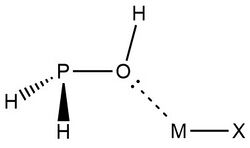
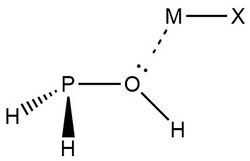
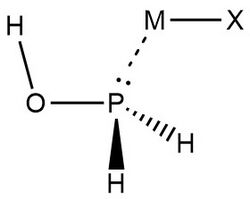
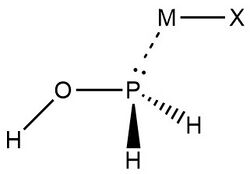
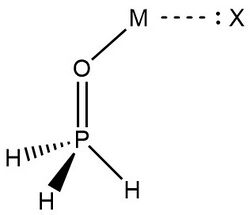
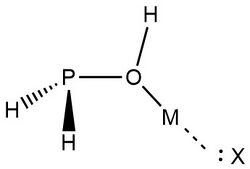
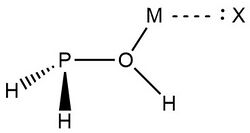
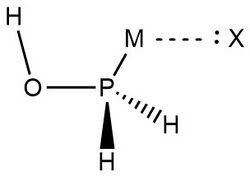
In 2019, Zheng et al.,[9] used NRT at the wB97XD level in the GENBO 6.0W program to generate natural Lewis resonance structures and calculate the bond orders of regium bond interactions between phosphonates and metal halides MX (M = Cu, Ag, Au; X = F, Cl, Br). In a regium bond interaction, electron donors participate in a charge transfer to the metal species.[9] Results of this analysis are shown in the following figures and tables.
| O-I | T-O-II | C-O-III | T-P-II | C-P-III | |
| ωI | |||||
| ωII |
| Resonance Weights | Bond Order | ||||||
| Complex | %ω1 | %ω2 | P–M Bond Order | M–X Bond Order | P–M + M–X Bond Order | ||
| TP-II | Cu-X | T-HOH2P–CuF | 32.53 | 57.34 | 0.68 | 0.36 | 1.04 |
| T-HOH2P–CuCl | 43.58 | 48.39 | 0.57 | 0.47 | 1.04 | ||
| T-HOH2P–CuBr | 46.34 | 45.87 | 0.54 | 0.5 | 1.04 | ||
| Au-X | T-HOH2P–AuF | 30.06 | 57.98 | 0.73 | 0.34 | 1.07 | |
| T-HOH2P–AuCl | 40.22 | 49.35 | 0.62 | 0.45 | 1.07 | ||
| T-HOH2P–AuBr | 43 | 47.25 | 0.59 | 0.48 | 1.07 | ||
| Ag-X | T-HOH2P–AgF | 34.08 | 56.58 | 0.66 | 0.37 | 1.03 | |
| T-HOH2P–AgCl | 44.95 | 47.43 | 0.55 | 0.48 | 1.03 | ||
| T-HOH2P–AgBr | 47.98 | 44.72 | 0.51 | 0.52 | 1.03 | ||
| TO-II | Cu-X | T-–H2PHO–CuF | 92.05 | 3.38 | 0.04 | 0.95 | 0.99 |
| T-H2PHO–CuCl | 92.28 | 3.16 | 0.03 | 0.96 | 0.99 | ||
| T-H2PHO–CuBr | 92.43 | 3.02 | 0.03 | 0.96 | 0.99 | ||
| Au-X | T-H2PHO–AuF | 88.8 | 5.91 | 0.06 | 0.92 | 0.98 | |
| T-H2PHO–AuCl | 89.89 | 4.79 | 0.05 | 0.93 | 0.98 | ||
| T-H2PHO–AuBr | 90.29 | 4.39 | 0.05 | 0.94 | 0.99 | ||
| Ag-X | T-H2PHO–AgF | 93.93 | 2.43 | 0.02 | 0.97 | 0.99 | |
| T-H2PHO–AgCl | 93.87 | 2.26 | 0.02 | 0.97 | 0.99 | ||
| T-H2PHO–AgBr | 93.94 | 2.16 | 0.02 | 0.97 | 0.99 | ||
| CP-III | Cu-X | C-HOH2P–CuF | 32.78 | 56.57 | 0.68 | 0.36 | 1.04 |
| C-HOH2P–CuCl | 43.92 | 47.33 | 0.56 | 0.48 | 1.04 | ||
| C-HOH2P–CuBr | 46.38 | 45.07 | 0.54 | 0.5 | 1.04 | ||
| Au-X | C-HOH2P–AuF | 30.36 | 57.43 | 0.73 | 0.34 | 1.07 | |
| C-HOH2P–AuCl | 40.58 | 48.67 | 0.61 | 0.45 | 1.06 | ||
| C-HOH2P–AuBr | 43.43 | 46.5 | 0.58 | 0.48 | 1.06 | ||
| Ag-X | C-HOH2P–AgF | 34.45 | 55.78 | 0.65 | 0.38 | 1.03 | |
| C-HOH2P–AgCl | 45.83 | 46.02 | 0.53 | 0.5 | 1.03 | ||
| C-HOH2P–AgBr | 48.64 | 43.6 | 0.51 | 0.52 | 1.03 | ||
| CO-III | Cu-X | C-H2PHO–CuF | 61.94 | 33.08 | 0.35 | 0.65 | 1 |
| C-H2PHO–CuCl | 91.48 | 3.35 | 0.04 | 0.95 | 0.99 | ||
| C-H2PHO–CuBr | 91.62 | 3.17 | 0.04 | 0.96 | 1 | ||
| Au-X | C-H2PHO–AuF | 61.78 | 33.11 | 0.35 | 0.65 | 1 | |
| C-H2PHO–AuCl | 88.89 | 5.5 | 0.06 | 0.93 | 0.99 | ||
| C-H2PHO–AuBr | 89.31 | 5.86 | 0.06 | 0.93 | 0.99 | ||
| Ag-X | C-H2PHO–AgF | 93.04 | 2.27 | 0.02 | 0.97 | 0.99 | |
| C-H2PHO–AgCl | 93.09 | 2.18 | 0.02 | 0.97 | 0.99 | ||
| C-H2PHO–AgBr | 93.15 | 2.1 | 0.02 | 0.97 | 0.99 | ||
| PH3O-I | Cu-X | PH3O–CuF | 78.5 | 4.19 | 0.05 | 0.94 | 0.99 |
| PH3O–CuCl | 79.46 | 3.79 | 0.04 | 0.94 | 0.98 | ||
| PH3O–CuBr | 79.74 | 3.61 | 0.02 | 0.95 | 0.97 | ||
| Au-X | PH3O–AuF | 50.54 | 32.41 | 0.37 | 0.6 | 0.97 | |
| PH3O–AuCl | 76.26 | 6.11 | 0.03 | 0.91 | 0.94 | ||
| PH3O–AuBr | 76.75 | 5.5 | 0.06 | 0.92 | 0.98 | ||
| Ag-X | PH3O–AgF | 80.78 | 2.62 | 0.03 | 0.96 | 0.99 | |
| PH3O–AgCl | 80.98 | 2.52 | 0.03 | 0.96 | 0.99 | ||
| PH3O–AgBr | 81.06 | 2.54 | 0.02 | 0.96 | 0.98 | ||
In the case of H3PO:· · · MX complexes, these results indicate that ωI is “the best natural Lewis structure” and the lone pair of electrons on the oxygen atom interact with a MX sigma antibonding orbital.[9]
Zheng et al., also analyzed MX interactions with trans- and cis-phosphinuous acid to compare the electron donating abilities of phosphorus and oxygen atoms. The results above demonstrate that when phosphorus acts as the electron donor the weights of ωI and ωII are similar.[9] This is indicative of 3-center 4-electron bonding models. Despite greater mixing, ωII is determined to be the best natural Lewis structure for both the trans- and cis- complexes, with CuBr and AgBr as the only exceptions. Researchers explain that this result is consistent with analyses showing the preference for phosphorus to form covalent interactions. Overall, "the degree of covalency for P–M bonds decreases in the order of F> Cl > Br, Au > Cu > Ag, while the degree of noncovalent for O–M bonds, there is an increase according to F < Cl < Br, Au < Cu < Ag in the entire family."[9]
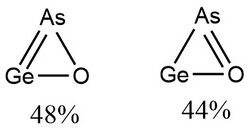
Weight of resonance structures of arsenic radicals
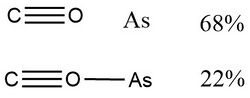
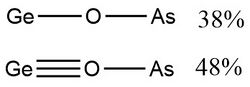
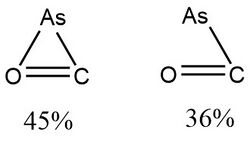
In 2015, Viana et al.,[10] used NRT to determine the weight of resonance structures of the arsenic radical isomers of AsCO, AsSiO and AsGeO, which are of interest in the fields of astrochemistry and astrobiology. The results are shown in the following figures and table.
| AsCO | AsSiO | AsGeO | |
| Isomer 1 | |||
| Isomer 2 | |||
| Isomer 3 | |||
| Isomer 4 |
According to Viana et al., “for most of the isomers, the percentage weight of the secondary resonance structure is negligible. In cyclic structures, the resonance weights lead to very similar percentage values.”[10]
Limitations
Calculating chemical and physical properties by using linear combinations of density matrices, rather than wavefunctions, may result in negative, and therefore erroneous, resonance weights because it is mathematically impossible to expand the density matrix without introducing negative values.[4][5][20]
See also
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 Glendening, E. D.; Weinhold, F. (1998-04-30). <593::aid-jcc3>3.0.co;2-m "Natural resonance theory: I. General formalism". Journal of Computational Chemistry 19 (6): 593–609. doi:10.1002/(sici)1096-987x(19980430)19:6<593::aid-jcc3>3.0.co;2-m. ISSN 0192-8651. http://dx.doi.org/10.1002/(sici)1096-987x(19980430)19:6<593::aid-jcc3>3.0.co;2-m.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Glendening, E. D.; Weinhold, F. (1998-04-30). <610::aid-jcc4>3.0.co;2-u "Natural resonance theory: II. Natural bond order and valency". Journal of Computational Chemistry 19 (6): 610–627. doi:10.1002/(sici)1096-987x(19980430)19:6<610::aid-jcc4>3.0.co;2-u. ISSN 0192-8651. http://dx.doi.org/10.1002/(sici)1096-987x(19980430)19:6<610::aid-jcc4>3.0.co;2-u.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Glendening, Eric D.; Landis, Clark R.; Weinhold, Frank (January 2012). "Natural bond orbital methods" (in en). WIREs Computational Molecular Science 2 (1): 1–42. doi:10.1002/wcms.51. ISSN 1759-0876. https://onlinelibrary.wiley.com/doi/10.1002/wcms.51.
- ↑ 4.0 4.1 4.2 Wang, Yang (2021-03-05). "Superposition of waves or densities: Which is the nature of chemical resonance?" (in en). Journal of Computational Chemistry 42 (6): 412–417. doi:10.1002/jcc.26463. ISSN 0192-8651. PMID 33314179. https://onlinelibrary.wiley.com/doi/10.1002/jcc.26463.
- ↑ 5.0 5.1 Wang, Yang (2021). "A reliable and efficient resonance theory based on analysis of DFT wave functions" (in en). Physical Chemistry Chemical Physics 23 (3): 2331–2348. doi:10.1039/D0CP06207C. ISSN 1463-9076. PMID 33449982. Bibcode: 2021PCCP...23.2331W. http://xlink.rsc.org/?DOI=D0CP06207C.
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Glendening, Eric D.; Landis, Clark R.; Weinhold, Frank (2019-03-13). "Resonance Theory Reboot" (in en). Journal of the American Chemical Society 141 (10): 4156–4166. doi:10.1021/jacs.8b12336. ISSN 0002-7863. PMID 30742414. https://pubs.acs.org/doi/10.1021/jacs.8b12336.
- ↑ Glendening, E. D.; Badenhoop, J. K.; Weinhold, F. (1998-04-30). <628::aid-jcc5>3.0.co;2-t "Natural resonance theory: III. Chemical applications". Journal of Computational Chemistry 19 (6): 628–646. doi:10.1002/(sici)1096-987x(19980430)19:6<628::aid-jcc5>3.0.co;2-t. ISSN 0192-8651. http://dx.doi.org/10.1002/(sici)1096-987x(19980430)19:6<628::aid-jcc5>3.0.co;2-t.
- ↑ 8.0 8.1 8.2 8.3 Liu, Yan-Zhi; Yuan, Kun; Yuan, Zhao; Zhu, Yuan-Cheng; Zhao, Xiang (October 2015). "Theoretical exploration of pnicogen bond noncovalent interactions in HCHO⋯PH2X (X=CH3, H, C6H5, F, Cl, Br, and NO2) complexes" (in en). Journal of Chemical Sciences 127 (10): 1729–1738. doi:10.1007/s12039-015-0933-8. ISSN 0974-3626.
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 Zheng, Baishu; Liu, Yi; Wang, Zhaoxu; Zhou, Fengxiang; Liu, Yuan; Ding, XunLei; Lu, Tian (2019-09-17). "Regium bonds formed by MX (M═Cu, Ag, Au; X═F, Cl, Br) with phosphine-oxide/phosphinous acid: comparisons between oxygen-shared and phosphine-shared complexes" (in en). Molecular Physics 117 (18): 2443–2455. doi:10.1080/00268976.2019.1567847. ISSN 0026-8976. https://www.tandfonline.com/doi/full/10.1080/00268976.2019.1567847.
- ↑ 10.0 10.1 10.2 10.3 Viana, Rommel B.; da Silva, Albérico B.F. (March 2015). "Electronic properties of the AsCO, AsSiO and AsGeO radicals: Linear or cyclic?" (in en). Polyhedron 89: 160–167. doi:10.1016/j.poly.2015.01.010. https://linkinghub.elsevier.com/retrieve/pii/S0277538715000248.
- ↑ Pauling, Linus; Wheland, G. W. (June 1933). "The Nature of the Chemical Bond. V. The Quantum‐Mechanical Calculation of the Resonance Energy of Benzene and Naphthalene and the Hydrocarbon Free Radicals" (in en). The Journal of Chemical Physics 1 (6): 362–374. doi:10.1063/1.1749304. ISSN 0021-9606. Bibcode: 1933JChPh...1..362P. http://aip.scitation.org/doi/10.1063/1.1749304.
- ↑ 12.0 12.1 Pauling, Linus. (April 1931). "The Nature of the Chemical Bond. Application of Results Obtained from the Quantum Mechanics and from a Theory of Paramagnetic Susceptibility to the Structure of Molecules". Journal of the American Chemical Society 53 (4): 1367–1400. doi:10.1021/ja01355a027. ISSN 0002-7863. http://dx.doi.org/10.1021/ja01355a027.
- ↑ Park, Buhm Soon (March 1999). "Chemical translators: Pauling, Wheland and their strategies for teaching the theory of resonance" (in en). The British Journal for the History of Science 32 (1): 21–46. doi:10.1017/S0007087498003471. ISSN 0007-0874. https://www.cambridge.org/core/product/identifier/S0007087498003471/type/journal_article.
- ↑ Simões, Kostas Gavroglu Ana (2012). From Physical Chemistry to Quantum Chemistry: How Chemists Dealt with Mathematics. HYLE Publications, Berlin. OCLC 840819522. http://worldcat.org/oclc/840819522.
- ↑ 15.0 15.1 15.2 Mo, Yirong; Schleyer, Paul von Ragué (2006-02-20). "An Energetic Measure of Aromaticity and Antiaromaticity Based on the Pauling–Wheland Resonance Energies" (in en). Chemistry - A European Journal 12 (7): 2009–2020. doi:10.1002/chem.200500376. ISSN 0947-6539. PMID 16342222.
- ↑ Klein, D.J.; Seitz, W.A. (August 1988). "Pauling—Wheland resonance theory of benzenoid hydrocarbon". Journal of Molecular Structure: THEOCHEM 169: 167–181. doi:10.1016/0166-1280(88)80258-6. ISSN 0166-1280. http://dx.doi.org/10.1016/0166-1280(88)80258-6.
- ↑ 17.0 17.1 17.2 17.3 17.4 Glendening, Eric D.; Wright, Stephen J.; Weinhold, Frank (2019-09-05). "Efficient optimization of natural resonance theory weightings and bond orders by gram‐based convex programming" (in en). Journal of Computational Chemistry 40 (23): 2028–2035. doi:10.1002/jcc.25855. ISSN 0192-8651. PMID 31077408.
- ↑ 18.0 18.1 18.2 Glendening, Eric D.; Landis, Clark R.; Weinhold, Frank (2019-06-07). "NBO 7.0 : New vistas in localized and delocalized chemical bonding theory" (in en). Journal of Computational Chemistry 40 (25): 2234–2241. doi:10.1002/jcc.25873. ISSN 0192-8651. PMID 31172571. https://onlinelibrary.wiley.com/doi/10.1002/jcc.25873.
- ↑ 19.0 19.1 19.2 19.3 19.4 19.5 Minh, Nguyen Duc; Cuong, Chau Hung; Trung, Nguyen Tien; Ngan, Vu Thi (October 2018). "Insight into chemical bonding of the transition metal-doped cluster Ge2M (M = Sc–Zn) series using NBO and NRT theory" (in en). Theoretical Chemistry Accounts 137 (10): 131. doi:10.1007/s00214-018-2326-9. ISSN 1432-881X. http://link.springer.com/10.1007/s00214-018-2326-9.
- ↑ Weinhold, Frank; Glendening, Eric D. (2021). "Comment on "Superposition of Waves or Densities: Which Is the Nature of Chemical Resonance?" [J. Comput. Chem. 2021, 42, 412–417"]. Journal of Computational Chemistry 42 (19): 1338–1340. doi:10.1002/jcc.26696. ISSN 1096-987X. PMID 34041769. https://onlinelibrary.wiley.com/doi/abs/10.1002/jcc.26696.
External links
- Frank Weinhold
- https://www2.chem.wisc.edu/users/weinhold
- https://scholar.google.com/citations?user=47IzzwYAAAAJ&hl=en
- Eric D. Glending
- https://www.indstate.edu/cas/chem_phys/eric-d-glendening
- https://scholar.google.com/citations?user=iRjJ1Y0AAAAJ&hl=en
- Natural Bond Orbital 7.0 Homepage
- https://nbo7.chem.wisc.edu/
 |