Chemistry:Neutralization

Short description: Chemical reaction in which an acid and a base react quantitatively

Animation of a strong acid–strong base neutralization titration (using phenolphthalein). The equivalence point is marked in red.

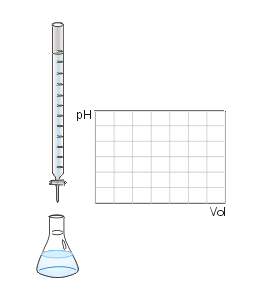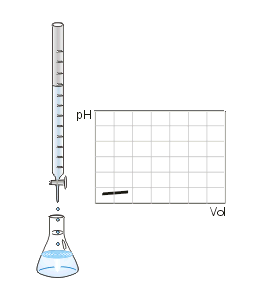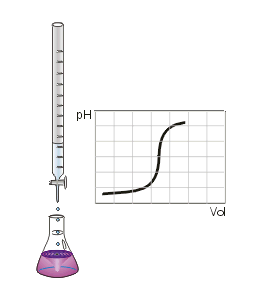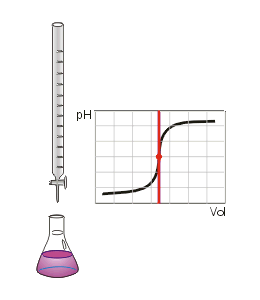
In chemistry, neutralization or neutralisation (see spelling differences) is a chemical reaction in which acid and a base react with an equivalent quantity of each other. In a reaction in water, neutralization results in there being no excess of hydrogen or hydroxide ions present in the solution. The pH of the neutralized solution depends on the acid strength of the reactants.

Meaning of "neutralization"

In the context of a chemical reaction the term neutralization is used for a reaction between an acid and a base or alkali. Historically, this reaction was represented as

acid + base (alkali) → salt + water

[math]\ce{ \mathit{x}H_\mathit{y}A{} + \mathit{y}B(OH)_\mathit{x}{} -> B_\mathit{y}A_\mathit{x}{} + \mathit{xy}H2O }[/math]

For example:

HCl + NaOH → NaCl + H₂O

The statement is still valid as long as it is understood that in an aqueous solution the substances involved are subject to dissociation, which changes the ionization state of the substances. The arrow sign, →, is used because the reaction is complete, that is, neutralization is a quantitative reaction. A more general definition is based on Brønsted–Lowry acid–base theory.

AH + B → A + BH

Electrical charges are omitted from generic expressions such as this, as each species A, AH, B, or BH may or may not carry an electrical charge. Neutralization of sulfuric acid provides a specific example. Two partial neutralization reactions are possible in this instance.

H₂SO₄ + OH⁻ → HSO−4 + H₂O

HSO−4 + OH⁻ → SO2−4 + H₂O

Overall: H₂SO₄ + 2 OH⁻ → SO2−4+ 2 H₂O

After an acid AH has been neutralized there are no molecules of the acid (or hydrogen ions produced by dissociation of the molecule) left in solution.

When an acid is neutralized the amount of base added to it must be equal to the amount of acid present initially. This amount of base is said to be the equivalent amount. In a titration of an acid with a base, the point of neutralization can also be called the equivalence point. The quantitative nature of the neutralization reaction is most conveniently expressed in terms of the concentrations of acid and alkali. At the equivalence point:

volume (acid) × concentration (H⁺ ions from dissociation) = volume (base) × concentration (OH⁻ ions)

In general, for an acid AH_n at concentration c₁ reacting with a base B(OH)_m at concentration c₂ the volumes are related by:

n v₁ c₁ = m v₂ c₂

An example of a base being neutralized by an acid is as follows.

Ba(OH)₂ + 2 H⁺ → Ba²⁺ + 2 H₂O

The same equation relating the concentrations of acid and base applies. The concept of neutralization is not limited to reactions in solution. For example, the reaction of limestone with acid such as sulfuric acid is also a neutralization reaction.

[Ca,Mg]CO₃(s) + H₂SO₄(aq) → (Ca²⁺, Mg²⁺)(aq) + SO2−4(aq) + CO₂(g) + H₂O

Such reactions are important in soil chemistry.

Strong acids and strong bases

A strong acid is one that is fully dissociated in aqueous solution. For example, hydrochloric acid, HCl, is a strong acid.

HCl(aq) → H⁺(aq) + Cl⁻(aq)

A strong base is one that is fully dissociated in aqueous solution. For example, sodium hydroxide, NaOH, is a strong base.

NaOH(aq) → Na⁺(aq) + OH⁻(aq)

Therefore, when a strong acid reacts with a strong base the neutralization reaction can be written as

H⁺ + OH⁻ → H₂O

For example, in the reaction between hydrochloric acid and sodium hydroxide the sodium and chloride ions, Na⁺ and Cl⁻ take no part in the reaction. The reaction is consistent with the Brønsted–Lowry definition because in reality the hydrogen ion exists as the hydronium ion, so that the neutralization reaction may be written as

H₃O⁺ + OH⁻ → H₂O + H₂O

When a strong acid is neutralized by a strong base there are no excess hydrogen ions left in the solution. The solution is said to be neutral as it is neither acidic nor alkaline. The pH of such a solution is close to a value of 7; the exact pH value is dependent on the temperature of the solution.

Neutralization is an exothermic reaction. The standard enthalpy change for the reaction H⁺ + OH⁻ → H₂O is −57.30 kJ/mol.

Quantitative treatment

The term fully dissociated is applied to a solute when the concentration of undissociated solute is below the detection limits, that is, when the undissociated solute's concentration is too low to measured. Quantitatively, this is expressed as log K < −2, or in some texts log K < −1.76. This means that the value of the dissociation constant cannot be obtained from experimental measurements. The value can, however, be estimated theoretically. For example the value of log K ≈ −6 has been estimated for hydrogen chloride in aqueous solution at room temperature. A chemical compound may behave as a strong acid in solution when its concentration is low and as a weak acid when its concentration is very high. Sulfuric acid is an example of such a compound.

Weak acids and strong bases

A weak acid HA is one that does not dissociate fully when it is dissolved in water. Instead an equilibrium mixture is formed:

HA + H₂O ⇌ H₃O⁺ + A⁻

Acetic acid is an example of a weak acid. The pH of the neutralized solution resulting from

HA + OH⁻ → H₂O + A⁻

is not close to 7, as with a strong acid, but depends on the acid dissociation constant, K_a, of the acid. The pH at the end-point or equivalence point in a titration may be calculated as follows. At the end-point the acid is completely neutralized so the analytical hydrogen ion concentration, T_H, is zero and the concentration of the conjugate base, A⁻, is equal to the analytical or formal concentration T_A of the acid: [A⁻] = T_A. When a solution of an acid, HA, is at equilibrium, by definition the concentrations are related by the expression

[A⁻][H⁺] = K_a [HA]; pK_a = −log K_a

The solvent (e.g. water) is omitted from the defining expression on the assumption that its concentration is very much greater than the concentration of dissolved acid, [H₂O] ≫ T_A. The equation for mass-balance in hydrogen ions can then be written as

T_H = [H⁺] + [A⁻][H⁺]/K_a − K_w/[H⁺]

Titration curves for addition of a strong base to a weak acid with pK_a of 4.85. The curves are labelled with the concentration of the acid.

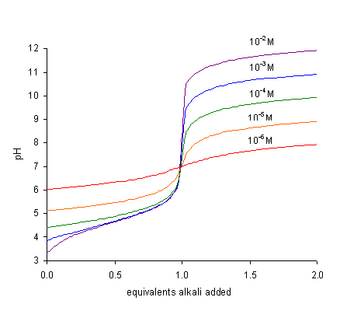
where K_w represents the self-dissociation constant of water. Since K_w = [H⁺][OH⁻], the term K_w/[H⁺] is equal to [OH⁻], the concentration of hydroxide ions. At neutralization, T_H is zero. After multiplying both sides of the equation by [H⁺], it becomes

[H⁺]² + T_A[H⁺]²/K_a − K_w = 0

and, after rearrangement and taking logarithms,

pH = 1/2 pK_w + 1/2 log (1 + T_A/K_a)

With a dilute solution of the weak acid, the term 1 + T_A/K_a is equal to T_A/K_a to a good approximation. If pK_w = 14,

pH = 7 + (pK_a + log T_A)/2

This equation explains the following facts:

• The pH at the end-point depends mainly on the strength of the acid, pK_a.
• The pH at the end-point is greater than 7 and increases with increasing concentration of the acid, T_A, as seen in the figure.

In a titration of a weak acid with a strong base the pH rises more steeply as the end-point is approached. At the end-point, the slope of the curve of pH with respect to amount of titrant is a maximum. Since the end-point occurs at pH greater than 7, the most suitable indicator to use is one, like phenolphthalein, that changes color at high pH.

Weak bases and strong acids

The situation is analogous to that of weak acids and strong bases.

B + H₃O⁺ ⇌ BH⁺ + H₂O

Amines are examples of weak bases. The pH of the neutralized solution depends on the acid dissociation constant of the protonated base, pK_a, or, equivalently, on the base association constant, pK_b. The most suitable indicator to use for this type of titration is one, such as methyl orange, that changes color at low pH.

Weak acids and weak bases

When a weak acid reacts with an equivalent amount of a weak base,

HA + B ⇌ A⁻ + BH⁺

complete neutralization does not always occur. The concentrations of the species in equilibrium with each other will depend on the equilibrium constant, K, for the reaction, which is defined as follows:

[A⁻][BH⁺] = K [HA][B].

The neutralization reaction can be considered as the difference of the following two acid dissociation reactions

HA ⇌ H⁺ + A⁻  K_a,A = [A⁻][H⁺]/[HA]

BH⁺ ⇌ B + H⁺  K_a,B = [B][H⁺]/[BH⁺]

with the dissociation constants K_a,A and K_a,B of the acids HA and BH⁺, respectively. Inspection of the reaction quotients shows that

K = K_a,A/K_a,B.

A weak acid cannot always be neutralized by a weak base, and vice versa. However, for the neutralization of benzoic acid (K_a,A = 6.5 × 10⁻⁵) with ammonia (K_a,B = 5.6 × 10⁻¹⁰ for ammonium), K = 1.2 × 10⁵ >> 1, and more than 99% of the benzoic acid is converted to benzoate.

Applications

Chemical titration methods are used for analyzing acids or bases to determine the unknown concentration. Either a pH meter or a pH indicator which shows the point of neutralization by a distinct color change can be employed. Simple stoichiometric calculations with the known volume of the unknown and the known volume and molarity of the added chemical gives the molarity of the unknown.

In wastewater treatment, chemical neutralization methods are often applied to reduce the damage that an effluent may cause upon release to the environment. For pH control, popular chemicals include calcium carbonate, calcium oxide, magnesium hydroxide, and sodium bicarbonate. The selection of an appropriate neutralization chemical depends on the particular application.

There are many uses of neutralization reactions that are acid-alkali reactions. A very common use is antacid tablets. These are designed to neutralize excess gastric acid in the stomach (HCl) that may be causing discomfort in the stomach or lower esophagus. This can also be remedied by the ingestion of sodium bicarbonate (NaHCO₃). Sodium bicarbonate is also commonly used to neutralise acid spills in laboratories, as well as acid burns.

In chemical synthesis of nanomaterials, the heat of neutralization reaction can be used to facilitate the chemical reduction of metal precursors.

Also in the digestive tract, neutralization reactions are used when food is moved from the stomach to the intestines. In order for the nutrients to be absorbed through the intestinal wall, an alkaline environment is needed, so the pancreas produce an antacid bicarbonate to cause this transformation to occur.

Another common use, though perhaps not as widely known, is in fertilizers and control of soil pH. Slaked lime (calcium hydroxide) or limestone (calcium carbonate) may be worked into soil that is too acidic for plant growth. Fertilizers that improve plant growth are made by neutralizing sulfuric acid (H₂SO₄) or nitric acid (HNO₃) with ammonia gas (NH₃), making ammonium sulfate or ammonium nitrate. These are salts utilized in the fertilizer.

Industrially, a by-product of the burning of coal, sulfur dioxide gas, may combine with water vapor in the air to eventually produce sulfuric acid, which falls as acid rain. To prevent the sulfur dioxide from being released, a device known as a scrubber gleans the gas from smoke stacks. This device first blows calcium carbonate into the combustion chamber where it decomposes into calcium oxide (lime) and carbon dioxide. This lime then reacts with the sulfur dioxide produced forming calcium sulfite. A suspension of lime is then injected into the mixture to produce a slurry, which removes the calcium sulfite and any remaining unreacted sulfur dioxide.

Further reading

Neutralization is covered in most general chemistry textbooks. Detailed treatments may be found in textbooks on analytical chemistry such as

• Skoog, D.A; West, D.M.; Holler, J.F.; Crouch, S.R. (2004). Fundamentals of Analytical Chemistry (8th ed.). Thomson Brooks/Cole. ISBN 0-03-035523-0.  Chapters 14, 15 and 16

Applications

• Stumm, W.; Morgan, J.J. (1996). Water Chemistry. New York: Wiley. ISBN 0-471-05196-9. https://archive.org/details/waterchemistry00snoerich. 
• Snoeyink, V.L.; Jenkins, D. (1980). Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters. New York: Wiley. ISBN 0-471-51185-4. 
• Millero, F.J. (2006). Chemical Oceanography (3rd ed.). London: Taylor and Francis. ISBN 0-8493-2280-4. 
• Metcalf & Eddy. Wastewater Engineering, Treatment and Reuse. 4th ed. New York: McGraw-Hill, 2003. 526-532.