Halved cube graph
| Halved cube graph | |
|---|---|
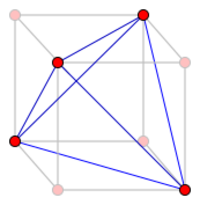 The halved cube graph 1/2Q3 | |
| Vertices | 2n–1 |
| Edges | n(n – 1)2n–3 |
| Automorphisms | n! 2n–1, for n > 4 n! 2n, for n = 4 (2n–1)!, for n < 4[1] |
| Properties | Symmetric Distance regular |
| Notation | 1/2Qn |
| Table of graphs and parameters | |
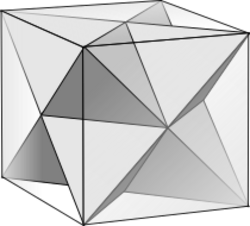
In graph theory, the halved cube graph or half cube graph of dimension n is the graph of the demihypercube, formed by connecting pairs of vertices at distance exactly two from each other in the hypercube graph. That is, it is the half-square of the hypercube. This connectivity pattern produces two isomorphic graphs, disconnected from each other, each of which is the halved cube graph.
Equivalent constructions
The construction of the halved cube graph can be reformulated in terms of binary numbers. The vertices of a hypercube may be labeled by binary numbers in such a way that two vertices are adjacent exactly when they differ in a single bit. The demicube may be constructed from the hypercube as the convex hull of the subset of binary numbers with an even number of nonzero bits (the evil numbers), and its edges connect pairs of numbers whose Hamming distance is exactly two.[2]
It is also possible to construct the halved cube graph from a lower-dimensional hypercube graph, without taking a subset of the vertices:
where the superscript 2 denotes the square of the hypercube graph Qn − 1, the graph formed by connecting pairs of vertices whose distance is at most two in the original graph. For instance, the halved cube graph of dimension four may be formed from an ordinary three-dimensional cube by keeping the cube edges and adding edges connecting pairs of vertices that are on opposite corners of the same square face.
Examples
The halved cube graph of dimension 3 is the complete graph K4, the graph of the tetrahedron. The halved cube graph of dimension 4 is K2,2,2,2, the graph of the four-dimensional regular polytope, the 16-cell. The halved cube graph of dimension five is sometimes known as the Clebsch graph, and is the complement of the folded cube graph of dimension five, which is the one more commonly called the Clebsch graph. It exists in the 5-dimensional uniform 5-polytope, the 5-demicube.
Properties
Because it is the bipartite half of a distance-regular graph, the halved cube graph is itself distance-regular.[3] And because it contains a hypercube as a spanning subgraph, it inherits from the hypercube all monotone graph properties, such as the property of containing a Hamiltonian cycle.
As with the hypercube graphs, and their isometric (distance-preserving) subgraphs the partial cubes, a halved cube graph may be embedded isometrically into a real vector space with the Manhattan metric (L1 distance function). The same is true for the isometric subgraphs of halved cube graphs, which may be recognized in polynomial time; this forms a key subroutine for an algorithm which tests whether a given graph may be embedded isometrically into a Manhattan metric.[4]
For every halved cube graph of dimension five or more, it is possible to (improperly) color the vertices with two colors, in such a way that the resulting colored graph has no nontrivial symmetries. For the graphs of dimension three and four, four colors are needed to eliminate all symmetries.[5]
Sequence
The two graphs shown are symmetric Dn and Bn Petrie polygon projections (2(n − 1) and n dihedral symmetry) of the related polytope which can include overlapping edges and vertices.
| n | Polytope | Graph | Vertices | Edges |
|---|---|---|---|---|
| 2 | Line segment |  |
2 | – |
| 3 | tetrahedron |   |
4 | 6 |
| 4 | 16-cell |   |
8 | 24 |
| 5 | 5-demicube | 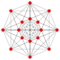 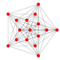 |
16 | 80 |
| 6 | 6-demicube |  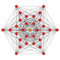 |
32 | 240 |
| 7 | 7-demicube |  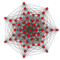 |
64 | 672 |
| 8 | 8-demicube | 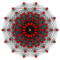 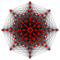 |
128 | 1792 |
| 9 | 9-demicube |   |
256 | 4608 |
| 10 | 10-demicube |   |
512 | 11520 |
References
- ↑ A.E. Brouwer, A.M. Cohen, and A. Neumaier (1989), Distance Regular Graphs. Berlin, New York: Springer-Verlag, p. 265. ISBN 3-540-50619-5, ISBN 0-387-50619-5
- ↑ "Low-distortion embeddings of finite metric spaces", Handbook of Discrete and Computational Geometry (2nd ed.), CRC Press, 2010, p. 179, ISBN 9781420035315, https://books.google.com/books?hl=en&lr=&id=QS6vnl8WlnQC&oi=fnd&pg=PA179.
- ↑ Chihara, Laura; Stanton, Dennis (1986), "Association schemes and quadratic transformations for orthogonal polynomials", Graphs and Combinatorics 2 (2): 101–112, doi:10.1007/BF01788084.
- ↑ "Recognition of the l1-graphs with complexity O(nm), or football in a hypercube", European Journal of Combinatorics 17 (2-3): 279–289, 1996, doi:10.1006/eujc.1996.0024.
- ↑ Bogstad, Bill (2004), "The distinguishing number of the hypercube", Discrete Mathematics 283 (1-3): 29–35, doi:10.1016/j.disc.2003.11.018.
External links
 |
