Conical coordinates

Coordinate surfaces of the conical coordinates. The constants b and c were chosen as 1 and 2, respectively. The red sphere represents r = 2, the blue elliptic cone aligned with the vertical z-axis represents μ=cosh(1) and the yellow elliptic cone aligned with the (green) x-axis corresponds to ν² = 2/3. The three surfaces intersect at the point P (shown as a black sphere) with Cartesian coordinates roughly (1.26, -0.78, 1.34). The elliptic cones intersect the sphere in spherical conics.

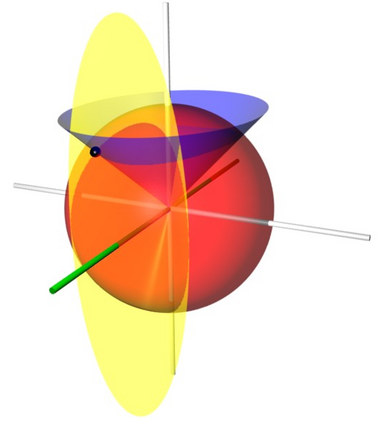
Conical coordinates, sometimes called sphero-conal or sphero-conical coordinates, are a three-dimensional orthogonal coordinate system consisting of concentric spheres (described by their radius r) and by two families of perpendicular elliptic cones, aligned along the z- and x-axes, respectively. The intersection between one of the cones and the sphere forms a spherical conic.

Basic definitions

The conical coordinates [math]\displaystyle{ (r, \mu, \nu) }[/math] are defined by

[math]\displaystyle{ x = \frac{r\mu\nu}{bc} }[/math]

[math]\displaystyle{ y = \frac{r}{b} \sqrt{\frac{\left( \mu^{2} - b^{2} \right) \left( \nu^{2} - b^{2} \right)}{\left( b^{2} - c^{2} \right)} } }[/math]

[math]\displaystyle{ z = \frac{r}{c} \sqrt{\frac{\left( \mu^{2} - c^{2} \right) \left( \nu^{2} - c^{2} \right)}{\left( c^{2} - b^{2} \right)} } }[/math]

with the following limitations on the coordinates

[math]\displaystyle{ \nu^{2} \lt c^{2} \lt \mu^{2} \lt b^{2}. }[/math]

Surfaces of constant r are spheres of that radius centered on the origin

[math]\displaystyle{ x^{2} + y^{2} + z^{2} = r^{2}, }[/math]

whereas surfaces of constant [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \nu }[/math] are mutually perpendicular cones

[math]\displaystyle{ \frac{x^{2}}{\mu^{2}} + \frac{y^{2}}{\mu^{2} - b^{2}} + \frac{z^{2}}{\mu^{2} - c^{2}} = 0 }[/math]

and

[math]\displaystyle{ \frac{x^{2}}{\nu^{2}} + \frac{y^{2}}{\nu^{2} - b^{2}} + \frac{z^{2}}{\nu^{2} - c^{2}} = 0. }[/math]

In this coordinate system, both Laplace's equation and the Helmholtz equation are separable.

Scale factors

The scale factor for the radius r is one (h_r = 1), as in spherical coordinates. The scale factors for the two conical coordinates are

[math]\displaystyle{ h_{\mu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \mu^{2} \right) \left( \mu^{2} - c^{2} \right)}} }[/math]

and

[math]\displaystyle{ h_{\nu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \nu^{2} \right) \left( c^{2} - \nu^{2} \right)}}. }[/math]

Bibliography

• Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 659. ISBN 0-07-043316-X. 
• Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 183–184. https://archive.org/details/mathematicsofphy0002marg. 
• Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 179. ASIN B0000CKZX7. 
• Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 991–100. 
• Arfken G (1970). Mathematical Methods for Physicists (2nd ed.). Orlando, FL: Academic Press. pp. 118–119. ASIN B000MBRNX4. 
• Moon P, Spencer DE (1988). "Conical Coordinates (r, θ, λ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 37–40 (Table 1.09). ISBN 978-0-387-18430-2. 

External links

• MathWorld description of conical coordinates