Spherical conic

In mathematics, a spherical conic or sphero-conic is a curve on the sphere, the intersection of the sphere with a concentric elliptic cone. It is the spherical analog of a conic section (ellipse, parabola, or hyperbola) in the plane, and as in the planar case, a spherical conic can be defined as the locus of points the sum or difference of whose great-circle distances to two foci is constant.[1] By taking the antipodal point to one focus, every spherical ellipse is also a spherical hyperbola, and vice versa. As a space curve, a spherical conic is a quartic, though its orthogonal projections in three principal axes are planar conics. Like planar conics, spherical conics also satisfy a "reflection property": the great-circle arcs from the two foci to any point on the conic have the tangent and normal to the conic at that point as their angle bisectors.
Many theorems about conics in the plane extend to spherical conics. For example, Graves's theorem and Ivory's theorem about confocal conics can also be proven on the sphere; see confocal conic sections about the planar versions.[2]
Just as the arc length of an ellipse is given by an incomplete elliptic integral of the second kind, the arc length of a spherical conic is given by an incomplete elliptic integral of the third kind.[3]
An orthogonal coordinate system in Euclidean space based on concentric spheres and quadratic cones is called a conical or sphero-conical coordinate system. When restricted to the surface of a sphere, the remaining coordinates are confocal spherical conics. Sometimes this is called an elliptic coordinate system on the sphere, by analogy to a planar elliptic coordinate system. Such coordinates can be used in the computation of conformal maps from the sphere to the plane.[4]
Applications
The solution of the Kepler problem in a space of uniform positive curvature is a spherical conic, with a potential proportional to the cotangent of geodesic distance.[5]
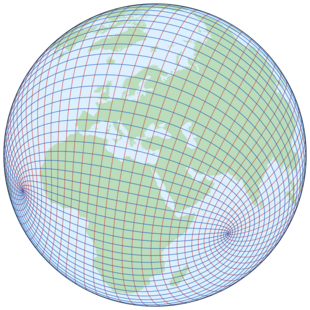
Because it preserves distances to a pair of specified points, the two-point equidistant projection maps the family of confocal conics on the sphere onto two families of confocal ellipses and hyperbolae in the plane.[6]
If a portion of the Earth is modeled as spherical, e.g. using the osculating sphere at a point on an ellipsoid of revolution, the hyperbolae used in hyperbolic navigation (which determines position based on the difference in received signal timing from fixed radio transmitters) are spherical conics.[7]
Notes
- ↑ Fuss, Nicolas (1788). "De proprietatibus quibusdam ellipseos in superficie sphaerica descriptae" (in la). Nova Acta academiae scientiarum imperialis Petropolitanae 3: 90–99. https://archive.org/details/novaactaacademia03impe/page/90/.
- ↑ Stachel, Hellmuth; Wallner, Johannes (2004). "Ivory's theorem in hyperbolic spaces". Siberian Mathematical Journal 45 (4): 785–794. http://www.geometrie.tugraz.at/wallner/h_ivory.pdf.
- ↑
Gudermann, Christoph (1835). "Integralia elliptica tertiae speciei reducendi methodus simplicior, quae simul ad ipsorum applicationem facillimam et computum numericum expeditum perducit. Sectionum conico–sphaericarum qudratura et rectification". Crelle's Journal 14: 169–181. https://archive.org/details/journalfrdierei19crelgoog/page/n178/.
Booth, James (1844). "IV. On the rectification and quadrature of the spherical ellipse". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 25 (163): 18–38. doi:10.1080/14786444408644925. - ↑
Guyou, Émile (1887). "Nouveau système de projection de la sphère: Généralisation de la projection de Mercator" (in fr). Annales Hydrographiques. Ser. 2 9: 16–35. https://www.retronews.fr/journal/annales-hydrographiques/1-janvier-1887/1877/4868382/23.
Adams, Oscar Sherman (1925). Elliptic functions applied to conformal world maps. US Government Printing Office. US Coast and Geodetic Survey Special Publication No. 112. https://library.oarcloud.noaa.gov/docs.lib/htdocs/rescue/cgs_specpubs/QB275U35no1121925.pdf. - ↑
Higgs, Peter W. (1979). "Dynamical symmetries in a spherical geometry I". Journal of Physics A: Mathematical and General 12 (3): 309–323. doi:10.1088/0305-4470/12/3/006.
Kozlov, Valery Vasilevich; Harin, Alexander O. (1992). "Kepler's problem in constant curvature spaces". Celestial Mechanics and Dynamical Astronomy 54 (4): 393–399. doi:10.1007/BF00049149.
Cariñena, José F.; Rañada, Manuel F.; Santander, Mariano (2005). "Central potentials on spaces of constant curvature: The Kepler problem on the two-dimensional sphere S2 and the hyperbolic plane H2". Journal of Mathematical Physics 46 (5): 052702. doi:10.1063/1.1893214.
Arnold, Vladimir; Kozlov, Valery Vasilevich; Neishtadt, Anatoly I. (2007). Mathematical Aspects of Classical and Celestial Mechanics. doi:10.1007/978-3-540-48926-9.
Diacu, Florin (2013). "The curved N-body problem: risks and rewards". Mathematical Intelligencer 35 (3): 24–33. https://www.math.uvic.ca/faculty/diacu/Math-Intell.pdf. - ↑ Cox, Jacques-François (1946). "The doubly equidistant projection". Bulletin Géodésique 2 (1): 74–76. doi:10.1007/bf02521618.
Further reading
- Chasles, Michel (1831) (in fr). Mémoire de géométrie sur les propriétés générales des coniqes sphériques. L'Académie de Bruxelles. https://archive.org/details/mmoiredegomtrie00chasgoog/. English edition:
- Chasles, Michel (1860). "Résumé d'une théorie des coniques sphériques homofocales" (in fr). Comptes rendus de l'Académie des Sciences 50: 623–633. https://archive.org/details/comptesrendusheb50acad/page/623/. Republished in Journal de mathématiques pures et appliquées. Ser. 2. 5: 425-454. PDF from mathdoc.fr.
- Glaeser, Georg; Stachel, Hellmuth; Odehnal, Boris (2016). "10.1 Spherical conics". The Universe of Conics: From the ancient Greeks to 21st century developments. Springer.. pp. 436–467. doi:10.1007/978-3-662-45450-3_10.
- Izmestiev, Ivan (2019). "Spherical and hyperbolic conics". Eighteen Essays in Non-Euclidean Geometry. European Mathematical Society. pp. 262–320. doi:10.4171/196-1/15. https://arxiv.org/abs/1702.06860.
- Salmon, George (1927). "X. Cones and Sphero-Conics". A Treatise on the Analytic Geometry of Three Dimensions (7th ed.). Chelsea. pp. 249–267. https://archive.org/details/treatiseonanalyt00salm_0/page/249.
- Story, William Edward (1882). "On non-Euclidean properties of conics". American Journal of Mathematics 5 (1): 358–381. doi:10.2307/2369551. https://www.jstor.org/stable/pdf/2369551.pdf.
- Sykes, Gerrit Smith (1877). "Spherical Conics". Proceedings of the American Academy of Arts and Sciences 13: 375–395. doi:10.2307/25138501. https://archive.org/details/proceedingsofame1877amer/page/375.
- Tranacher, Harald (2006). Sphärische Kegelschnitte – didaktisch aufbereitet [Spherical conics – didactically prepared] (PDF) (Thesis) (in Deutsch). Technischen Universität Wien.
 |
