Orthogonal coordinates

Short description: Set of coordinates where the coordinate hypersurfaces all meet at right angles

In mathematics, orthogonal coordinates are defined as a set of d coordinates [math]\displaystyle{ \mathbf q = (q^1, q^2, \dots, q^d) }[/math] in which the coordinate hypersurfaces all meet at right angles (note that superscripts are indices, not exponents). A coordinate surface for a particular coordinate q^k is the curve, surface, or hypersurface on which q^k is a constant. For example, the three-dimensional Cartesian coordinates (x, y, z) is an orthogonal coordinate system, since its coordinate surfaces x = constant, y = constant, and z = constant are planes that meet at right angles to one another, i.e., are perpendicular. Orthogonal coordinates are a special but extremely common case of curvilinear coordinates.

Motivation

A conformal map acting on a rectangular grid. Note that the orthogonality of the curved grid is retained.

While vector operations and physical laws are normally easiest to derive in Cartesian coordinates, non-Cartesian orthogonal coordinates are often used instead for the solution of various problems, especially boundary value problems, such as those arising in field theories of quantum mechanics, fluid flow, electrodynamics, plasma physics and the diffusion of chemical species or heat.

The chief advantage of non-Cartesian coordinates is that they can be chosen to match the symmetry of the problem. For example, the pressure wave due to an explosion far from the ground (or other barriers) depends on 3D space in Cartesian coordinates, however the pressure predominantly moves away from the center, so that in spherical coordinates the problem becomes very nearly one-dimensional (since the pressure wave dominantly depends only on time and the distance from the center). Another example is (slow) fluid in a straight circular pipe: in Cartesian coordinates, one has to solve a (difficult) two dimensional boundary value problem involving a partial differential equation, but in cylindrical coordinates the problem becomes one-dimensional with an ordinary differential equation instead of a partial differential equation.

The reason to prefer orthogonal coordinates instead of general curvilinear coordinates is simplicity: many complications arise when coordinates are not orthogonal. For example, in orthogonal coordinates many problems may be solved by separation of variables. Separation of variables is a mathematical technique that converts a complex d-dimensional problem into d one-dimensional problems that can be solved in terms of known functions. Many equations can be reduced to Laplace's equation or the Helmholtz equation. Laplace's equation is separable in 13 orthogonal coordinate systems (the 14 listed in the table below with the exception of toroidal), and the Helmholtz equation is separable in 11 orthogonal coordinate systems.

Orthogonal coordinates never have off-diagonal terms in their metric tensor. In other words, the infinitesimal squared distance ds² can always be written as a scaled sum of the squared infinitesimal coordinate displacements

[math]\displaystyle{ ds^2 = \sum_{k=1}^d \left( h_k \, dq^{k} \right)^2 }[/math]

where d is the dimension and the scaling functions (or scale factors)

[math]\displaystyle{ h_{k}(\mathbf{q})\ \stackrel{\mathrm{def}}{=}\ \sqrt{g_{kk}(\mathbf{q})} = |\mathbf e_k| }[/math]

equal the square roots of the diagonal components of the metric tensor, or the lengths of the local basis vectors [math]\displaystyle{ \mathbf e_k }[/math] described below. These scaling functions h_i are used to calculate differential operators in the new coordinates, e.g., the gradient, the Laplacian, the divergence and the curl.

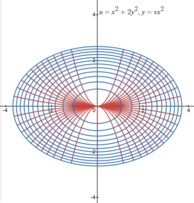
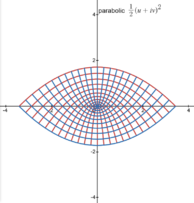
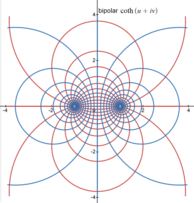
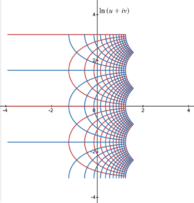
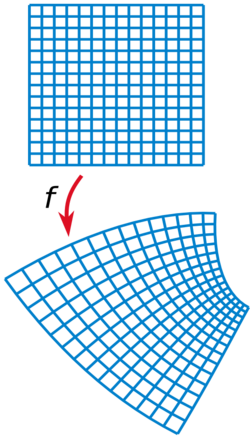
A simple method for generating orthogonal coordinates systems in two dimensions is by a conformal mapping of a standard two-dimensional grid of Cartesian coordinates (x, y). A complex number z = x + iy can be formed from the real coordinates x and y, where i represents the imaginary unit. Any holomorphic function w = f(z) with non-zero complex derivative will produce a conformal mapping; if the resulting complex number is written w = u + iv, then the curves of constant u and v intersect at right angles, just as the original lines of constant x and y did.

Orthogonal coordinates in three and higher dimensions can be generated from an orthogonal two-dimensional coordinate system, either by projecting it into a new dimension (cylindrical coordinates) or by rotating the two-dimensional system about one of its symmetry axes. However, there are other orthogonal coordinate systems in three dimensions that cannot be obtained by projecting or rotating a two-dimensional system, such as the ellipsoidal coordinates. More general orthogonal coordinates may be obtained by starting with some necessary coordinate surfaces and considering their orthogonal trajectories.

Basis vectors

Covariant basis

In Cartesian coordinates, the basis vectors are fixed (constant). In the more general setting of curvilinear coordinates, a point in space is specified by the coordinates, and at every such point there is bound a set of basis vectors, which generally are not constant: this is the essence of curvilinear coordinates in general and is a very important concept. What distinguishes orthogonal coordinates is that, though the basis vectors vary, they are always orthogonal with respect to each other. In other words,

[math]\displaystyle{ \mathbf e_i \cdot \mathbf e_j = 0 \quad \text{if} \quad i \neq j }[/math]

These basis vectors are by definition the tangent vectors of the curves obtained by varying one coordinate, keeping the others fixed:

Visualization of 2D orthogonal coordinates. Curves obtained by holding all but one coordinate constant are shown, along with basis vectors. Note that the basis vectors aren't of equal length: they need not be, they only need to be orthogonal.

[math]\displaystyle{ \mathbf e_i = \frac{\partial \mathbf r}{\partial q^i} }[/math]

where r is some point and qⁱ is the coordinate for which the basis vector is extracted. In other words, a curve is obtained by fixing all but one coordinate; the unfixed coordinate is varied as in a parametric curve, and the derivative of the curve with respect to the parameter (the varying coordinate) is the basis vector for that coordinate.

Note that the vectors are not necessarily of equal length. The useful functions known as scale factors of the coordinates are simply the lengths [math]\displaystyle{ h_i }[/math] of the basis vectors [math]\displaystyle{ \hat{\mathbf e}_i }[/math] (see table below). The scale factors are sometimes called Lamé coefficients, not to be confused with Lamé parameters (solid mechanics).

The normalized basis vectors are notated with a hat and obtained by dividing by the length:

[math]\displaystyle{ \hat{\mathbf e}_i = \frac{{\mathbf e}_i}{h_i} = \frac{{\mathbf e}_i}{\left|{\mathbf e}_i\right|} }[/math]

A vector field may be specified by its components with respect to the basis vectors or the normalized basis vectors, and one must be sure which case is meant. Components in the normalized basis are most common in applications for clarity of the quantities (for example, one may want to deal with tangential velocity instead of tangential velocity times a scale factor); in derivations the normalized basis is less common since it is more complicated.

Contravariant basis

The basis vectors shown above are covariant basis vectors (because they "co-vary" with vectors). In the case of orthogonal coordinates, the contravariant basis vectors are easy to find since they will be in the same direction as the covariant vectors but reciprocal length (for this reason, the two sets of basis vectors are said to be reciprocal with respect to each other):

[math]\displaystyle{ \mathbf e^i = \frac{\hat{\mathbf e}_i}{h_i} = \frac{\mathbf e_i}{h_i^2} }[/math]

this follows from the fact that, by definition, [math]\displaystyle{ \mathbf e_i \cdot \mathbf e^j = \delta^j_i }[/math], using the Kronecker delta. Note that:

[math]\displaystyle{ \hat{\mathbf e}_i = \frac{\mathbf e_i}{h_i} = h_i \mathbf e^i = \hat{\mathbf e}^i }[/math]

We now face three different basis sets commonly used to describe vectors in orthogonal coordinates: the covariant basis e_i, the contravariant basis eⁱ, and the normalized basis êⁱ. While a vector is an objective quantity, meaning its identity is independent of any coordinate system, the components of a vector depend on what basis the vector is represented in.

To avoid confusion, the components of the vector x with respect to the e_i basis are represented as xⁱ, while the components with respect to the eⁱ basis are represented as x_i:

[math]\displaystyle{ \mathbf x = \sum_i x^i \mathbf e_i = \sum_i x_i \mathbf e^i }[/math]

The position of the indices represent how the components are calculated (upper indices should not be confused with exponentiation). Note that the summation symbols Σ (capital Sigma) and the summation range, indicating summation over all basis vectors (i = 1, 2, ..., d), are often omitted. The components are related simply by:

[math]\displaystyle{ h_i^2 x^i = x_i }[/math]

There is no distinguishing widespread notation in use for vector components with respect to the normalized basis; in this article we'll use subscripts for vector components and note that the components are calculated in the normalized basis.

Vector algebra

Vector addition and negation are done component-wise just as in Cartesian coordinates with no complication. Extra considerations may be necessary for other vector operations.

Note however, that all of these operations assume that two vectors in a vector field are bound to the same point (in other words, the tails of vectors coincide). Since basis vectors generally vary in orthogonal coordinates, if two vectors are added whose components are calculated at different points in space, the different basis vectors require consideration.

Dot product

The dot product in Cartesian coordinates (Euclidean space with an orthonormal basis set) is simply the sum of the products of components. In orthogonal coordinates, the dot product of two vectors x and y takes this familiar form when the components of the vectors are calculated in the normalized basis:

[math]\displaystyle{ \mathbf x \cdot \mathbf y = \sum_i x_i \hat{\mathbf e}_i \cdot \sum_j y_j \hat{\mathbf e}_j = \sum_i x_i y_i }[/math]

This is an immediate consequence of the fact that the normalized basis at some point can form a Cartesian coordinate system: the basis set is orthonormal.

For components in the covariant or contravariant bases,

[math]\displaystyle{ \mathbf x \cdot \mathbf y = \sum_i h_i^2 x^i y^i = \sum_i \frac{x_i y_i}{h_i^2} = \sum_i x^i y_i = \sum_i x_i y^i }[/math]

This can be readily derived by writing out the vectors in component form, normalizing the basis vectors, and taking the dot product. For example, in 2D:

[math]\displaystyle{ \begin{align} \mathbf x \cdot \mathbf y & = \left(x^1 \mathbf e_1 + x^2 \mathbf e_2\right) \cdot \left(y_1 \mathbf e^1 + y_2 \mathbf e^2\right) \\[10pt] & = \left(x^1 h_1 \hat{ \mathbf e}_1 + x^2 h_2 \hat{ \mathbf e}_2\right) \cdot \left(y_1 \frac{\hat{ \mathbf e}^1}{h_1} + y_2 \frac{\hat{ \mathbf e}^2}{h_2}\right) = x^1 y_1 + x ^2 y_2 \end{align} }[/math]

where the fact that the normalized covariant and contravariant bases are equal has been used.

Cross product

The cross product in 3D Cartesian coordinates is:

[math]\displaystyle{ \mathbf x \times \mathbf y = (x_2 y_3 - x_3 y_2) \hat{ \mathbf e}_1 + (x_3 y_1 - x_1 y_3) \hat{ \mathbf e}_2 + (x_1 y_2 - x_2 y_1) \hat{ \mathbf e}_3 }[/math]

The above formula then remains valid in orthogonal coordinates if the components are calculated in the normalized basis.

To construct the cross product in orthogonal coordinates with covariant or contravariant bases we again must simply normalize the basis vectors, for example:

[math]\displaystyle{ \mathbf x \times \mathbf y = \sum_i x^i \mathbf e_i \times \sum_j y^j \mathbf e_j = \sum_i x^i h_i \hat{\mathbf e}_i \times \sum_j y^j h_j \hat{\mathbf e}_j }[/math]

which, written expanded out,

[math]\displaystyle{ \mathbf x \times \mathbf y = \left(x^2 y^3 - x^3 y^2\right) \frac{h_2 h_3}{h_1} \mathbf e_1 + \left(x^3 y^1 - x^1 y^3\right) \frac{h_1 h_3}{h_2} \mathbf e_2 + \left(x^1 y^2 - x^2 y^1\right) \frac{h_1 h_2}{h_3} \mathbf e_3 }[/math]

Terse notation for the cross product, which simplifies generalization to non-orthogonal coordinates and higher dimensions, is possible with the Levi-Civita tensor, which will have components other than zeros and ones if the scale factors are not all equal to one.

Vector calculus

Differentiation

Looking at an infinitesimal displacement from some point, it's apparent that

[math]\displaystyle{ d\mathbf r = \sum_i \frac{\partial \mathbf r}{\partial q^i} \, dq^i = \sum_i \mathbf e_i \, dq^i }[/math]

By definition, the gradient of a function must satisfy (this definition remains true if ƒ is any tensor)

[math]\displaystyle{ df = \nabla f \cdot d\mathbf r \quad \Rightarrow \quad df = \nabla f \cdot \sum_i \mathbf e_i \, dq^i }[/math]

It follows then that del operator must be:

[math]\displaystyle{ \nabla = \sum_i \mathbf e^i \frac{\partial}{\partial q^i} }[/math]

and this happens to remain true in general curvilinear coordinates. Quantities like the gradient and Laplacian follow through proper application of this operator.

Basis vector formulae

From dr and normalized basis vectors ê_i, the following can be constructed.

Differential element	Vectors	Scalars
Line element	Tangent vector to coordinate curve qi: [math]\displaystyle{ d\boldsymbol{\ell} = h_i dq^i \hat{\mathbf{e}}_i = \frac{\partial \mathbf{r}}{\partial q^i} dq^i }[/math]	Infinitesimal length [math]\displaystyle{ d\ell = \sqrt{d\mathbf{r}\cdot d\mathbf{r}} = \sqrt{(h_1 \, dq^1)^2 + (h_2 \, dq^2)^2 + (h_3 \, dq^3)^2} }[/math]
Surface element	Normal to coordinate surface qk = constant: [math]\displaystyle{ \begin{align} d\mathbf{S} & = (h_i dq^i \hat{\mathbf{e}}_i) \times (h_j dq^j \hat{\mathbf{e}}_j) \\ & = dq^i dq^j \left(\frac{\partial \mathbf{r}}{\partial q^i} \times \frac{\partial \mathbf{r}}{\partial q^j}\right)\\ & = h_i h_j dq^i dq^j \hat{\mathbf{e}}_k \end{align} }[/math]	Infinitesimal surface [math]\displaystyle{ dS_k = h_ih_j \, dq^i \, dq^j }[/math]
Volume element	N/A	Infinitesimal volume [math]\displaystyle{ \begin{align} dV & = |(h_1 \, dq^1 \hat{\mathbf{e}}_1) \cdot (h_2 \, dq^2 \hat{\mathbf{e}}_2) \times (h_3 \, dq^3 \hat{\mathbf{e}}_3)| \\ & = |\hat{\mathbf{e}}_1 \cdot \hat{\mathbf{e}}_2 \times \hat{\mathbf{e}}_3| h_1 h_2 h_3 \, dq^1 \, dq^2 \, dq^3\\ & = h_1 h_2 h_3 \, dq^1 \, dq^2 \, dq^3 \\ & = J \, dq^1 \, dq^2 \, dq^3 \end{align} }[/math]

where

[math]\displaystyle{ J = \left|\frac{\partial\mathbf{r}}{\partial q^1} \cdot \left(\frac{\partial\mathbf{r}}{\partial q^2} \times \frac{\partial\mathbf{r}}{\partial q^3} \right)\right| = \left|\frac{\partial(x, y, z)}{\partial(q^1, q^2, q^3)} \right| = h_1 h_2 h_3 }[/math]

is the Jacobian determinant, which has the geometric interpretation of the deformation in volume from the infinitesimal cube dxdydz to the infinitesimal curved volume in the orthogonal coordinates.

Integration

Using the line element shown above, the line integral along a path [math]\displaystyle{ \scriptstyle \mathcal P }[/math] of a vector F is:

[math]\displaystyle{ \int_{\mathcal P} \mathbf F \cdot d\mathbf r = \int_{\mathcal P} \sum_i F_i \mathbf e^i \cdot \sum_j \mathbf e_j \, dq^j = \sum_i \int_{\mathcal P} F_i \, dq^i }[/math]

An infinitesimal element of area for a surface described by holding one coordinate q_k constant is:

[math]\displaystyle{ dA_k = \prod_{i \neq k} ds_i = \prod_{i \neq k} h_i \, dq^i }[/math]

Similarly, the volume element is:

[math]\displaystyle{ dV = \prod_i ds_i = \prod_i h_i \, dq^i }[/math]

where the large symbol Π (capital Pi) indicates a product the same way that a large Σ indicates summation. Note that the product of all the scale factors is the Jacobian determinant.

As an example, the surface integral of a vector function F over a q¹ = constant surface [math]\displaystyle{ \scriptstyle\mathcal S }[/math] in 3D is:

[math]\displaystyle{ \int_{\mathcal S} \mathbf F \cdot d\mathbf A = \int_{\mathcal S} \mathbf F \cdot \hat{\mathbf n} \ d A = \int_{\mathcal S} \mathbf F \cdot \hat{\mathbf e}_1 \ d A = \int_{\mathcal S} F^1 \frac{h_2 h_3}{h_1} \, dq^2 \, dq^3 }[/math]

Note that F¹/h₁ is the component of F normal to the surface.

Differential operators in three dimensions

Since these operations are common in application, all vector components in this section are presented with respect to the normalised basis: [math]\displaystyle{ F_i = \mathbf{F} \cdot \hat{\mathbf{e}}_i }[/math].

Operator	Expression
Gradient of a scalar field	[math]\displaystyle{ \nabla \phi = \frac{\hat{ \mathbf e}_1}{h_1} \frac{\partial \phi}{\partial q^1} + \frac{\hat{ \mathbf e}_2}{h_2} \frac{\partial \phi}{\partial q^2} + \frac{\hat{ \mathbf e}_3}{h_3} \frac{\partial \phi}{\partial q^3} }[/math]
Divergence of a vector field	[math]\displaystyle{ \nabla \cdot \mathbf F = \frac{1}{h_1 h_2 h_3} \left[ \frac{\partial}{\partial q^1} \left( F_1 h_2 h_3 \right) + \frac{\partial}{\partial q^2} \left( F_2 h_3 h_1 \right) + \frac{\partial}{\partial q^3} \left( F_3 h_1 h_2 \right) \right] }[/math]
Curl of a vector field	[math]\displaystyle{ \begin{align} \nabla \times \mathbf F & = \frac{\hat{ \mathbf e}_1}{h_2 h_3} \left[ \frac{\partial}{\partial q^2} \left( h_3 F_3 \right) - \frac{\partial}{\partial q^3} \left( h_2 F_2 \right) \right] + \frac{\hat{ \mathbf e}_2}{h_3 h_1} \left[ \frac{\partial}{\partial q^3} \left( h_1 F_1 \right) - \frac{\partial}{\partial q^1} \left( h_3 F_3 \right) \right] \\[10pt] & + \frac{\hat{ \mathbf e}_3}{h_1 h_2} \left[ \frac{\partial}{\partial q^1} \left( h_2 F_2 \right) - \frac{\partial}{\partial q^2} \left( h_1 F_1 \right) \right] =\frac{1}{h_1 h_2 h_3} \begin{vmatrix} h_1\hat{\mathbf{e}}_1 & h_2\hat{\mathbf{e}}_2 & h_3\hat{\mathbf{e}}_3 \\ \dfrac{\partial}{\partial q^1} & \dfrac{\partial}{\partial q^2} & \dfrac{\partial}{\partial q^3} \\ h_1 F_1 & h_2 F_2 & h_3 F_3 \end{vmatrix} \end{align} }[/math]
Laplacian of a scalar field	[math]\displaystyle{ \nabla^2 \phi = \frac{1}{h_1 h_2 h_3} \left[ \frac{\partial}{\partial q^1} \left( \frac{h_2 h_3}{h_1} \frac{\partial \phi}{\partial q^1} \right) + \frac{\partial}{\partial q^2} \left( \frac{h_3 h_1}{h_2} \frac{\partial \phi}{\partial q^2} \right) + \frac{\partial}{\partial q^3} \left( \frac{h_1 h_2}{h_3} \frac{\partial \phi}{\partial q^3} \right) \right] }[/math]

The above expressions can be written in a more compact form using the Levi-Civita symbol [math]\displaystyle{ \epsilon_{ijk} }[/math] and the Jacobian determinant [math]\displaystyle{ J = h_1 h_2 h_3 }[/math], assuming summation over repeated indices:

Operator	Expression
Gradient of a scalar field	[math]\displaystyle{ \nabla \phi = \frac{\hat{ \mathbf e}_k}{h_k} \frac{\partial \phi}{\partial q^k} }[/math]
Divergence of a vector field	[math]\displaystyle{ \nabla \cdot \mathbf F = \frac{1}{J}\frac{\partial}{\partial q^k} \left(\frac{J}{h_k} F_k\right) }[/math]
Curl of a vector field (3D only)	[math]\displaystyle{ \nabla \times \mathbf F = \frac{h_k \hat{ \mathbf e}_k}{J} \epsilon_{ijk}\frac{\partial}{\partial q^i}\left(h_j F_j\right) }[/math]
Laplacian of a scalar field	[math]\displaystyle{ \nabla^2 \phi = \frac{1}{J} \frac{\partial}{\partial q^k}\left(\frac{J}{h_k^2}\frac{\partial \phi}{\partial q^k}\right) }[/math]

Also notice the gradient of a scalar field can be expressed in terms of the Jacobian matrix J containing canonical partial derivatives:

[math]\displaystyle{ \mathbf{J} = \left[\frac{\partial \phi}{\partial q^1}, \frac{\partial \phi}{\partial q^2}, \frac{\partial \phi}{\partial q^3}\right] }[/math]

upon a change of basis:

[math]\displaystyle{ \nabla \phi = \mathbf{S} \mathbf{R} \mathbf{J}^T }[/math]

where the rotation and scaling matrices are:

[math]\displaystyle{ \mathbf{R} = [\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3] }[/math]

[math]\displaystyle{ \mathbf{S} = \mathrm{diag}([h_1^{-1}, h_2^{-1}, h_3^{-1}]). }[/math]

Table of two-dimensional orthogonal coordinates

System	Complex Transform [math]\displaystyle{ x+iy = f(u+iv) }[/math]	Shape of [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] isolines	Comment
Cartesian	[math]\displaystyle{ u + iv }[/math]	line, line
Log-polar	[math]\displaystyle{ \exp(u+iv) }[/math]	circle, line	for [math]\displaystyle{ u = \ln r }[/math] becomes Polar
Parabolic	[math]\displaystyle{ \frac12 (u+iv)^2 }[/math]	parabola, parabola
point dipol	[math]\displaystyle{ (u+iv)^{-1} }[/math]	circle, circle
Elliptic	[math]\displaystyle{ \cosh(u+iv) }[/math]	ellipse, hyperbola	field of a needle, appears Log-polar for large distances
Bipolar	[math]\displaystyle{ \coth(u+iv) }[/math]	circle, circle	appears like point dipol for large distances
	[math]\displaystyle{ \sqrt{u+iv} }[/math]	hyperbola, hyperbola	field of a inner edge
	[math]\displaystyle{ u = x^2 + 2y^2,\ y=vx^2 }[/math]	elipse, parabola

cartesian

polar

logpolar

ellipse parabola

parabolic

point dipol

sqrt(u+iv)

elliptic

bipolar

inverse logpolar

Examples of two-dimensional orthogonal coordinates (https://www.desmos.com/calculator/m5gmtg4n1d).

Table of three-dimensional orthogonal coordinates

Besides the usual cartesian coordinates, several others are tabulated below. Interval notation is used for compactness in the coordinates column, and the entries are grouped by their interval signatures, e.g. COCCCO for spherical coordinates. The entries are not sorted by their interval signatures in alphabetic order. After the grouping of the entries by interval signature, the sort order here is alphabetic by the curvilinear coordinate system name.

Curvillinear coordinates (q1, q2, q3)	Transformation from cartesian (x, y, z)	Scale factors
Spherical coordinates [math]\displaystyle{ (r, \theta, \phi)\in[0,\infty)\times[0,\pi]\times[0,2\pi) }[/math]	[math]\displaystyle{ \begin{align} x&=r\sin\theta\cos\phi \\ y&=r\sin\theta\sin\phi \\ z&=r\cos\theta \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=1 \\ h_2&=r \\ h_3&=r\sin\theta \end{align} }[/math]
Parabolic coordinates [math]\displaystyle{ (u, v, \phi)\in[0,\infty)\times[0,\infty)\times[0,2\pi) }[/math]	[math]\displaystyle{ \begin{align} x&=uv\cos\phi\\ y&=uv\sin\phi\\ z&=\frac{1}{2}(u^2-v^2) \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=\sqrt{u^2+v^2} \\ h_3&=uv \end{align} }[/math]
Bipolar cylindrical coordinates [math]\displaystyle{ (u,v,z)\in[0,2\pi)\times(-\infty,\infty)\times(-\infty,\infty) }[/math]	[math]\displaystyle{ \begin{align} x&=\frac{a\sinh v}{\cosh v - \cos u}\\ y&=\frac{a\sin u}{\cosh v - \cos u}\\ z&=z \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=\frac{a}{\cosh v - \cos u}\\ h_3&=1 \end{align} }[/math]
Ellipsoidal coordinates [math]\displaystyle{ \begin{align} & (\lambda, \mu, \nu)\in[0, c^2)\times(c^2, b^2)\times(b^2, a^2)\\ & \lambda \lt c^2 \lt b^2 \lt a^2,\\ & c^2 \lt \mu \lt b^2 \lt a^2,\\ & c^2 \lt b^2 \lt \nu \lt a^2, \end{align} }[/math]	[math]\displaystyle{ \frac{x^2}{a^2 - q_i} + \frac{y^2}{b^2 - q_i} + \frac{z^2}{c^2 - q_i} = 1 }[/math] where [math]\displaystyle{ (q_1,q_2,q_3)=(\lambda,\mu,\nu) }[/math]	[math]\displaystyle{ h_i=\frac{1}{2} \sqrt{\frac{(q_j-q_i)(q_k-q_i)}{(a^2-q_i)(b^2-q_i)(c^2-q_i)}} }[/math]
Paraboloidal coordinates [math]\displaystyle{ \begin{align} & (\lambda, \mu, \nu)\in[0,b^2)\times(b^2,a^2)\times(a^2,\infty)\\ & b^2 \lt a^2 \end{align} }[/math]	[math]\displaystyle{ \frac{x^2}{q_i - a^2} + \frac{y^2}{q_i - b^2} = 2 z + q_i }[/math] where [math]\displaystyle{ (q_1,q_2,q_3)=(\lambda,\mu,\nu) }[/math]	[math]\displaystyle{ h_i=\frac{1}{2} \sqrt{\frac{(q_j-q_i)(q_k-q_i)}{(a^2-q_i)(b^2-q_i)}} }[/math]
Cylindrical polar coordinates [math]\displaystyle{ (r, \phi, z)\in[0,\infty)\times[0,2\pi)\times(-\infty,\infty) }[/math]	[math]\displaystyle{ \begin{align} x&=r\cos\phi \\ y&=r\sin\phi \\ z&=z \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_3=1 \\ h_2&=r \end{align} }[/math]
Elliptic cylindrical coordinates [math]\displaystyle{ (u, v, z)\in[0,\infty)\times[0,2\pi)\times(-\infty,\infty) }[/math]	[math]\displaystyle{ \begin{align} x&=a\cosh u \cos v\\ y&=a\sinh u \sin v\\ z&=z \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=a\sqrt{\sinh^2u+\sin^2v} \\ h_3&=1 \end{align} }[/math]
Oblate spheroidal coordinates [math]\displaystyle{ (\xi, \eta, \phi)\in[0,\infty)\times\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\times[0,2\pi) }[/math]	[math]\displaystyle{ \begin{align} x&=a\cosh\xi\cos\eta\cos\phi\\ y&=a\cosh\xi\cos\eta\sin\phi\\ z&=a\sinh\xi\sin\eta \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=a\sqrt{\sinh^2\xi+\sin^2\eta} \\ h_3&=a\cosh\xi\cos\eta \end{align} }[/math]
Prolate spheroidal coordinates [math]\displaystyle{ (\xi, \eta, \phi)\in[0,\infty)\times[0,\pi]\times[0,2\pi) }[/math]	[math]\displaystyle{ \begin{align} x&=a\sinh\xi\sin\eta\cos\phi\\ y&=a\sinh\xi\sin\eta\sin\phi\\ z&=a\cosh\xi\cos\eta \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=a\sqrt{\sinh^2\xi+\sin^2\eta} \\ h_3&=a\sinh\xi\sin\eta \end{align} }[/math]
Bispherical coordinates [math]\displaystyle{ (u,v,\phi)\in(-\pi,\pi]\times[0,\infty)\times[0,2\pi) }[/math]	[math]\displaystyle{ \begin{align} x &= \frac{a\sin u \cos \phi}{\cosh v - \cos u}\\ y &= \frac{a\sin u \sin \phi}{\cosh v - \cos u} \\ z &= \frac{a\sinh v}{\cosh v - \cos u} \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=\frac{a}{\cosh v - \cos u}\\ h_3&=\frac{a\sin u}{\cosh v - \cos u} \end{align} }[/math]
Toroidal coordinates [math]\displaystyle{ (u,v,\phi)\in(-\pi,\pi]\times[0,\infty)\times[0,2\pi) }[/math]	[math]\displaystyle{ \begin{align} x &= \frac{a\sinh v \cos\phi}{\cosh v - \cos u}\\ y &= \frac{a\sinh v \sin\phi}{\cosh v - \cos u} \\ z &= \frac{a\sin u}{\cosh v - \cos u} \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=\frac{a}{\cosh v - \cos u}\\ h_3&=\frac{a\sinh v}{\cosh v - \cos u} \end{align} }[/math]
Parabolic cylindrical coordinates [math]\displaystyle{ (u, v, z)\in(-\infty,\infty)\times[0,\infty)\times(-\infty,\infty) }[/math]	[math]\displaystyle{ \begin{align} x&=\frac{1}{2}(u^2-v^2)\\ y&=uv\\ z&=z \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=h_2=\sqrt{u^2+v^2} \\ h_3&=1 \end{align} }[/math]
Conical coordinates [math]\displaystyle{ \begin{align} & (\lambda,\mu,\nu)\\ & \nu^2 \lt b^2 \lt \mu^2 \lt a^2 \\ & \lambda \in [0,\infty) \end{align} }[/math]	[math]\displaystyle{ \begin{align} x &= \frac{\lambda\mu\nu}{ab}\\ y &= \frac{\lambda}{a}\sqrt{\frac{(\mu^2-a^2)(\nu^2-a^2)}{a^2-b^2}} \\ z &= \frac{\lambda}{b}\sqrt{\frac{(\mu^2-b^2)(\nu^2-b^2)}{b^2-a^2}} \end{align} }[/math]	[math]\displaystyle{ \begin{align} h_1&=1\\ h_2^2&=\frac{\lambda^2(\mu^2-\nu^2)}{(\mu^2-a^2)(b^2-\mu^2)}\\ h_3^2&=\frac{\lambda^2(\mu^2-\nu^2)}{(\nu^2-a^2)(\nu^2-b^2)} \end{align} }[/math]

See also

• Curvilinear coordinates
• Geodetic coordinates
• Tensor
• Vector field
• Skew coordinates

References

• Korn GA and Korn TM. (1961) Mathematical Handbook for Scientists and Engineers, McGraw-Hill, pp. 164–182.
• Morse and Feshbach (1953). Methods of Theoretical Physics, Volume 1. McGraw-Hill. 

• Margenau H. and Murphy GM. (1956) The Mathematics of Physics and Chemistry, 2nd. ed., Van Nostrand, pp. 172–192.
• Leonid P. Lebedev and Michael J. Cloud (2003) Tensor Analysis, pp. 81 – 88.