De divina proportione

From HandWiki
De divina proportione
Title page of De divina proportione
Title page of 1509 edition
AuthorLuca Pacioli
IllustratorLeonardo da Vinci
CountryRepublic of Venice
LanguageItalian
SubjectGeometry, Architecture
PublisherPaganini (Venice)
Publication date
1509

De divina proportione (On the Divine Proportion) is a book on mathematics written by Luca Pacioli and illustrated by Leonardo da Vinci, composed around 1498 in Milan and first printed in 1509.[1] Its subject was mathematical proportions (the title refers to the golden ratio) and their applications to geometry, visual art through perspective, and architecture. The clarity of the written material and Leonardo's excellent diagrams helped the book to achieve an impact beyond mathematical circles, popularizing contemporary geometric concepts and images.[2][3]

Contents of the book

Further information: Mathematics and art
Woodcut illustrating proportions of the human face. Note that despite the label in the image, the lines drawn relate to Vitruvius' system of integers and do not correspond in any way to the golden ratio.

The book consists of three separate manuscripts,[1] which Pacioli worked on between 1496 and 1498.

Compendio divina proportione

The first part, Compendio divina proportione (Compendium on the Divine Proportion), studies the golden ratio from a mathematical perspective (following the relevant work of Euclid) and explores its applications to various arts, in seventy-one chapters.[1] It also contains a discourse on the regular and semiregular polyhedra,[4][5] as well as a discussion of the use of geometric perspective by painters such as Piero della Francesca, Melozzo da Forlì and Marco Palmezzano.

Trattato dell'architettura

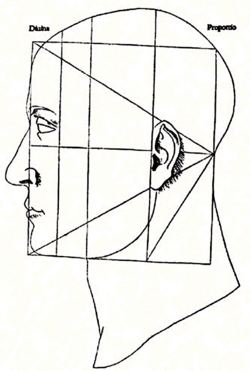
The second part, Trattato dell'architettura (Treatise on Architecture), discusses the ideas of Vitruvius (from his De architectura) on the application of mathematics to architecture in twenty chapters. The text compares the proportions of the human body to those of artificial structures, with examples from classical Greco-Roman architecture.

Libellus in tres partiales divisus

The third part, Libellus in tres partiales divisus (Book divided into three parts), is mainly an Italian translation of Piero della Francesca's Latin writings On [the] Five Regular Solids ("De quinque corporibus regularibus")[1] and mathematical examples.[4] In 1550 Giorgio Vasari wrote a biography of della Francesca, in which he accused Pacioli of plagiarism and claimed that he stole della Francesca's work on perspective, on arithmetic and on geometry.[1]

Illustrations

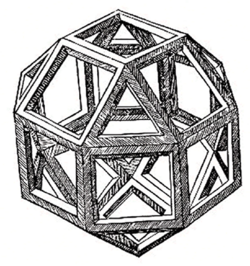
The first printed illustration of a rhombicuboctahedron, by Leonardo da Vinci.

After these three parts are appended two sections of illustrations, the first showing twenty-three capital letters drawn with a ruler and compass by Pacioli and the second with some sixty illustrations in woodcut after drawings by Leonardo da Vinci.[6] Leonardo drew the illustrations of the regular solids while he lived with and took mathematics lessons from Pacioli. Leonardo's drawings are probably the first illustrations of skeletonic solids which allowed an easy distinction between front and back.

History

Pacioli produced three manuscripts of the treatise by different scribes. He gave the first copy with a dedication to the Duke of Milan, Ludovico il Moro; this manuscript is now preserved in Switzerland at the Bibliothèque de Genève in Geneva. A second copy was donated to Galeazzo da Sanseverino and now rests at the Biblioteca Ambrosiana in Milan. The third, which has gone missing, was given to Pier Soderini, the Gonfaloniere of Florence.[7] On 1 June 1509 the first printed edition was published in Venice by Paganino Paganini;[8] it has since been reprinted several times.

Architectural letter 'M'

The book was displayed as part of an exhibition in Milan between October 2005 and October 2006 together with the Codex Atlanticus.[9] The "M" logo used by the Metropolitan Museum of Art in New York is adapted from one in De divina proportione.[10]

See also

  • Frederik Macody Lund
  • Samuel Colman

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 O'Connor, J J; Robertson, E F (July 1999). "Luca Pacioli". University of St Andrews. http://www-history.mcs.st-and.ac.uk/Biographies/Pacioli.html. Retrieved 15 January 2015. 
  2. ↑ Hart, George W.. "Luca Pacioli's Polyhedra". http://www.georgehart.com/virtual-polyhedra/pacioli.html. Retrieved 23 January 2015. 
  3. ↑ Hoechsmann, Klaus Hoechsmann (1 April 2001). "The Rose and the Nautilus". University of British Columbia. http://www.math.ubc.ca/~hoek/Teaching/Golden/Divina.html. Retrieved 15 January 2015. 
  4. ↑ 4.0 4.1 Gardes, Michel (20 June 2001). "La Divine Proportion de Luca Pacioli" (in French). Académie de Poitiers. Archived from the original on 27 January 2015. https://web.archive.org/web/20150127090823/http://ww3.ac-poitiers.fr/arts_p/b%40lise14/pageshtm/page_4.htm. Retrieved 15 January 2015. 
  5. ↑ Field, J F (1997). "Rediscovering the Archimedean polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler". Arch. Hist. Exact Sci. 50 (3-4): 241–289. 
  6. ↑ "Divina proportione, after Leonardo da Vinci". Metropolitan Museum of Art, New York. http://www.metmuseum.org/works_of_art/collection_database/drawings_and_prints/divina_proportione_leonardo_da_vinci/objectview.aspx?collID=9&OID=90003660. Retrieved 15 January 2015. 
  7. ↑ Di Teodoro, Francesco Paolo (2014). "PACIOLI, Luca" (in Italian). Dizionario Biografico degli Italiani. 80. Treccani. http://www.treccani.it/enciclopedia/luca-pacioli_%28Dizionario-Biografico%29/. Retrieved 30 January 2015. 
  8. ↑ Nuovo, Angela (2014). "PAGANINI, Paganino" (in Italian). Dizionario Biografico degli Italiani. 80. Treccani. http://www.treccani.it/enciclopedia/paganino-paganini_%28Dizionario-Biografico%29/. Retrieved 27 January 2015. 
  9. ↑ "The Virtual Codex Atlanticus". https://www.leonardo3.net/leonardo/atlantico/manoscritti_eng.htm. Retrieved 15 January 2015. 
  10. ↑ "Renaissance 'M' Bookmark". Metropolitan Museum of Art, New York. http://store.metmuseum.org/magnets-bookmarks+novelties/renaissance-m-bookmark/invt/10086668/. Retrieved 15 January 2015. 

External links




Retrieved from "https://handwiki.org/wiki/index.php?title=De_divina_proportione&oldid=2453709"