Mathematical beauty
Mathematical beauty is the aesthetic pleasure derived from the abstractness, purity, simplicity, depth or orderliness of mathematics. Mathematicians may express this pleasure by describing mathematics (or, at least, some aspect of mathematics) as beautiful or describe mathematics as an art form, (a position taken by G. H. Hardy[1]) or, at a minimum, as a creative activity.
Comparisons are made with music and poetry.
In method
Mathematicians[who?][when?] describe an especially pleasing method of proof as elegant. Depending on context, this may mean:
- A proof that uses a minimum of additional assumptions or previous results.
- A proof that is unusually succinct.
- A proof that derives a result in a surprising way (e.g., from an apparently unrelated theorem or a collection of theorems).
- A proof that is based on new and original insights.
- A method of proof that can be easily generalized to solve a family of similar problems.
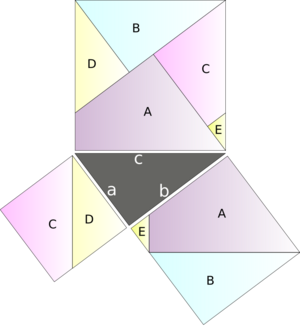
In the search for an elegant proof, mathematicians[who?] oftenTemplate:How often look for different independent ways to prove a result—as the first proof that is found can often be improved. The theorem for which the greatest number of different proofs have been discovered is possibly the Pythagorean theorem, with hundreds of proofs being published up to date.[2] Another theorem that has been proved in many different ways is the theorem of quadratic reciprocity. In fact, Carl Friedrich Gauss alone had eight different proofs of this theorem, six of which he published.[3]
Conversely, results that are logically correct but involve laborious calculations, over-elaborate methods, highly conventional approaches or a large number of powerful axioms or previous results are usually not considered to be elegant, and may be even referred to as ugly or clumsy.
In results
Some mathematicians see beauty in mathematical results that establish connections between two areas of mathematics that at first sight appear to be unrelated.[4] These results are often described as deep. While it is difficult to find universal agreement on whether a result is deep, some examples are more commonly cited than others. One such example is Euler's identity:[5]
[math]\displaystyle{ \displaystyle e^{i \pi} +1 = 0\, . }[/math]
This elegant expression ties together arguably the five most important mathematical constants (e, i, π, 1, and 0) with the two most common mathematical symbols (+, =). Euler's identity is a special case of Euler's formula, which the physicist Richard Feynman called "our jewel" and "the most remarkable formula in mathematics".[6] Modern examples include the modularity theorem, which establishes an important connection between elliptic curves and modular forms (work on which led to the awarding of the Wolf Prize to Andrew Wiles and Robert Langlands), and "monstrous moonshine", which connects the Monster group to modular functions via string theory (for which Richard Borcherds was awarded the Fields Medal).
Other examples of deep results include unexpected insights into mathematical structures. For example, Gauss's Theorema Egregium is a deep theorem which relates a local phenomenon (curvature) to a global phenomenon (area) in a surprising way. In particular, the area of a triangle on a curved surface is proportional to the excess of the triangle and the proportionality is curvature. Another example is the fundamental theorem of calculus[7] (and its vector versions including Green's theorem and Stokes' theorem).
The opposite of deep is trivial. A trivial theorem may be a result that can be derived in an obvious and straightforward way from other known results, or which applies only to a specific set of particular objects such as the empty set. In some occasions, however, a statement of a theorem can be original enough to be considered deep—even though its proof is fairly obvious.
In his 1940 essay A Mathematician's Apology, G. H. Hardy suggested that a beautiful proof or result possesses "inevitability", "unexpectedness", and "economy".[8]
In 1997, Gian-Carlo Rota, disagreed with unexpectedness as a sufficient condition for beauty and proposed a counterexample:
A great many theorems of mathematics, when first published, appear to be surprising; thus for example some twenty years ago [from 1977] the proof of the existence of non-equivalent differentiable structures on spheres of high dimension was thought to be surprising, but it did not occur to anyone to call such a fact beautiful, then or now.[9]
In contrast, Monastyrsky wrote in 2001:
It is very difficult to find an analogous invention in the past to Milnor's beautiful construction of the different differential structures on the seven-dimensional sphere... The original proof of Milnor was not very constructive, but later E. Briscorn showed that these differential structures can be described in an extremely explicit and beautiful form.[10]
This disagreement illustrates both the subjective nature of mathematical beauty and its connection with mathematical results: in this case, not only the existence of exotic spheres, but also a particular realization of them.
In experience
Interest in pure mathematics that is separate from empirical study has been part of the experience of various civilizations, including that of the ancient Greeks, who "did mathematics for the beauty of it".[11] The aesthetic pleasure that mathematical physicists tend to experience in Einstein's theory of general relativity has been attributed (by Paul Dirac, among others) to its "great mathematical beauty".[12] The beauty of mathematics is experienced when the physical reality of objects are represented by mathematical models. Group theory, developed in the early 1800s for the sole purpose of solving polynomial equations, became a fruitful way of categorizing elementary particles—the building blocks of matter. Similarly, the study of knots provides important insights into string theory and loop quantum gravity.[citation needed]
Some[who?] believe that in order to appreciate mathematics, one must engage in doing mathematics.[13]
For example, Math Circles are after-school enrichment programs where students engage with mathematics through lectures and activities; there are also some teachers who encourage student engagement by teaching mathematics in kinesthetic learning. In a general Math Circle lesson, students use pattern finding, observation, and exploration to make their own mathematical discoveries. For example, mathematical beauty arises in a Math Circle activity on symmetry designed for 2nd and 3rd graders, where students create their own snowflakes by folding a square piece of paper and cutting out designs of their choice along the edges of the folded paper. When the paper is unfolded, a symmetrical design reveals itself. In a day to day elementary school mathematics class, symmetry can be presented as such in an artistic manner where students see aesthetically pleasing results in mathematics.[citation needed]
Some[who?] teachers prefer to use mathematical manipulatives to present mathematics in an aesthetically pleasing way. Examples of a manipulative include algebra tiles, cuisenaire rods, and pattern blocks. For example, one can teach the method of completing the square by using algebra tiles. Cuisenaire rods can be used to teach fractions, and pattern blocks can be used to teach geometry. Using mathematical manipulatives helps students gain a conceptual understanding that might not be seen immediately in written mathematical formulas.[14]
Another example of beauty in experience involves the use of origami. Origami, the art of paper folding, has aesthetic qualities and many mathematical connections. One can study the mathematics of paper folding by observing the crease pattern on unfolded origami pieces.[15]
Combinatorics, the study of counting, has artistic representations which some[who?] find mathematically beautiful. There are many visual examples which illustrate combinatorial concepts. Some of the topics and objects seen in combinatorics courses with visual representations include, among others Four color theorem, Young tableau, Permutohedron, Graph theory, Partition of a set.[16]
Brain imaging experiments conducted by Semir Zeki and his colleagues[17] show that the experience of mathematical beauty has, as a neural correlate, activity in field A1 of the medial orbito-frontal cortex (mOFC) of the brain and that this activity is parametrically related to the declared intensity of beauty. The location of the activity is similar to the location of the activity that correlates with the experience of beauty from other sources, such as music or joy or sorrow. Moreover, mathematicians seem resistant to revising their judgment of the beauty of a mathematical formula in light of contradictory opinion given by their peers.[18]
In philosophy
Some[who?] mathematicians are of the opinion that the doing of mathematics is closer to discovery than invention, for example:
There is no scientific discoverer, no poet, no painter, no musician, who will not tell you that he found ready made his discovery or poem or picture—that it came to him from outside, and that he did not consciously create it from within.—William Kingdon Clifford, from a lecture to the Royal Institution titled "Some of the conditions of mental development"
These mathematicians believe that the detailed and precise results of mathematics may be reasonably taken to be true without any dependence on the universe in which we live. For example, they would argue that the theory of the natural numbers is fundamentally valid, in a way that does not require any specific context. Some mathematicians have extrapolated this viewpoint that mathematical beauty is truth further, in some cases becoming mysticism.
In Plato's philosophy there were two worlds, the physical one in which we live and another abstract world which contained unchanging truth, including mathematics. He believed that the physical world was a mere reflection of the more perfect abstract world.[19]
Hungarian mathematician Paul Erdős[20] spoke of an imaginary book, in which God has written down all the most beautiful mathematical proofs. When Erdős wanted to express particular appreciation of a proof, he would exclaim "This one's from The Book!"
Twentieth-century French philosopher Alain Badiou claimed that ontology is mathematics.[21] Badiou also believes in deep connections between mathematics, poetry and philosophy.
In many cases, however, natural philosophers and other scientists who have made extensive use of mathematics have made leaps of inference between beauty and physical truth in ways that turned out to be erroneous. For example, at one stage in his life, Johannes Kepler believed that the proportions of the orbits of the then-known planets in the Solar System have been arranged by God to correspond to a concentric arrangement of the five Platonic solids, each orbit lying on the circumsphere of one polyhedron and the insphere of another. As there are exactly five Platonic solids, Kepler's hypothesis could only accommodate six planetary orbits and was disproved by the subsequent discovery of Uranus.
In information theory
In the 1970s, Abraham Moles and Frieder Nake analyzed links between beauty, information processing, and information theory.[22][23] In the 1990s, Jürgen Schmidhuber formulated a mathematical theory of observer-dependent subjective beauty based on algorithmic information theory: the most beautiful objects among subjectively comparable objects have short algorithmic descriptions (i.e., Kolmogorov complexity) relative to what the observer already knows.[24][25][26] Schmidhuber explicitly distinguishes between beautiful and interesting. The latter corresponds to the first derivative of subjectively perceived beauty: the observer continually tries to improve the predictability and compressibility of the observations by discovering regularities such as repetitions and symmetries and fractal self-similarity. Whenever the observer's learning process (possibly a predictive artificial neural network) leads to improved data compression such that the observation sequence can be described by fewer bits than before, the temporary interesting-ness of the data corresponds to the compression progress, and is proportional to the observer's internal curiosity reward.[27][28]
In the arts
Music
Examples of the use of mathematics in music include the stochastic music of Iannis Xenakis, the Fibonacci sequence in Tool's Lateralus, counterpoint of Johann Sebastian Bach, polyrhythmic structures (as in Igor Stravinsky's The Rite of Spring), the Metric modulation of Elliott Carter, permutation theory in serialism beginning with Arnold Schoenberg, and application of Shepard tones in Karlheinz Stockhausen's Hymnen. They also include the application of Group theory to transformations in music in the theoretical writings of David Lewin.
Visual arts
Examples of the use of mathematics in the visual arts include applications of chaos theory and fractal geometry to computer-generated art, symmetry studies of Leonardo da Vinci, projective geometries in development of the perspective theory of Renaissance art, grids in Op art, optical geometry in the camera obscura of Giambattista della Porta, and multiple perspective in analytic cubism and futurism.
Sacred geometry is a field of its own, giving rise to countless art forms including some of the best known mystic symbols and religious motifs, and has a particularly rich history in Islamic architecture. It also provides a means of meditation and comtemplation, for example the study of the Kaballah Sefirot (Tree Of Life) and Metatron's Cube; and also the act of drawing itself.
The Dutch graphic designer M. C. Escher created mathematically inspired woodcuts, lithographs, and mezzotints. These feature impossible constructions, explorations of infinity, architecture, visual paradoxes and tessellations.
Some painters and sculptors create work distorted with the mathematical principles of anamorphosis, including South African sculptor Jonty Hurwitz.
British constructionist artist John Ernest created reliefs and paintings inspired by group theory.[29] A number of other British artists of the constructionist and systems schools of thought also draw on mathematics models and structures as a source of inspiration, including Anthony Hill and Peter Lowe.[30] Computer-generated art is based on mathematical algorithms.
Quotes by mathematicians
Bertrand Russell expressed his sense of mathematical beauty in these words:
Mathematics, rightly viewed, possesses not only truth, but supreme beauty—a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as poetry.[31]
Paul Erdős expressed his views on the ineffability of mathematics when he said, "Why are numbers beautiful? It's like asking why is Beethoven's Ninth Symphony beautiful. If you don't see why, someone can't tell you. I know numbers are beautiful. If they aren't beautiful, nothing is".[32]
See also
- Argument from beauty
- Cellular automaton
- Descriptive science
- Fluency heuristic
- Golden ratio
- Mathematics and architecture
- Neuroesthetics
- Normative science
- Philosophy of mathematics
- Processing fluency theory of aesthetic pleasure
- Pythagoreanism
- Theory of everything
Notes
- ↑ "Quotations by Hardy". https://www-history.mcs.st-andrews.ac.uk/Quotations/Hardy.html.
- ↑ Elisha Scott Loomis published over 360 proofs in his book Pythagorean Proposition (ISBN 0-873-53036-5).
- ↑ Weisstein, Eric W.. "Quadratic Reciprocity Theorem" (in en). http://mathworld.wolfram.com/QuadraticReciprocityTheorem.html.
- ↑ Rota (1997), p. 173.
- ↑ Gallagher, James (13 February 2014). "Mathematics: Why the brain sees maths as beauty". BBC News online. https://www.bbc.co.uk/news/science-environment-26151062.
- ↑ Feynman, Richard P. (1977). The Feynman Lectures on Physics. I. Addison-Wesley. ISBN 0-201-02010-6. https://feynmanlectures.caltech.edu/I_22.html#Ch22-S6-p4.
- ↑ Weisstein, Eric W.. "Fundamental Theorems of Calculus" (in en). http://mathworld.wolfram.com/FundamentalTheoremsofCalculus.html.
- ↑ Hardy, G.H.. "18". A Mathematician's Apology. https://archive.org/details/AMathematiciansApology-G.h.Hardy/page/n31/mode/2up.
- ↑ Rota (1997), p. 172.
- ↑ Monastyrsky (2001), Some Trends in Modern Mathematics and the Fields Medal
- ↑ Lang, p. 3
- ↑ Chandrasekhar, p. 148
- ↑ Phillips, George (2005). "Preface". Mathematics Is Not a Spectator Sport. Springer Science+Business Media. ISBN 0-387-25528-1. https://books.google.com/books?id=psFwdN6V6icC&q=there+is+nothing+in+the+world+of+mathematics+that+corresponds+to+an+audience+in+a+concert+hall,+where+the+passive+listen+to+the+active.+Happily,+mathematicians+are+all+doers,+not+spectators.&pg=PR7. Retrieved 2008-08-22. ""...there is nothing in the world of mathematics that corresponds to an audience in a concert hall, where the passive listen to the active. Happily, mathematicians are all doers, not spectators."
- ↑ Sowell, E (1989). "Effects of Manipulative Materials in Mathematics Instruction". Journal for Research in Mathematics Education 20 (5): 498–505. doi:10.2307/749423.
- ↑ Hull, Thomas. "Project Origami: Activities for Exploring Mathematics". Taylor & Francis, 2006.
- ↑ Brualdi, Richard (2009). Introductory Combinatorics. Pearson. ISBN 978-0136020400.
- ↑ Zeki, Semir; Romaya, John Paul; Benincasa, Dionigi M. T.; Atiyah, Michael F. (2014). "The experience of mathematical beauty and its neural correlates". Frontiers in Human Neuroscience 8: 68. doi:10.3389/fnhum.2014.00068. ISSN 1662-5161. PMID 24592230.
- ↑ Zhang, Haoxuan; Zeki, Semir (May 2022). "Judgments of mathematical beauty are resistant to revision through external opinion". PsyCh Journal 11 (5): 741–747. doi:10.1002/pchj.556. ISSN 2046-0252. PMID 35491015.
- ↑ Linnebo, Øystein (2018), Zalta, Edward N., ed., Platonism in the Philosophy of Mathematics (Spring 2018 ed.), Metaphysics Research Lab, Stanford University, https://plato.stanford.edu/archives/spr2018/entries/platonism-mathematics/, retrieved 2019-10-31
- ↑ Schechter, Bruce (2000). My brain is open: The mathematical journeys of Paul Erdős. New York: Simon & Schuster. pp. 70–71. ISBN 0-684-85980-7.
- ↑ "Alain Badiou: Ontology and Structuralism" (in en-US). 2014-04-02. https://ceasefiremagazine.co.uk/alain-badiou-ontology-structuralism/.
- ↑ A. Moles: Théorie de l'information et perception esthétique, Paris, Denoël, 1973 (Information Theory and aesthetical perception)
- ↑ F Nake (1974). Ästhetik als Informationsverarbeitung. (Aesthetics as information processing). Grundlagen und Anwendungen der Informatik im Bereich ästhetischer Produktion und Kritik. Springer, 1974, ISBN 3-211-81216-4, ISBN 978-3-211-81216-7
- ↑ J. Schmidhuber. Low-complexity art. Leonardo, Journal of the International Society for the Arts, Sciences, and Technology (Leonardo/ISAST), 30(2):97–103, 1997. doi:10.2307/1576418. JSTOR 1576418.
- ↑ J. Schmidhuber. Papers on the theory of beauty and low-complexity art since 1994: http://www.idsia.ch/~juergen/beauty.html
- ↑ J. Schmidhuber. Simple Algorithmic Principles of Discovery, Subjective Beauty, Selective Attention, Curiosity & Creativity. Proc. 10th Intl. Conf. on Discovery Science (DS 2007) pp. 26–38, LNAI 4755, Springer, 2007. Also in Proc. 18th Intl. Conf. on Algorithmic Learning Theory (ALT 2007) p. 32, LNAI 4754, Springer, 2007. Joint invited lecture for DS 2007 and ALT 2007, Sendai, Japan, 2007. arXiv:0709.0674.
- ↑ Schmidhuber, J. (1991). "Curious model-building control systems". International Joint Conference on Neural Networks. 2. Singapore: IEEE press. pp. 1458–1463. doi:10.1109/IJCNN.1991.170605.
- ↑ Schmidhuber's theory of beauty and curiosity in a German TV show: http://www.br-online.de/bayerisches-fernsehen/faszination-wissen/schoenheit--aesthetik-wahrnehmung-ID1212005092828.xml
- ↑ John Ernest's use of mathematics and especially group theory in his art works is analysed in John Ernest, A Mathematical Artist by Paul Ernest in Philosophy of Mathematics Education Journal, No. 24 Dec. 2009 (Special Issue on Mathematics and Art): http://people.exeter.ac.uk/PErnest/pome24/index.htm
- ↑ Franco, Francesca (2017-10-05). "The Systems Group (Chapter 2)" (in en). Generative Systems Art: The Work of Ernest Edmonds. Routledge. ISBN 9781317137436. https://books.google.com/books?id=oJU4DwAAQBAJ&q=anthony+hill+and+peter+lowe&pg=PT61.
- ↑ Russell, Bertrand (1919). "The Study of Mathematics". Mysticism and Logic: And Other Essays. Longman. p. 60. https://archive.org/details/bub_gb_zwMQAAAAYAAJ. Retrieved 2008-08-22. "Mathematics rightly viewed possesses not only truth but supreme beauty a beauty cold and austere like that of sculpture without appeal to any part of our weaker nature without the gorgeous trappings Russell."
- ↑ Devlin, Keith (2000). "Do Mathematicians Have Different Brains?". The Math Gene: How Mathematical Thinking Evolved And Why Numbers Are Like Gossip. Basic Books. p. 140. ISBN 978-0-465-01619-8. https://archive.org/details/mathgene00keit. Retrieved 2008-08-22.
References
- Aigner, Martin, and Ziegler, Gunter M. (2003), Proofs from THE BOOK, 3rd edition, Springer-Verlag.
- Chandrasekhar, Subrahmanyan (1987), Truth and Beauty: Aesthetics and Motivations in Science, University of Chicago Press, Chicago, IL.
- Hadamard, Jacques (1949), The Psychology of Invention in the Mathematical Field, 1st edition, Princeton University Press, Princeton, NJ. 2nd edition, 1949. Reprinted, Dover Publications, New York, NY, 1954.
- Hardy, G.H. (1940), A Mathematician's Apology, 1st published, 1940. Reprinted, C. P. Snow (foreword), 1967. Reprinted, Cambridge University Press, Cambridge, UK, 1992.
- Hoffman, Paul (1992), The Man Who Loved Only Numbers, Hyperion.
- Huntley, H.E. (1970), The Divine Proportion: A Study in Mathematical Beauty, Dover Publications, New York, NY.
- Lang, Serge (1985). The Beauty of Doing Mathematics: Three Public Dialogues. New York: Springer-Verlag. ISBN 0-387-96149-6.
- Loomis, Elisha Scott (1968), The Pythagorean Proposition, The National Council of Teachers of Mathematics. Contains 365 proofs of the Pythagorean Theorem.
- Monastyrsky, Michael (2001). "Some Trends in Modern Mathematics and the Fields Medal". Can. Math. Soc. Notes 33 (2 and 3). http://www.fields.utoronto.ca/aboutus/FieldsMedal_Monastyrsky.pdf.
- Pandey, S.K. . The Humming of Mathematics: Melody of Mathematics. Independently Published, 2019. ISBN:1710134437.
- Peitgen, H.-O., and Richter, P.H. (1986), The Beauty of Fractals, Springer-Verlag.
- Reber, R.; Brun, M.; Mitterndorfer, K. (2008). "The use of heuristics in intuitive mathematical judgment". Psychonomic Bulletin & Review 15 (6): 1174–1178. doi:10.3758/PBR.15.6.1174. PMID 19001586.
- Rota, Gian-Carlo (1997). "The phenomenology of mathematical beauty". Synthese 111 (2): 171–182. doi:10.1023/A:1004930722234.
- Strohmeier, John, and Westbrook, Peter (1999), Divine Harmony, The Life and Teachings of Pythagoras, Berkeley Hills Books, Berkeley, CA.
Further reading
- Cellucci, Carlo (2015), "Mathematical beauty, understanding, and discovery", Foundations of Science 20 (4): 339–355, doi:10.1007/s10699-014-9378-7
- Martin Gardner (April 1, 2007). "Is Beauty Truth and Truth Beauty?". Scientific American. https://www.scientificamerican.com/article/is-beauty-truth-and-truth/.
- Stewart, Ian (2007). Why beauty is truth : a history of symmetry. New York: Basic Books, a member of the Perseus Books Group. ISBN 978-0-465-08236-0. OCLC 76481488. https://www.worldcat.org/oclc/76481488.
- Zeki, S.; Romaya, J. P.; Benincasa, D. M. T.; Atiyah, M. F. (2014), "The experience of mathematical beauty and its neural correlates", Frontiers in Human Neuroscience 8: 68, doi:10.3389/fnhum.2014.00068, PMID 24592230
External links
- Mathematics, Poetry and Beauty
- Is Mathematics Beautiful? cut-the-knot.org
- Justin Mullins.com
- Edna St. Vincent Millay (poet): Euclid alone has looked on beauty bare
- Terence Tao, What is good mathematics?
- Mathbeauty Blog
- A Mathematical Romance Jim Holt December 5, 2013 issue of The New York Review of Books review of Love and Math: The Heart of Hidden Reality by Edward Frenkel
 |